新人教版九年级上册第24章圆的复习课件
文档属性
| 名称 | 新人教版九年级上册第24章圆的复习课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 259.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-19 00:00:00 | ||
图片预览




文档简介
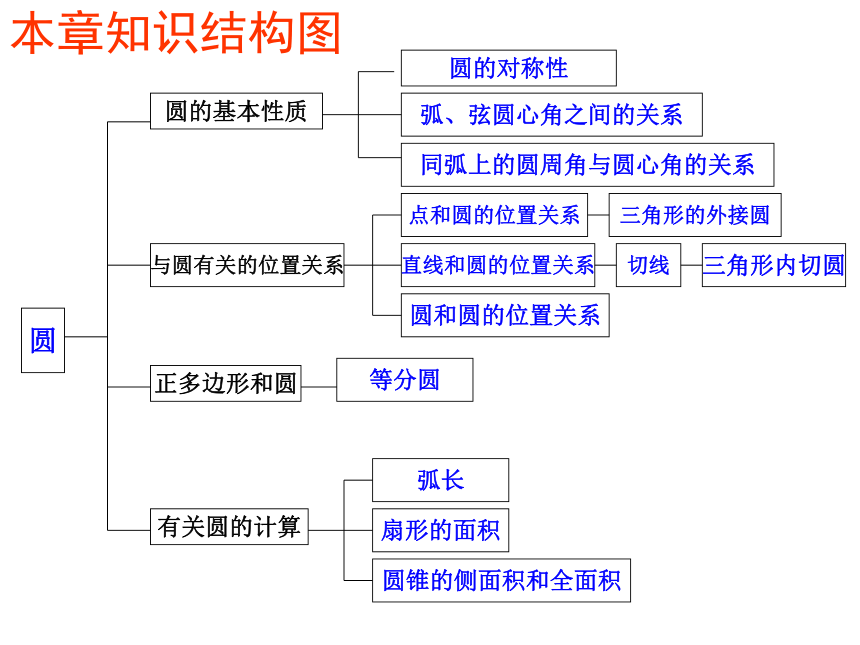
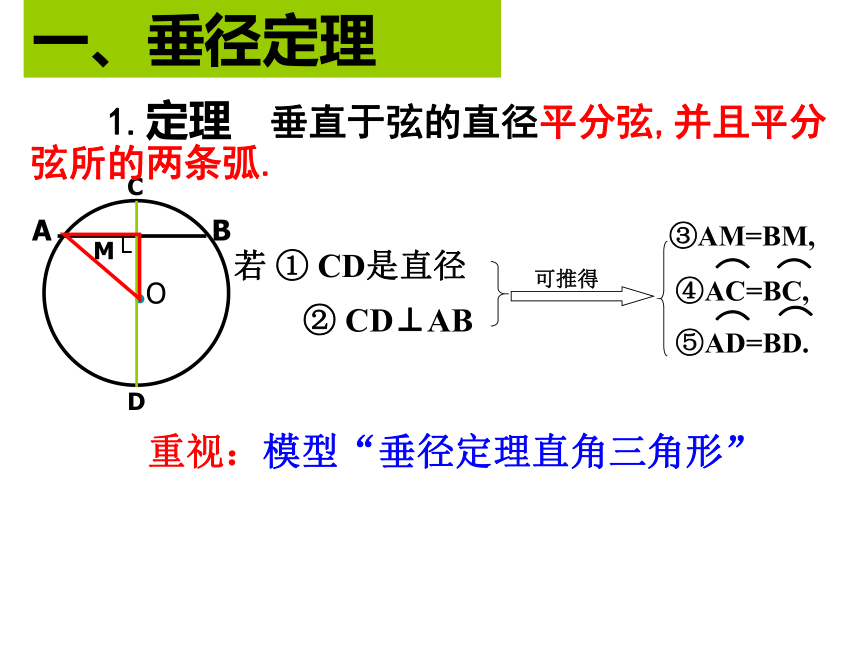
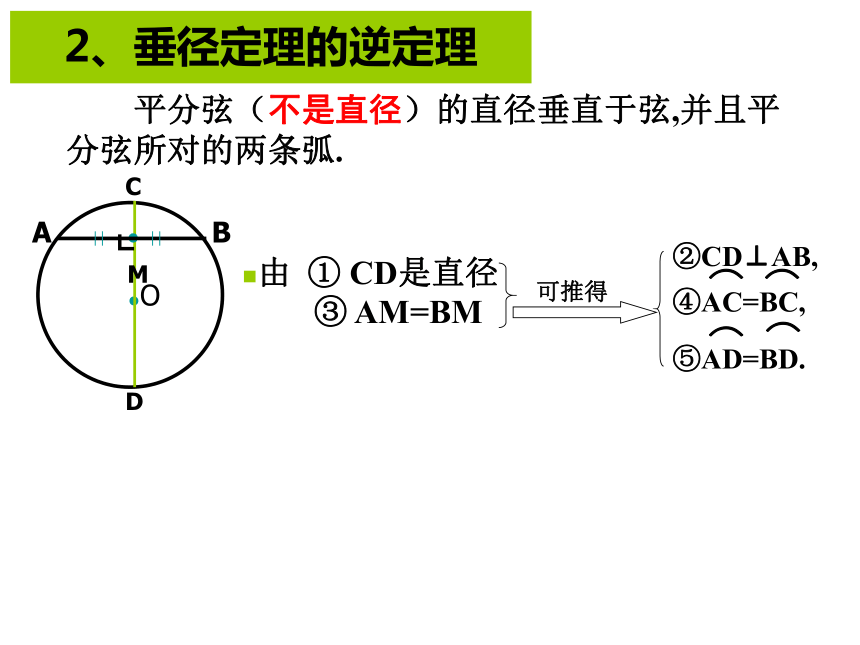
课件42张PPT。复习--圆本章知识结构图圆的基本性质圆圆的对称性弧、弦圆心角之间的关系同弧上的圆周角与圆心角的关系与圆有关的位置关系正多边形和圆有关圆的计算点和圆的位置关系切线直线和圆的位置关系三角形的外接圆三角形内切圆等分圆圆和圆的位置关系弧长扇形的面积圆锥的侧面积和全面积一、垂径定理③AM=BM,重视:模型“垂径定理直角三角形” 若 ① CD是直径② CD⊥AB 1.定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.2、垂径定理的逆定理 平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.垂径定理及推论直径 (过圆心的线);(2)垂直弦;
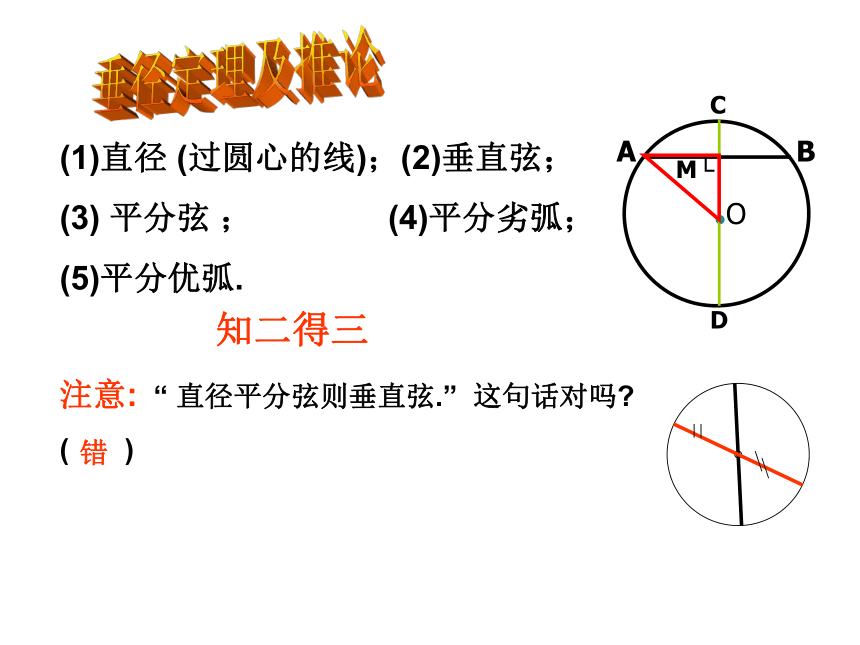
(3) 平分弦 ; (4)平分劣弧;
(5)平分优弧.知二得三注意: “ 直径平分弦则垂直弦.” 这句话对吗?
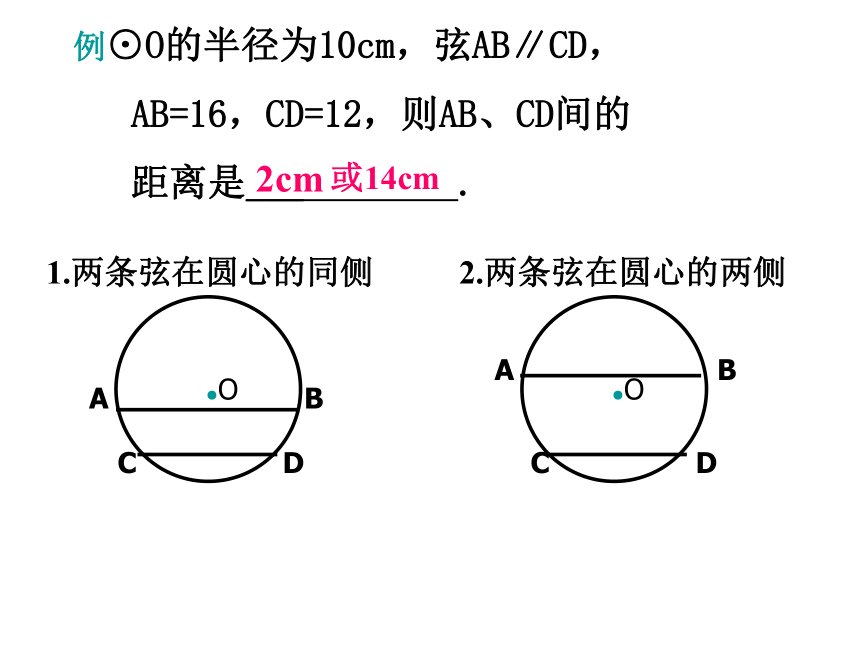
( )错例⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
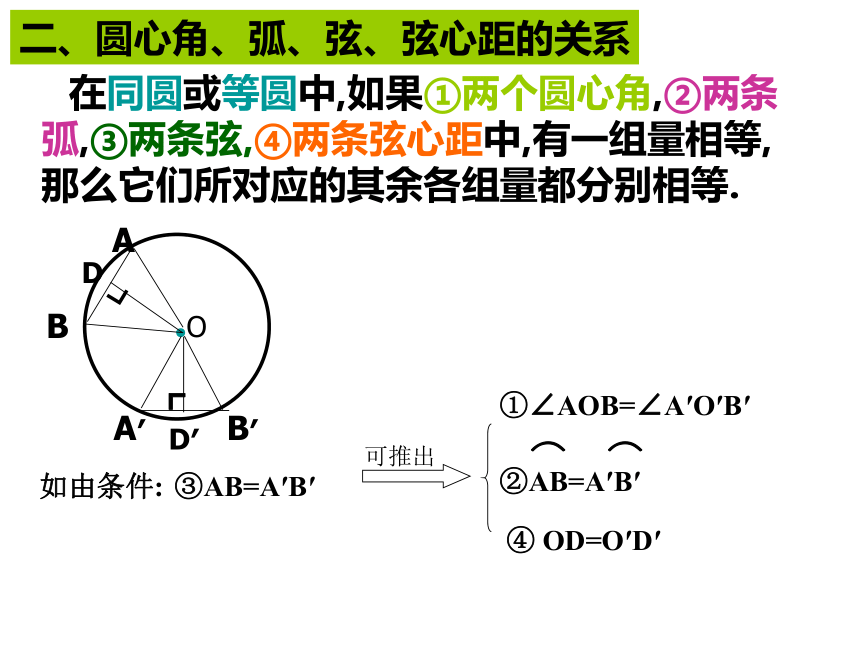
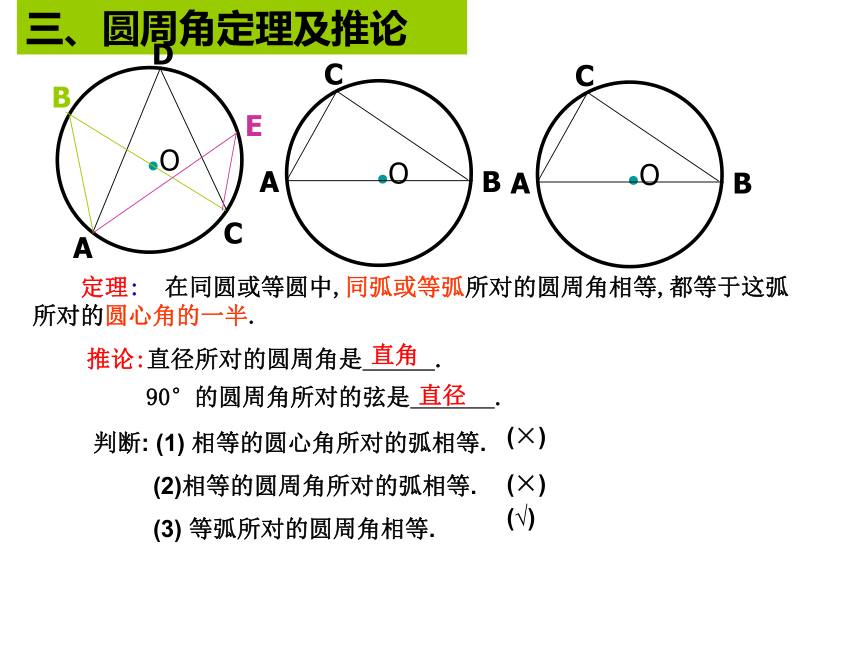
距离是___ .2cm或14cm 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′二、圆心角、弧、弦、弦心距的关系三、圆周角定理及推论 90°的圆周角所对的弦是 . 定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半. 推论:直径所对的圆周角是 .直角直径判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.(×)(×)(√) 1、如图1,AB是⊙O的直径,C为圆上一点,弧AC度数为60°,OD⊥BC,D为垂足,且OD=10,则AB=_____,BC=_____;
2、已知、是同圆的两段弧,且弧AB等于2倍弧AC,则弦AB与CD之间的关系为( );
A.AB=2CD B.AB<2CD C.AB>2CD D.不能确定
3、 如图2,⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( );
A.150° B.130° C.120° D.60°
4、在△ABC中,∠A=70°,若O为△ABC的外心,∠BOC= ;若O为△ABC的内心,∠BOC= .
图1 图2 1、两个同心圆的直径分别为5 cm和3 cm,则圆环部分的宽度为_____ cm;
2、如图1,已知⊙O,AB为直径,AB⊥CD,垂足为E,由图你还能知道哪些正确的结论?请把它们一一写出来 ;
3、为改善市区人民生活环境,市建设污水管网工程,某圆柱型水管的直径为100 cm,截面如图2,若管内污水的面宽AB=60 cm,则污水的最大深度为 cm;
4、已知、是同圆的两段弧,且=2,则弦AB与CD之间的关系为( ).A.AB=2CD;B.AB<2CD;C.AB>2CD;D.不能确定
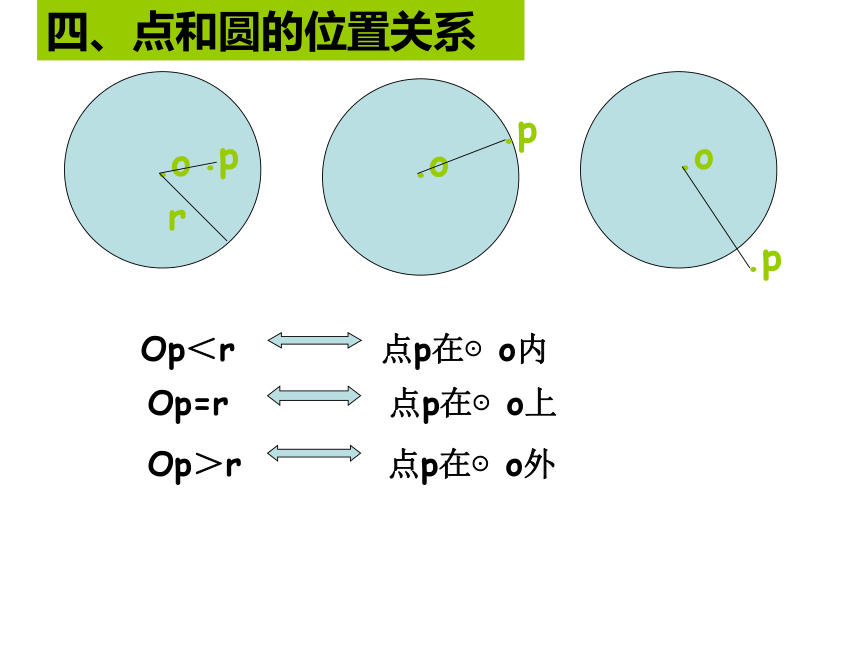
图1 图2四、点和圆的位置关系 不在同一直线上的三个点确定一个圆 (这个三角形叫做圆的内接三角形,这个圆叫做三角形的外接圆,圆心叫做三角形的外心)
圆内接四边形的性质:
(1)对角互补;(2)任意一个外角都等于它的内对角 反证法的三个步骤:
1、提出假设
2、由题设出发,引出矛盾
3、由矛盾判定假设不成立,肯定结论正确
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A、1∶2∶3∶4 B、1∶3∶2∶4
C、4∶2∶3∶1 D、4∶2∶1∶3
练:有两个同心圆,半径分别为R和r,
P是圆环内一点,则OP的取值
范围是_____.r切线的判定定理定理 经过半径的外端,并且垂直于这条半径的直线是圆的切线.CD●OA 如图
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.判定切线的方法:(1)定义(2)圆心到直线的距离d=圆的半径r(3)切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定定理的两种应用 1、如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.切线的性质定理圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径CD●OA∴CD⊥OA.切线的性质定理出可理解为 如果一条直线满足以下三个性质中的任意两个,那么
第三个也成立。①经过切点、②垂直于切线、③经过圆心。
如 ①
②③①
③②②
③①任意两个 1、两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC=_____ cm;
2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点,
设AB=12,则两圆构成圆环面积为_____;
3、下列四个命题中正确的是( ).
①与圆有公共点的直线是该圆的切线 ; ②垂直于圆的半径的直线是该圆的切线 ; ③到圆心的距离等于半径的直线是该圆的切线 ;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A.①② B.②③ C.③④ D.①④一、判断。
1、三角形的外心到三角形各边的距离相等; ( )
2、直角三角形的外心是斜边的中点. ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接
圆半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之比 .
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆×√6.5cm2cm2:1C四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.30cm交点个数 名称0外离1外切2相交1内切0内含同心圆是内含的特殊情况d , R , r 的关系dR rd > R + rd = R + rR-r< d < R+ rd = R - r0≤d < R - r六.圆与圆的位置关系ABCO七.三角形的外接圆和内切圆:ABCI三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.三角形的外心是否一定在三角形的内部?从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.切线长定理及其推论:∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2熟练掌握以下的结论rr1.如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.60度30或150度 2:已知ABC三点在圆O上,连接ABCO,如果∠ AOC=140 °,求∠ B的度数. 3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.D 解:在优弧AC上定一点D,连结AD、
CD.
∵ ∠ AOC=140 °
∴ ∠ D=70 °
∴ ∠ B=180 ° -70 ° =110 °2或4cm 4.怎样要将一个如图所示的破镜重圆?ABCP 5、 如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若 CP=7cm,AB=28cm ,你能帮老师求出这面镜子的半径吗?O714综合应用垂径定理和勾股定理可求得半径 6.如图:AB是圆O的直径,BD是圆O的弦,
BD到C,AC=AB,BD与CD的大小有什么关系?
为什么? 补充:
若∠B=70 °,则∠DOE=___.E40 ° 7、如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.一、圆的周长公式二、圆的面积公式C=2πrS=πr2三、弧长的计算公式四、扇形面积计算公式五 、大于半圆的弓形面积为S弓形=S扇形+S△六 、小于半圆的弓形面积为S弓形=S扇形-S△4.14.2圆锥的侧面积和全面积圆锥的底面周长就是其侧面展开图扇形的弧长,
圆锥的母线就是其侧面展开图扇形的半径。1、 扇形AOB的半径为12cm,∠AOB=120°,求扇形的面积和周长.2、 如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为______.A3:如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时,点A经过的路线长。4.如下图,所示的三角形铁皮余料,剪下扇形制成圆锥形玩具,已知∠C=90度,AB=BC=4cm,使剪下的扇形边缘半径在三角形边上,弧与其他边相切,设计裁剪的方案图,直接写出扇形的半径长。O
5、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是_________°.
240°6、 圆锥的母线为5cm,底面半径为3cm,则圆锥的表面积为_______24πcm27、已知:在RtΔABC,
求以AB为轴旋转一周所得到的几何体的全面积。分析:
以AB为轴旋转一周所得到的几何体是由公共底面的两个圆锥所组成的几何体,因此求全面积就是求两个圆锥的侧面积。8:如图,在Rt△ABC中,∠ACB=900。(1)分别以AC,BC为轴旋转一周所得的圆锥相同吗?(2)以AB为轴旋转一周得到怎样的几何体?(3)若AB=5,BC=4,你能求出题(2)中几何体的表面积吗?9.如图,圆锥的底面半径为2cm,母线长为8cm,一只蚂蚁从底面圆周上一点A出发,沿圆锥侧面爬行一周回到A点,求蚂蚁爬行的最短路线长是多少?B
(3) 平分弦 ; (4)平分劣弧;
(5)平分优弧.知二得三注意: “ 直径平分弦则垂直弦.” 这句话对吗?
( )错例⊙O的半径为10cm,弦AB∥CD,
AB=16,CD=12,则AB、CD间的
距离是___ .2cm或14cm 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′二、圆心角、弧、弦、弦心距的关系三、圆周角定理及推论 90°的圆周角所对的弦是 . 定理: 在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这弧所对的圆心角的一半. 推论:直径所对的圆周角是 .直角直径判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
(3) 等弧所对的圆周角相等.(×)(×)(√) 1、如图1,AB是⊙O的直径,C为圆上一点,弧AC度数为60°,OD⊥BC,D为垂足,且OD=10,则AB=_____,BC=_____;
2、已知、是同圆的两段弧,且弧AB等于2倍弧AC,则弦AB与CD之间的关系为( );
A.AB=2CD B.AB<2CD C.AB>2CD D.不能确定
3、 如图2,⊙O中弧AB的度数为60°,AC是⊙O的直径,那么∠BOC等于 ( );
A.150° B.130° C.120° D.60°
4、在△ABC中,∠A=70°,若O为△ABC的外心,∠BOC= ;若O为△ABC的内心,∠BOC= .
图1 图2 1、两个同心圆的直径分别为5 cm和3 cm,则圆环部分的宽度为_____ cm;
2、如图1,已知⊙O,AB为直径,AB⊥CD,垂足为E,由图你还能知道哪些正确的结论?请把它们一一写出来 ;
3、为改善市区人民生活环境,市建设污水管网工程,某圆柱型水管的直径为100 cm,截面如图2,若管内污水的面宽AB=60 cm,则污水的最大深度为 cm;
4、已知、是同圆的两段弧,且=2,则弦AB与CD之间的关系为( ).A.AB=2CD;B.AB<2CD;C.AB>2CD;D.不能确定
图1 图2四、点和圆的位置关系 不在同一直线上的三个点确定一个圆 (这个三角形叫做圆的内接三角形,这个圆叫做三角形的外接圆,圆心叫做三角形的外心)
圆内接四边形的性质:
(1)对角互补;(2)任意一个外角都等于它的内对角 反证法的三个步骤:
1、提出假设
2、由题设出发,引出矛盾
3、由矛盾判定假设不成立,肯定结论正确
1、⊙O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与⊙O的位置关系是( )
A.点A在⊙O内部 B.点A在⊙O上
C.点A在⊙O外部 D.点A不在⊙O上
2、M是⊙O内一点,已知过点M的⊙O最长的弦为10 cm,最短的弦长为8 cm,则OM=?_____ cm.?
3、圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是( )
A、1∶2∶3∶4 B、1∶3∶2∶4
C、4∶2∶3∶1 D、4∶2∶1∶3
练:有两个同心圆,半径分别为R和r,
P是圆环内一点,则OP的取值
范围是_____.r
∵OA是⊙O的半径, 且CD⊥OA,
∴ CD是⊙O的切线.判定切线的方法:(1)定义(2)圆心到直线的距离d=圆的半径r(3)切线的判定定理:经过半径的外端,并且垂直于这条半径的直线是圆的切线.
切线的判定定理的两种应用 1、如果已知直线与圆有交点,往往要作出过这一点的半径,再证明直线垂直于这条半径即可;
2、如果不明确直线与圆的交点,往往要作出圆心到直线的垂线段,再证明这条垂线段等于半径即可.切线的性质定理圆的切线垂直于过切点的半径.
∵CD切⊙O于A, OA是⊙O的半径CD●OA∴CD⊥OA.切线的性质定理出可理解为 如果一条直线满足以下三个性质中的任意两个,那么
第三个也成立。①经过切点、②垂直于切线、③经过圆心。
如 ①
②③①
③②②
③①任意两个 1、两个同心圆的半径分别为3 cm和4 cm,大圆的弦BC与小圆相切,则BC=_____ cm;
2、如图2,在以O为圆心的两个同心圆
中,大圆的弦AB是小圆的切线,P为切点,
设AB=12,则两圆构成圆环面积为_____;
3、下列四个命题中正确的是( ).
①与圆有公共点的直线是该圆的切线 ; ②垂直于圆的半径的直线是该圆的切线 ; ③到圆心的距离等于半径的直线是该圆的切线 ;④过圆直径的端点,垂直于此直径的直线是该圆的切线.
A.①② B.②③ C.③④ D.①④一、判断。
1、三角形的外心到三角形各边的距离相等; ( )
2、直角三角形的外心是斜边的中点. ( )
二、填空:
1、直角三角形的两条直角边分别是5cm和12cm,则它的外接
圆半径 ,内切圆半径 ;
2、等边三角形外接圆半径与内切圆半径之比 .
三、选择题:
下列命题正确的是( )
A、三角形外心到三边距离相等
B、三角形的内心不一定在三角形的内部
C、等边三角形的内心、外心重合
D、三角形一定有一个外切圆×√6.5cm2cm2:1C四、一个三角形,它的周长为30cm,它的内切圆半径为2cm,则这个三角形的面积为______.30cm交点个数 名称0外离1外切2相交1内切0内含同心圆是内含的特殊情况d , R , r 的关系dR rd > R + rd = R + rR-r< d < R+ rd = R - r0≤d < R - r六.圆与圆的位置关系ABCO七.三角形的外接圆和内切圆:ABCI三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.三角形的外心是否一定在三角形的内部?从圆外一点向圆所引的两条切线长相等;并且这一点和圆心的连线平分两条切线的夹角.切线长定理及其推论:∵PA,PB切⊙O于A,B
∴PA=PB ∠1=∠2熟练掌握以下的结论rr1.如图:圆O中弦AB等于半径R,则这条弦所对的圆心角是___,圆周角是______.60度30或150度 2:已知ABC三点在圆O上,连接ABCO,如果∠ AOC=140 °,求∠ B的度数. 3.平面上一点P到圆O上一点的距离最长为6cm,最短为2cm,则圆O的半径为_______.D 解:在优弧AC上定一点D,连结AD、
CD.
∵ ∠ AOC=140 °
∴ ∠ D=70 °
∴ ∠ B=180 ° -70 ° =110 °2或4cm 4.怎样要将一个如图所示的破镜重圆?ABCP 5、 如图,AB是⊙O的任意一条弦,OC⊥AB,垂足为P,若 CP=7cm,AB=28cm ,你能帮老师求出这面镜子的半径吗?O714综合应用垂径定理和勾股定理可求得半径 6.如图:AB是圆O的直径,BD是圆O的弦,
BD到C,AC=AB,BD与CD的大小有什么关系?
为什么? 补充:
若∠B=70 °,则∠DOE=___.E40 ° 7、如图,AB是圆O的直径,圆O过AC的中点D,DE⊥BC于E.
证明:DE是圆O的切线.一、圆的周长公式二、圆的面积公式C=2πrS=πr2三、弧长的计算公式四、扇形面积计算公式五 、大于半圆的弓形面积为S弓形=S扇形+S△六 、小于半圆的弓形面积为S弓形=S扇形-S△4.14.2圆锥的侧面积和全面积圆锥的底面周长就是其侧面展开图扇形的弧长,
圆锥的母线就是其侧面展开图扇形的半径。1、 扇形AOB的半径为12cm,∠AOB=120°,求扇形的面积和周长.2、 如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为______.A3:如图,把Rt△ABC的斜边放在直线 上,按顺时针方向转动一次,使它转到 的位置。若BC=1,∠A=300。求点A运动到A′位置时,点A经过的路线长。4.如下图,所示的三角形铁皮余料,剪下扇形制成圆锥形玩具,已知∠C=90度,AB=BC=4cm,使剪下的扇形边缘半径在三角形边上,弧与其他边相切,设计裁剪的方案图,直接写出扇形的半径长。O
5、扇形的面积是它所在圆的面积的 ,这个扇
形的圆心角的度数是_________°.
240°6、 圆锥的母线为5cm,底面半径为3cm,则圆锥的表面积为_______24πcm27、已知:在RtΔABC,
求以AB为轴旋转一周所得到的几何体的全面积。分析:
以AB为轴旋转一周所得到的几何体是由公共底面的两个圆锥所组成的几何体,因此求全面积就是求两个圆锥的侧面积。8:如图,在Rt△ABC中,∠ACB=900。(1)分别以AC,BC为轴旋转一周所得的圆锥相同吗?(2)以AB为轴旋转一周得到怎样的几何体?(3)若AB=5,BC=4,你能求出题(2)中几何体的表面积吗?9.如图,圆锥的底面半径为2cm,母线长为8cm,一只蚂蚁从底面圆周上一点A出发,沿圆锥侧面爬行一周回到A点,求蚂蚁爬行的最短路线长是多少?B
同课章节目录
