旋转
图片预览










文档简介
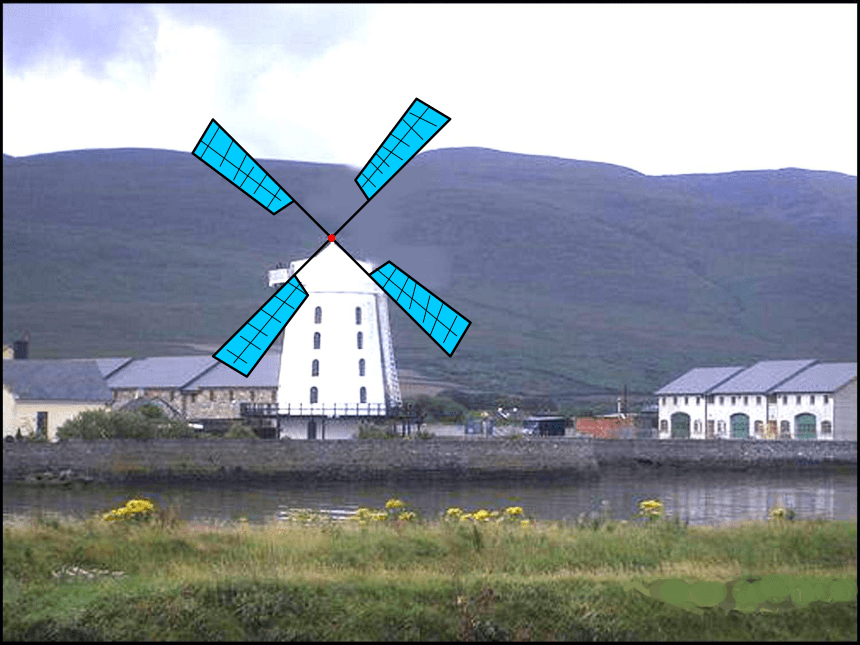
课件46张PPT。111第二十三章 旋转新疆的风车田游乐场的摩天轮夜光下的摩天轮夜光下的摩天轮从卫星拍摄到的台风“桑美”的中心旋涡美丽的图案观察:以上现象有什么共同特点?O图形的旋转
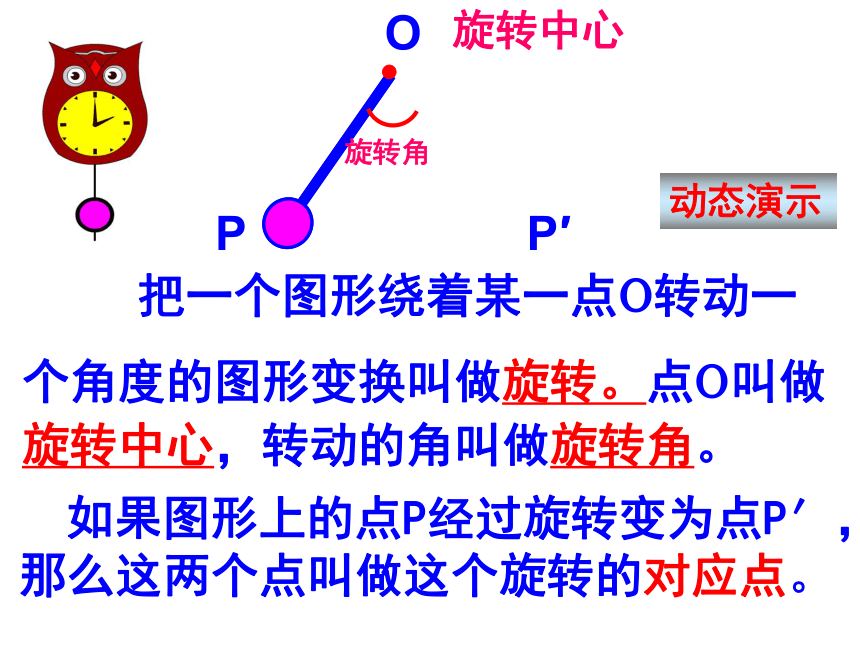
把一个图形绕着某一点o转动一个角度的图形变换叫做旋转。点o叫做旋转中心,转动的角叫做旋转角。 如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
O动态演示旋转中心旋转角生活中的旋转动态演示观察生活ABOA′B′动态演示1.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?学以致用OAB动态演示2.如图,△OAB绕点O旋转得
到△OA’B’,则:学以致用ABCO线段OA与OA′有什么关系?
∠AOA′与∠BOB′有什么关系?
△ABC与△A′B′C′形状和大小有什么关系?动态演示实验探究探究:旋转的基本性质 在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A/B/C/),移开硬纸板.
线段OA与OA/有什么关系?∠AOA/与∠BOB/有什么关系? △ABC与△A/B/ C/形状和大小有什么关系?活动二:· A/B/C/标出对应点同理 OB=OB/ 、 OC=OC/1、线段OA与OA/有什么关系?2、∠AOA/与∠BOB/有什么关系? 同理∠BOB/ = ∠COC/ 3、△ABC与△A/B/ C/形状和大小有什么关系?1、操作2、探究: △ABC≌ △ A/B/ C/连接对应点与
旋转中心OA=OA/∠AOA/=∠BOB/(1)对应点到旋转中心的距离_____.旋转的基本性质(3)旋转前、后的图形_____.(2)对应点与旋转中心所连线段的 夹角等于______ .3、归纳、概括相等旋转角全等 如图,如果把钟表的指针看做四边形AOBC,它绕点O顺时针旋转一定角度得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?旋转中心是点O点D和点E的位置AO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEF议一议:讨论 在图中,正方形ABCD与正方形EFGH边长
相等。这个图案可以看作是哪个“基本图案”通过
旋转得到的?ABCDEFGHOOABCDEFGH由正方形ABCD旋转45。
前后的图形共同组成ABC由△ABC分别旋转45。、
90。、135。、180。、225。,
前后的所有图形共同组成。由△AOB绕点O分别旋转45°、90°、135°、180°、225°、270°、315°前后的所有图形
共同组成ABO.下图是由正方形ABCD旋转而成。(1)旋转中心是_____
(2) 旋转的角度是____试一试点A450(3) 若正方形的边长是1,则C’D=_________C'D'B'BACD 下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 随堂练习1 香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?随堂练习2. 如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个. 随堂练习3.利用旋转来解决数学问题例题1.如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。析:关键是确定△ADE三个顶点的对应点,即它们旋转后的图形。解:因为点A是旋转中心,所以它的对应点是它 本身正方形ABCD中,AD=AB,∠DAB=90°,所以旋 转后点D与点B重合,设点E的对应点为点E’,因 为旋转后的图形与旋转前的图形全等,所以∠ ABE’ =∠ADE=90°, BE’= DE 因此,在CB的延长线上取点E’,使BE’= DE,则三角形ABE’为旋转后的图形。1.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。BAO⑴.连接OA⑵.作∠AOC=100°,在OC上截取OA’=OA⑷.作∠BOD=100°,在OD上截取OB’=OB⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。CD⑶.连接OB注:作旋转后的图形可以转化为作旋转后的对应点2.如图:画出△ABC绕点C按顺时针
方向旋转120°
后的对应的三角形。AB变式练习 练习 1.已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积..如图:△ABC是等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置 。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB上
中点,那么经过上述
的旋转后,点M到了
什么位置? 解:(1)旋转中心是A; (2)旋转了60度; (3)点M转到了AC的中点位置上.练习2. 如图:P是等边?ABC内的一点,把?ABP按不同的方向通过旋转得到?BQC和?ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ?ACR是否可以直接通过把?BQC旋转得到?练习3.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.◆什么叫图形的旋转?◆图形旋转的性质是什么?在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.1.旋转前、后的图形全等. 2.对应点到旋转中心的距离相等. 3每一对对应点与旋转中心的连线所成的角彼此相等. ◆图形的旋转是由旋转中心和旋转的角度决定. 课堂小结ABCDEF 2、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.找旋转中心旋转中心在对应点连线的垂直平分线上。练习.如图,将点阵中的图形绕点O按逆时针方向旋转900,画出旋转后的图形.
·2.在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度.A/B/C/3.已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长. 1.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得的, ①请你在图中用字母O标注出这一点;
②每次旋转了_______度;
③一共旋转了_______次..O605课堂练习 2.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?答:4次动动脑筋 4.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点...PP'课堂练习 5.如图,用左面的三角形经过怎样旋转,可以得到右面的图形. 6.找出图中扳手拧螺母时的旋转中心和旋转角..o ...ABC 解:图示,以O为旋转中心,第一次顺时针旋转120度,第二次顺时针旋转240度得到.课堂练习◆什么叫图形的旋转? 在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.◆图形旋转的性质是什么? 1.对应点到旋转中心的距离相等. 2.对应点与旋转中心所连线段的夹角等于旋转角. 3.旋转前、后的图形全等.
◆说说描述“旋转”的过程要注意哪几方面?
图形旋转时,必须注意旋转中心、旋转的角度和旋转的方向。
课堂小结布置作业:1、必做题:P80 习题 1、2
2、思考题:
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB,△COD是能够重合的图形。
求:(1)旋转中心,
(2)旋转角度数,
(3)图中经过旋转后能重合的三角形共有几对?若A、O、
C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度
自我反思这节课你学到了什么?
还有什么疑惑和建议?
把一个图形绕着某一点o转动一个角度的图形变换叫做旋转。点o叫做旋转中心,转动的角叫做旋转角。 如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
O动态演示旋转中心旋转角生活中的旋转动态演示观察生活ABOA′B′动态演示1.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?学以致用OAB动态演示2.如图,△OAB绕点O旋转得
到△OA’B’,则:学以致用ABCO线段OA与OA′有什么关系?
∠AOA′与∠BOB′有什么关系?
△ABC与△A′B′C′形状和大小有什么关系?动态演示实验探究探究:旋转的基本性质 在硬纸板上,挖一个三角形洞,再挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△A/B/C/),移开硬纸板.
线段OA与OA/有什么关系?∠AOA/与∠BOB/有什么关系? △ABC与△A/B/ C/形状和大小有什么关系?活动二:· A/B/C/标出对应点同理 OB=OB/ 、 OC=OC/1、线段OA与OA/有什么关系?2、∠AOA/与∠BOB/有什么关系? 同理∠BOB/ = ∠COC/ 3、△ABC与△A/B/ C/形状和大小有什么关系?1、操作2、探究: △ABC≌ △ A/B/ C/连接对应点与
旋转中心OA=OA/∠AOA/=∠BOB/(1)对应点到旋转中心的距离_____.旋转的基本性质(3)旋转前、后的图形_____.(2)对应点与旋转中心所连线段的 夹角等于______ .3、归纳、概括相等旋转角全等 如图,如果把钟表的指针看做四边形AOBC,它绕点O顺时针旋转一定角度得到四边形DOEF. 在这个旋转过程中:
(1)旋转中心是什么?
(2)经过旋转,点A、B分别移动到什么位置?
(3)旋转角是什么?
(4)AO与DO的长有什么关系?BO与EO呢?
(5)∠AOD与∠BOE有什么大小关系?旋转中心是点O点D和点E的位置AO=DO,BO=EO∠AOD=∠BOE∠AOD和∠BOE都是旋转角BACODEF议一议:讨论 在图中,正方形ABCD与正方形EFGH边长
相等。这个图案可以看作是哪个“基本图案”通过
旋转得到的?ABCDEFGHOOABCDEFGH由正方形ABCD旋转45。
前后的图形共同组成ABC由△ABC分别旋转45。、
90。、135。、180。、225。,
前后的所有图形共同组成。由△AOB绕点O分别旋转45°、90°、135°、180°、225°、270°、315°前后的所有图形
共同组成ABO.下图是由正方形ABCD旋转而成。(1)旋转中心是_____
(2) 旋转的角度是____试一试点A450(3) 若正方形的边长是1,则C’D=_________C'D'B'BACD 下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5 随堂练习1 香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?随堂练习2. 如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个. 随堂练习3.利用旋转来解决数学问题例题1.如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形。析:关键是确定△ADE三个顶点的对应点,即它们旋转后的图形。解:因为点A是旋转中心,所以它的对应点是它 本身正方形ABCD中,AD=AB,∠DAB=90°,所以旋 转后点D与点B重合,设点E的对应点为点E’,因 为旋转后的图形与旋转前的图形全等,所以∠ ABE’ =∠ADE=90°, BE’= DE 因此,在CB的延长线上取点E’,使BE’= DE,则三角形ABE’为旋转后的图形。1.已知线段AB和点O,画出AB绕点O逆时针旋转100°后的图形。BAO⑴.连接OA⑵.作∠AOC=100°,在OC上截取OA’=OA⑷.作∠BOD=100°,在OD上截取OB’=OB⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。CD⑶.连接OB注:作旋转后的图形可以转化为作旋转后的对应点2.如图:画出△ABC绕点C按顺时针
方向旋转120°
后的对应的三角形。AB变式练习 练习 1.已知,如图正方形EFOG绕与之边长相等的正方形ABCD的中心O旋转任意角度,求图中阴影部分的面积..如图:△ABC是等边三角形,D是BC边上的一点,△ABD经过旋转后到达△ACE的位置 。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果M是AB上
中点,那么经过上述
的旋转后,点M到了
什么位置? 解:(1)旋转中心是A; (2)旋转了60度; (3)点M转到了AC的中点位置上.练习2. 如图:P是等边?ABC内的一点,把?ABP按不同的方向通过旋转得到?BQC和?ACR,
(1)指出旋转中心、旋转方向和旋转角度?
(2) ?ACR是否可以直接通过把?BQC旋转得到?练习3.如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.◆什么叫图形的旋转?◆图形旋转的性质是什么?在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.1.旋转前、后的图形全等. 2.对应点到旋转中心的距离相等. 3每一对对应点与旋转中心的连线所成的角彼此相等. ◆图形的旋转是由旋转中心和旋转的角度决定. 课堂小结ABCDEF 2、如图,ΔDEF是由△ABC绕某一中心旋转一定的角度得到,请你找出这旋转中心.找旋转中心旋转中心在对应点连线的垂直平分线上。练习.如图,将点阵中的图形绕点O按逆时针方向旋转900,画出旋转后的图形.
·2.在等腰直角△ABC中,∠C=900,BC=2cm,如果以AC的中点O为旋转中心,将这个三角形旋转1800,点B落在点B′处,求BB′的长度.A/B/C/3.已知:如图,在△ABC中,∠BAC=1200,以BC为边向形外作等边三角形△BCD,把△ABD绕着点D按顺时针方向旋转600后得到△ECD,若AB=3,AC=2,求∠BAD的度数与AD的长. 1.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得的, ①请你在图中用字母O标注出这一点;
②每次旋转了_______度;
③一共旋转了_______次..O605课堂练习 2.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它是由其中一瓣经过几次旋转得到的?答:4次动动脑筋 4.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点...PP'课堂练习 5.如图,用左面的三角形经过怎样旋转,可以得到右面的图形. 6.找出图中扳手拧螺母时的旋转中心和旋转角..o ...ABC 解:图示,以O为旋转中心,第一次顺时针旋转120度,第二次顺时针旋转240度得到.课堂练习◆什么叫图形的旋转? 在平面内,将一个图形绕一个定点旋转一定的角度,这样的图形运动叫做图形的旋转.这个定点叫旋转中心.旋转的角度称为旋转角.◆图形旋转的性质是什么? 1.对应点到旋转中心的距离相等. 2.对应点与旋转中心所连线段的夹角等于旋转角. 3.旋转前、后的图形全等.
◆说说描述“旋转”的过程要注意哪几方面?
图形旋转时,必须注意旋转中心、旋转的角度和旋转的方向。
课堂小结布置作业:1、必做题:P80 习题 1、2
2、思考题:
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB,△COD是能够重合的图形。
求:(1)旋转中心,
(2)旋转角度数,
(3)图中经过旋转后能重合的三角形共有几对?若A、O、
C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度
自我反思这节课你学到了什么?
还有什么疑惑和建议?
同课章节目录
