关于原点对称的点的坐标
图片预览




文档简介
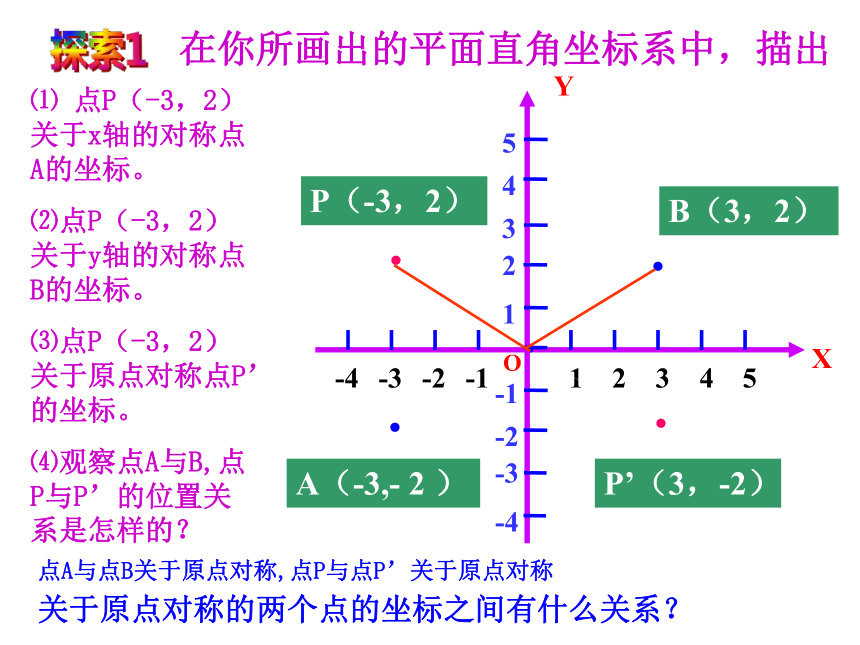
课件28张PPT。23.2.3关于原点对称的点的坐标B(3,2)·P(-3,2)A(-3,- 2 ) ··⑴ 点P(-3,2)关于x轴的对称点A的坐标。
⑵点P(-3,2)关于y轴的对称点B的坐标。
⑶点P(-3,2)关于原点对称点P’的坐标。
⑷观察点A与B,点P与P’的位置关系是怎样的?点A与点B关于原点对称,点P与点P’关于原点对称·在你所画出的平面直角坐标系中,描出P’(3,-2)关于原点对称的两个点的坐标之间有什么关系?探索1小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点(x, y)关于x轴对称的点的坐标为______.
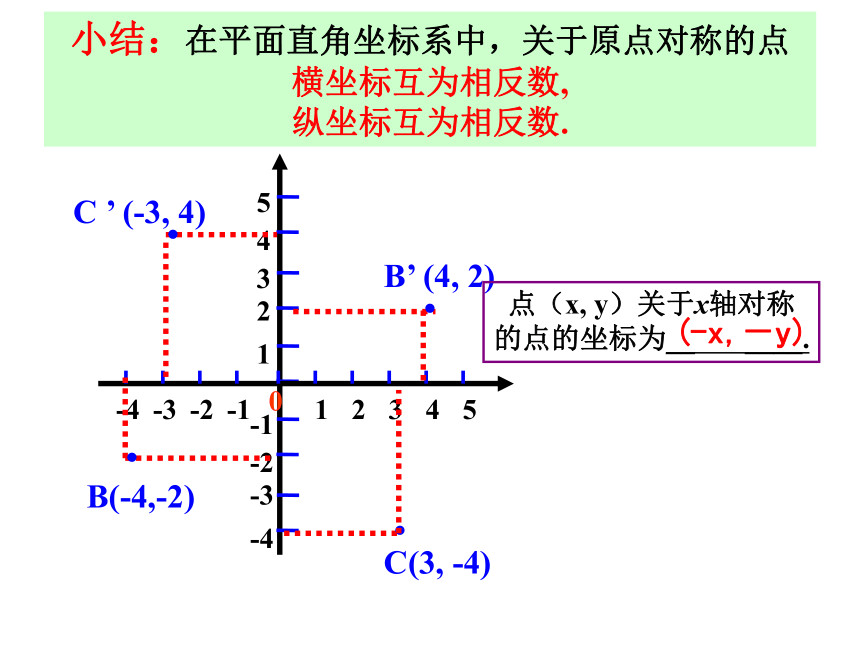
点(x, y)关于y轴对称的点的坐标为______.(x,-y)(-x,y)在平面直角坐标系中画出下列各点关于y轴的对称点.C ’ (-3, 4)··C(3, -4)·B’ (4, 2)·B(-4,-2)小结:在平面直角坐标系中,关于原点对称的点
横坐标互为相反数,
纵坐标互为相反数.点(x, y)关于x轴对称
的点的坐标为__ ____.(-x,-y)检验一下你的学习效果:
⒈点A(-1,3)关于原点对称的点的坐标是___________。
⒉点B(-3,0)关于原点对称的点的坐标是____________。
⒊点C(-x,y)关于原点对称的点的坐标是____________。
⒋若点A(m,-2),B(1,n)关于原点对称,则m=_____,n=_____。
⒌已知点P(x,y),xy>0,则点P关于原点的对称点在( )。
①第一象限 ②第三象限
③第一象限或第三象限 ④第二象限或第四象限
⒍已知点P(k,3),在直线y=x上,则点P关于原点对称的点的坐标是______________。
⒎下列各点中哪两个点关于原点对称?___________________。
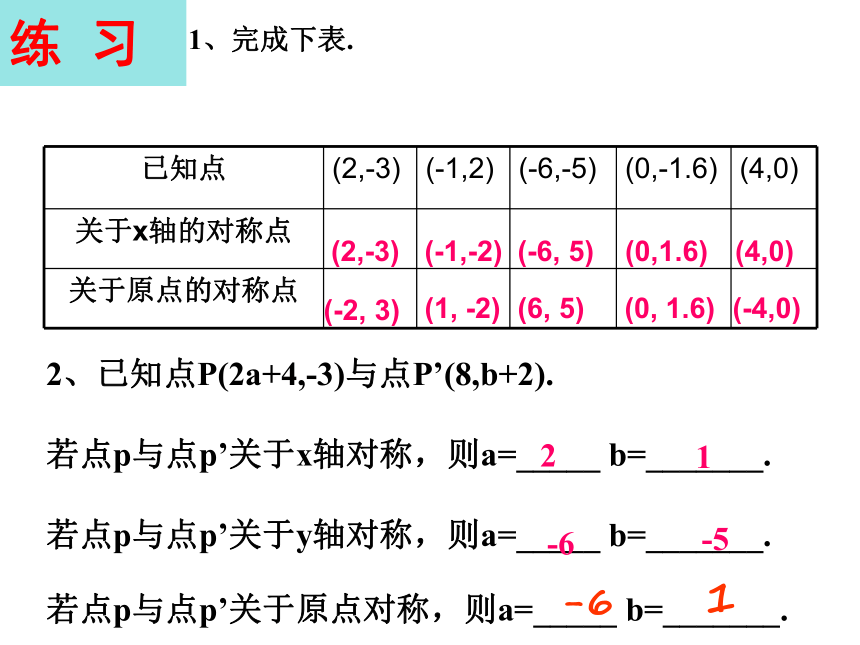
A(-5,0), B(0,2), C(2,-1), D(2,0), E(0,5) F(-2,1) G(-2,-1)-12(1,-3)(3,0)(x,-y)③(-3,-3)点C(2,-1)与F(-2,1)1、完成下表.
(-2, 3)(2,-3)(-1,-2)(1, -2)(6, 5)(-6, 5)(0, 1.6)(0,1.6)(-4,0)(4,0)2、已知点P(2a+4,-3)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
若点p与点p’关于原点对称,则a=_____ b=_______.练 习1-6-52-613.下列图象中,一定关于原点对称的图象是( )
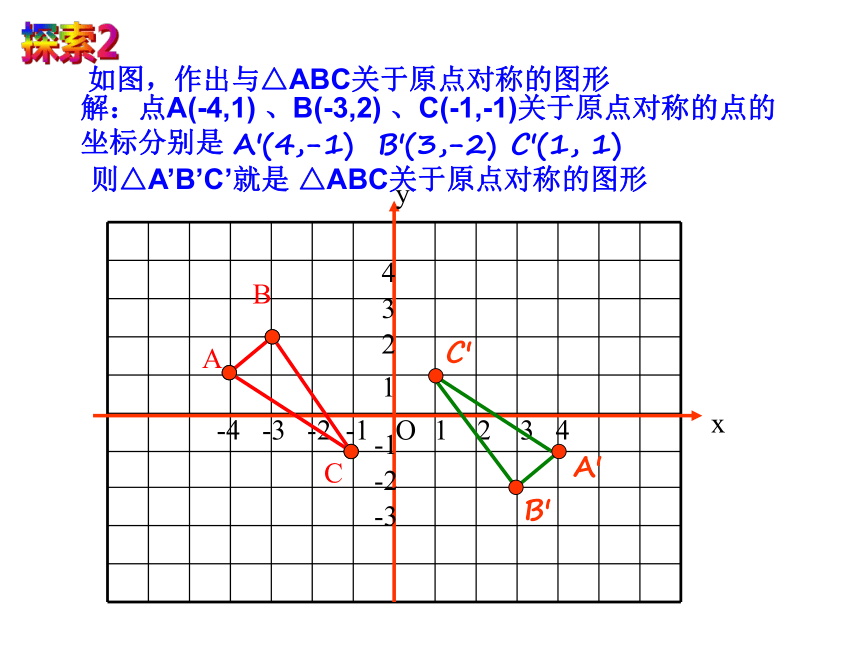
A.y=1/x B.y=2x+1 C.y=-2x+1 D.以上三种都有可能.如图,作出与△ABC关于原点对称的图形xyO-4 -3 -2 -1 1 2 3 4-12341-2-3A解:点A(-4,1) 、B(-3,2) 、C(-1,-1)关于原点对称的点的坐标分别是BC探索2A′B′C′则△A’B’C’就是 △ABC关于原点对称的图形
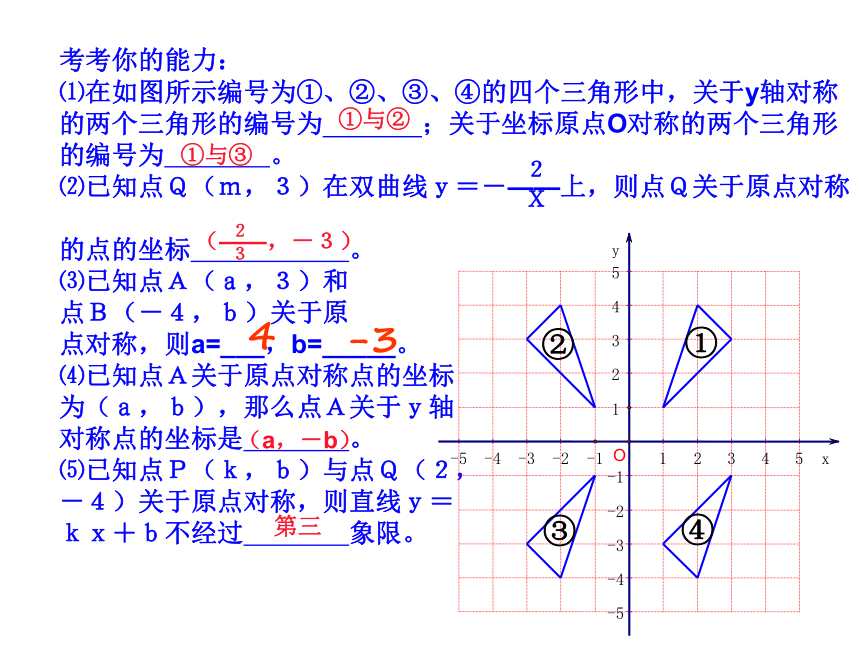
考考你的能力:
⑴在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为 。
⑵已知点Q(m,3)在双曲线y=-——上,则点Q关于原点对称
的点的坐标 。
⑶已知点A(a,3)和
点B(-4,b)关于原
点对称,则a=___,b=_____。
⑷已知点A关于原点对称点的坐标
为(a,b),那么点A关于y轴
对称点的坐标是 。
⑸已知点P(k,b)与点Q(2,
-4)关于原点对称,则直线y=
kx+b不经过 象限。
①与②①与③(a,-b)第三4-3xyO -5 -4 -3 -2 -1 1 2 3 4 5-12341-2-3 四边形ABCD各顶点的坐标分别为A(5,0),B(-2,3), C(-1,0), D(-1,-5),作出与四边形ABCD关于原点O对称的图形-4-55ABCD 平行四边形,A(1,2), B(-4,2), C(-2,-5),求出第四个点D的坐标.若平行四边形在坐标系内关于原点对称,已知点A,点B的坐标不变,点C,点D的坐标又是什么?拓 展 练 习1.如图 :在平面直角坐标系中A.B坐标分别为(2,0),(-1,3)。若△OAC与△OAB全等,试尽可能多的写出点C的坐标。3-121-103-31yxBAC3C2C12、(2008河南)如图,阴影部分组成的图案 既是关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),则点M 和点N 的坐标分别是:M(-1,-3)N(1,-3)3、如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转90°得到直线A1B1.
(1)在图中画出直线A1B1.
(2)求出经过线段A1B1中点C的反比例函数解析式.
(3)是否存在另一条与直线AB平行的直线y=kx+b,它与双曲线只有一个交点,若存在,求此直线的函数解析式,若不存在,请说明理由.4.如图,在平面直角坐标系中, △ABC为等边三角形,其中点A,B,C的坐标分别为(-3,-1),(-3,-3),(-3+√3,-2),现以Y轴为对称轴作△ ABC的对称图形,得△ A1B1C1,再以X轴为对称轴作△ A1B1C1的对称图形,得△ A2B2C2.(1).直接写出C1,C2的坐标.(2).能否通过一次旋转将△ ABC旋转到△ A2B2C2的位置?你若认为能, 请出肯定的回答,你若认为不能请作出否定的回答(不必说明理由).(3).设当△ ABC的位置发生变化时, △ A2B2C2., △ A1B1C1与△ ABC之间的对称关系始终保持不变.
①当△ ABC向上平移多少个单位时, △ A1B1C1与△ A2B2C2完全重合?并直接写出此时C点的坐标.
②将△ ABC绕点A顺时针旋转多少度,使△ A1B1C1与△ A2B2C2重合,点C的坐标又是什么?
1、会求已知点关于原点对称的 点的坐标。
2、会利用坐标画出关于原点对称的图形。
探究3:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗?x=1······P(-2,3)M(-1,1)N’(5,-2)N(-3,-2)M’(3,1)P’(4,3)思考: 1、在平面直角坐标系中,点(x,y)关于直线x=1对称点的坐标是多少? 2、在平面直角坐标系中,点(x, y)关于直线x=-1对称点的坐标是多少? 3、在平面直角坐标系中,点(x,y)关于直线y=1对称点的坐标是多少? (-x+2,y)(-x-2,y)(x,-y+2)关于与Y轴平行的直线的 对称点坐标的规律点(x,y)关于直线 x=m 对称的点的坐标是(2m-x,y).也就是说,若两点(a,b)、(c,d)关于直线x=m对称,则m=(a+c)/2,b=d.5.点M(a+b, -3)与点N (2,a)关于y=1轴对称,试求a、b的值。{a+b=2-3+a=0{a=3b=-24、在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是多少? (x,-y-2)拓 展 练 习1.如图 :在平面直角坐标系中A.B坐标分别为(2,0),(-1,3)。若△OAC与△OAB全等,试尽可能多的写出点C的坐标。3-121-103-31yxBAC3C2C1拓 展 练 习2. 已知两点A(0,2),B(4,1).点P是x轴上一点,使PA+PB的值最小,确定点P的位置3.点P的坐标为(a,b),它关于y轴的对称点为P1 ,而P1关于X轴的对称点为P2,点P2的坐标为(-3,1)。则a=--b=---------Oyx (-1,3) A
(-4,5) C(-4,1)B12345-1-4-3-2-5-1-212345A1(3,3)C1(6,5)B1(6,1)你能作出以A(-1,3)、B(-4,1)、C(-4,5)为三顶点的?ABC关于直线x=1对称的图形吗?关于与y轴平行的直线的一般规律是什么?6合作与讨论关于与Y轴平行的直线的 对称点坐标的规律点(x,y)关于直线 x=m 对称的点的坐标是(2m-x,y).也就是说,若两点(a,b)、(c,d)关于直线x=m对称,则m=(a+c)/2,b=d.关于与x轴平行的直线的对称点坐标的规律点(x,y)关于直线y=n对称点的坐标是(x,2n-y).
也就是说若两点(a,b)、(c,d)关于直线y=n对称,则a=c,n=(b+d)/2.我校要建A、B两个花坛,A花坛在水井O西面5米,再向北走3米,B花坛在水井O西面25米,再向北走6米,已知水井有通西方的水管,只能在水管上开一个出水口,则出水口应建在什么位置,请你告诉校长?怎么办中考练兵这是一个经过改装的台球桌面的示意图,图中四个角分别表示四个球袋,如一球在A处,沿图示方向经B处击出,可多次反射,试求球最后将落入的球袋坐标。AB1、学习了在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点。关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.课 堂 小 结
⑵点P(-3,2)关于y轴的对称点B的坐标。
⑶点P(-3,2)关于原点对称点P’的坐标。
⑷观察点A与B,点P与P’的位置关系是怎样的?点A与点B关于原点对称,点P与点P’关于原点对称·在你所画出的平面直角坐标系中,描出P’(3,-2)关于原点对称的两个点的坐标之间有什么关系?探索1小结:在平面直角坐标系中,关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.(x,-y)(-x,y)在平面直角坐标系中画出下列各点关于y轴的对称点.C ’ (-3, 4)··C(3, -4)·B’ (4, 2)·B(-4,-2)小结:在平面直角坐标系中,关于原点对称的点
横坐标互为相反数,
纵坐标互为相反数.点(x, y)关于x轴对称
的点的坐标为__ ____.(-x,-y)检验一下你的学习效果:
⒈点A(-1,3)关于原点对称的点的坐标是___________。
⒉点B(-3,0)关于原点对称的点的坐标是____________。
⒊点C(-x,y)关于原点对称的点的坐标是____________。
⒋若点A(m,-2),B(1,n)关于原点对称,则m=_____,n=_____。
⒌已知点P(x,y),xy>0,则点P关于原点的对称点在( )。
①第一象限 ②第三象限
③第一象限或第三象限 ④第二象限或第四象限
⒍已知点P(k,3),在直线y=x上,则点P关于原点对称的点的坐标是______________。
⒎下列各点中哪两个点关于原点对称?___________________。
A(-5,0), B(0,2), C(2,-1), D(2,0), E(0,5) F(-2,1) G(-2,-1)-12(1,-3)(3,0)(x,-y)③(-3,-3)点C(2,-1)与F(-2,1)1、完成下表.
(-2, 3)(2,-3)(-1,-2)(1, -2)(6, 5)(-6, 5)(0, 1.6)(0,1.6)(-4,0)(4,0)2、已知点P(2a+4,-3)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
若点p与点p’关于原点对称,则a=_____ b=_______.练 习1-6-52-613.下列图象中,一定关于原点对称的图象是( )
A.y=1/x B.y=2x+1 C.y=-2x+1 D.以上三种都有可能.如图,作出与△ABC关于原点对称的图形xyO-4 -3 -2 -1 1 2 3 4-12341-2-3A解:点A(-4,1) 、B(-3,2) 、C(-1,-1)关于原点对称的点的坐标分别是BC探索2A′B′C′则△A’B’C’就是 △ABC关于原点对称的图形
考考你的能力:
⑴在如图所示编号为①、②、③、④的四个三角形中,关于y轴对称的两个三角形的编号为 ;关于坐标原点O对称的两个三角形的编号为 。
⑵已知点Q(m,3)在双曲线y=-——上,则点Q关于原点对称
的点的坐标 。
⑶已知点A(a,3)和
点B(-4,b)关于原
点对称,则a=___,b=_____。
⑷已知点A关于原点对称点的坐标
为(a,b),那么点A关于y轴
对称点的坐标是 。
⑸已知点P(k,b)与点Q(2,
-4)关于原点对称,则直线y=
kx+b不经过 象限。
①与②①与③(a,-b)第三4-3xyO -5 -4 -3 -2 -1 1 2 3 4 5-12341-2-3 四边形ABCD各顶点的坐标分别为A(5,0),B(-2,3), C(-1,0), D(-1,-5),作出与四边形ABCD关于原点O对称的图形-4-55ABCD 平行四边形,A(1,2), B(-4,2), C(-2,-5),求出第四个点D的坐标.若平行四边形在坐标系内关于原点对称,已知点A,点B的坐标不变,点C,点D的坐标又是什么?拓 展 练 习1.如图 :在平面直角坐标系中A.B坐标分别为(2,0),(-1,3)。若△OAC与△OAB全等,试尽可能多的写出点C的坐标。3-121-103-31yxBAC3C2C12、(2008河南)如图,阴影部分组成的图案 既是关于x轴成轴对称的图形又是关于坐标原点O 成中心对称的图形.若点A的坐标是(1,3),则点M 和点N 的坐标分别是:M(-1,-3)N(1,-3)3、如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转90°得到直线A1B1.
(1)在图中画出直线A1B1.
(2)求出经过线段A1B1中点C的反比例函数解析式.
(3)是否存在另一条与直线AB平行的直线y=kx+b,它与双曲线只有一个交点,若存在,求此直线的函数解析式,若不存在,请说明理由.4.如图,在平面直角坐标系中, △ABC为等边三角形,其中点A,B,C的坐标分别为(-3,-1),(-3,-3),(-3+√3,-2),现以Y轴为对称轴作△ ABC的对称图形,得△ A1B1C1,再以X轴为对称轴作△ A1B1C1的对称图形,得△ A2B2C2.(1).直接写出C1,C2的坐标.(2).能否通过一次旋转将△ ABC旋转到△ A2B2C2的位置?你若认为能, 请出肯定的回答,你若认为不能请作出否定的回答(不必说明理由).(3).设当△ ABC的位置发生变化时, △ A2B2C2., △ A1B1C1与△ ABC之间的对称关系始终保持不变.
①当△ ABC向上平移多少个单位时, △ A1B1C1与△ A2B2C2完全重合?并直接写出此时C点的坐标.
②将△ ABC绕点A顺时针旋转多少度,使△ A1B1C1与△ A2B2C2重合,点C的坐标又是什么?
1、会求已知点关于原点对称的 点的坐标。
2、会利用坐标画出关于原点对称的图形。
探究3:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗?x=1······P(-2,3)M(-1,1)N’(5,-2)N(-3,-2)M’(3,1)P’(4,3)思考: 1、在平面直角坐标系中,点(x,y)关于直线x=1对称点的坐标是多少? 2、在平面直角坐标系中,点(x, y)关于直线x=-1对称点的坐标是多少? 3、在平面直角坐标系中,点(x,y)关于直线y=1对称点的坐标是多少? (-x+2,y)(-x-2,y)(x,-y+2)关于与Y轴平行的直线的 对称点坐标的规律点(x,y)关于直线 x=m 对称的点的坐标是(2m-x,y).也就是说,若两点(a,b)、(c,d)关于直线x=m对称,则m=(a+c)/2,b=d.5.点M(a+b, -3)与点N (2,a)关于y=1轴对称,试求a、b的值。{a+b=2-3+a=0{a=3b=-24、在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是多少? (x,-y-2)拓 展 练 习1.如图 :在平面直角坐标系中A.B坐标分别为(2,0),(-1,3)。若△OAC与△OAB全等,试尽可能多的写出点C的坐标。3-121-103-31yxBAC3C2C1拓 展 练 习2. 已知两点A(0,2),B(4,1).点P是x轴上一点,使PA+PB的值最小,确定点P的位置3.点P的坐标为(a,b),它关于y轴的对称点为P1 ,而P1关于X轴的对称点为P2,点P2的坐标为(-3,1)。则a=--b=---------Oyx (-1,3) A
(-4,5) C(-4,1)B12345-1-4-3-2-5-1-212345A1(3,3)C1(6,5)B1(6,1)你能作出以A(-1,3)、B(-4,1)、C(-4,5)为三顶点的?ABC关于直线x=1对称的图形吗?关于与y轴平行的直线的一般规律是什么?6合作与讨论关于与Y轴平行的直线的 对称点坐标的规律点(x,y)关于直线 x=m 对称的点的坐标是(2m-x,y).也就是说,若两点(a,b)、(c,d)关于直线x=m对称,则m=(a+c)/2,b=d.关于与x轴平行的直线的对称点坐标的规律点(x,y)关于直线y=n对称点的坐标是(x,2n-y).
也就是说若两点(a,b)、(c,d)关于直线y=n对称,则a=c,n=(b+d)/2.我校要建A、B两个花坛,A花坛在水井O西面5米,再向北走3米,B花坛在水井O西面25米,再向北走6米,已知水井有通西方的水管,只能在水管上开一个出水口,则出水口应建在什么位置,请你告诉校长?怎么办中考练兵这是一个经过改装的台球桌面的示意图,图中四个角分别表示四个球袋,如一球在A处,沿图示方向经B处击出,可多次反射,试求球最后将落入的球袋坐标。AB1、学习了在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点。关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.课 堂 小 结
同课章节目录
