5.3平行线的性质
图片预览




文档简介
课件20张PPT。5.3平行线的性质温故而知新个体预习生成1.看图回答:
(1)∠3=∠B,则EF∥AB,依据是
(2)∠2+∠A=180°,则DC∥AB,依据 是
(3)∠1=∠4,则GC∥EF,依据是
(4)GC ∥ EF,AB ∥ EF,则GC∥AB,依据是
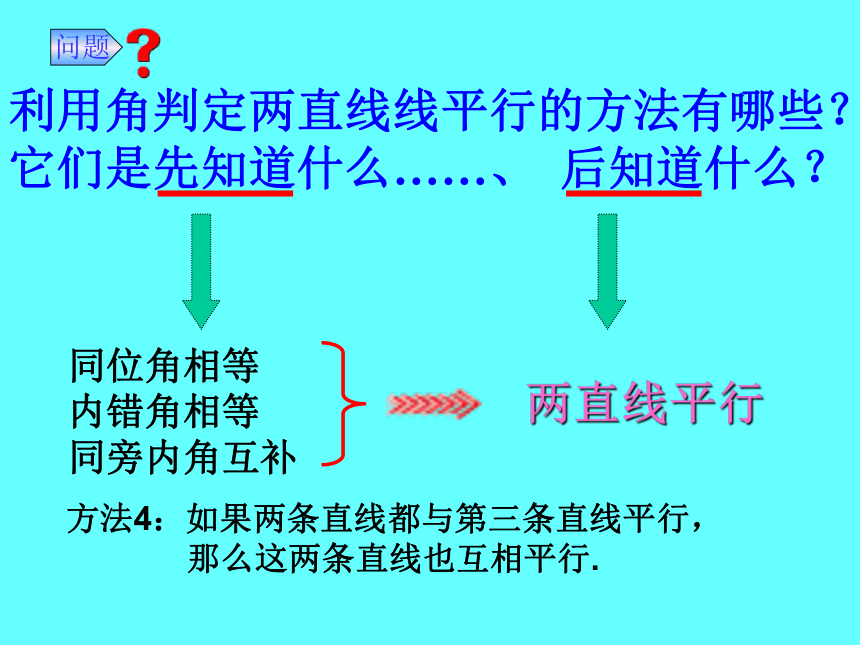
利用角判定两直线线平行的方法有哪些?
它们是先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行问题方法4:如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.温故而知新2.想一想:
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢?
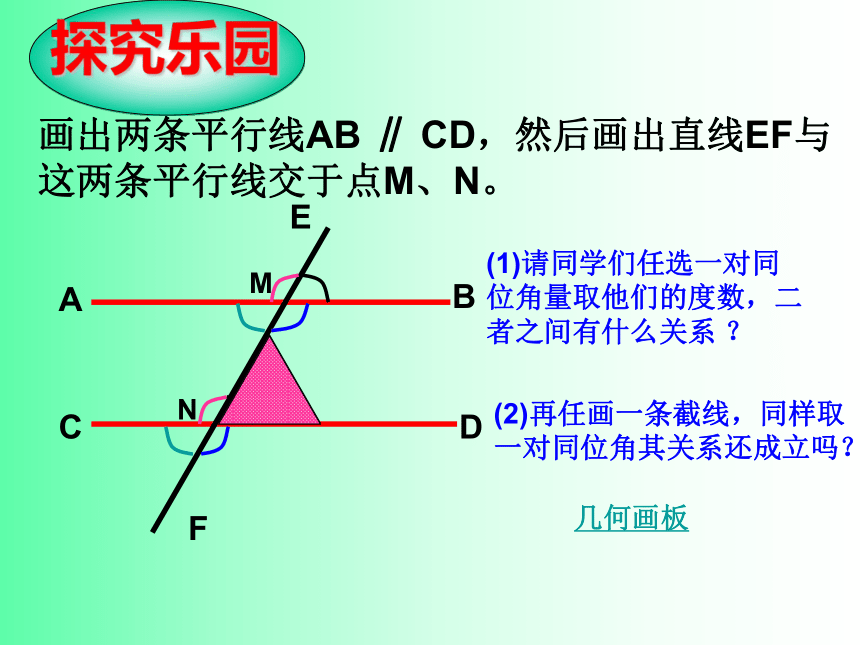
内错角,同旁内角之间又有什么关系呢?画出两条平行线AB ∥ CD,然后画出直线EF与
这两条平行线交于点M、N。(1)请同学们任选一对同位角量取他们的度数,二者之间有什么关系 ? (2)再任画一条截线,同样取
一对同位角其关系还成立吗?几何画板走组互助1、你能猜想出其他结论吗?2、你能根据性质1说出结论1
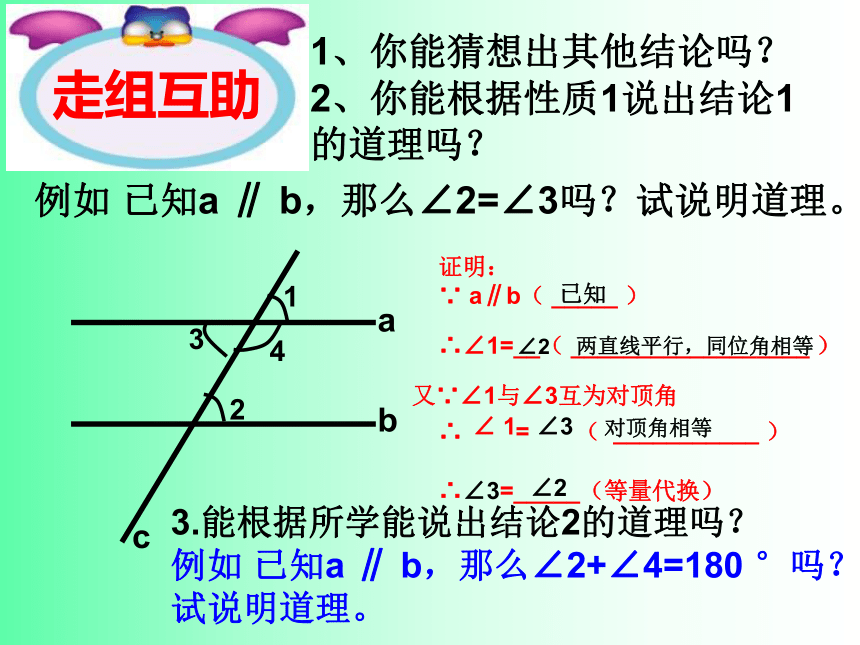
的道理吗?例如 已知a ∥ b,那么∠2=∠3吗?试说明道理。acb2143两直线平行,同位角相等∠2已知对顶角相等∠ 1 ∠3 3.能根据所学能说出结论2的道理吗?
例如 已知a ∥ b,那么∠2+∠4=180 °吗?
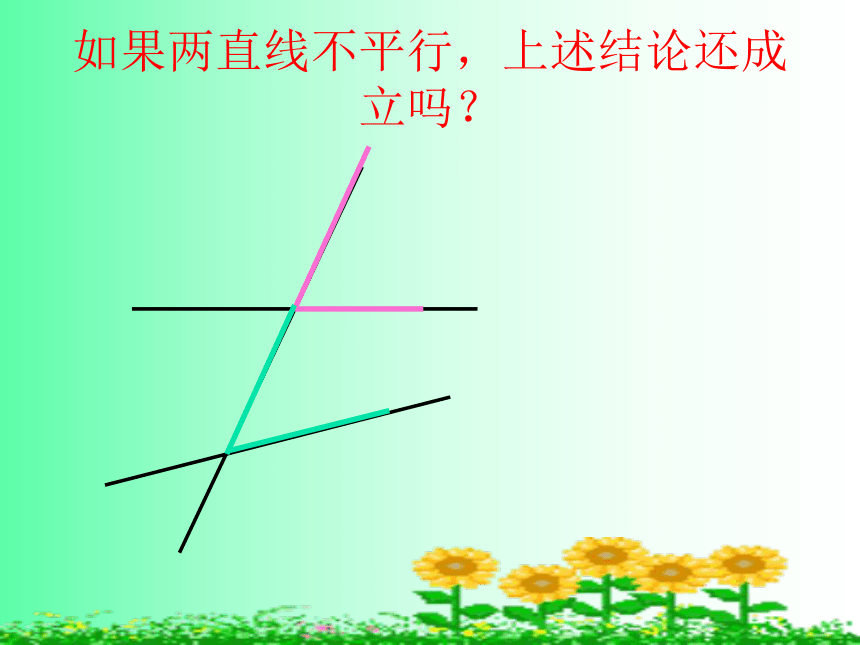
试说明道理。∠2如果两直线不平行,上述结论还成立吗?整理归纳: 平行线的性质:
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线 平行,同旁内角互补) 类比直线平行的
判定平行线的
性质由角的大小关系转化为直线的位置关系由直线的位置关系转化为角的大小关系1.如图 直线a∥b,∠1=54°,那么
∠2 、∠3、∠4各是多少度?为什么?3421展示质疑abcb341(2).从∠1=110°可以知道
∠4是多少度?为什么?(3).从∠1=110°可以知道
∠2是多少度?为什么?敏而好学展示质疑如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115° ,∠D=100 ° ,请你求出另外两个角的度数。学而时习之智慧闯关<冲击第一关>已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证:(1)DE∥BC
(2) ∠C的度数如图 AB ∥ CD ∥ EF, ∠ BAC+ ∠ ACE+ ∠ CEF=( )A.180 °D.540 °C.360 °B.270 °CABEDF<挑战第二关>如图 AB ∥ DE, ∠ 1 =∠ 2,
问AE与DC的位置关系?说明理由。21DCEBA∴ ∠ AED = ∠ 2证明:
∵AB ∥ DE(已知)(两直线平行,内错角相等)又∵ ∠1 = ∠ 2 (已知)∴ ∠ AED = ∠ 1(等量代换)<勇闯第三关>如图:已知 ?1= ? 2
求证:? BCD+ ? D=180?BC内错角相等,两直线平行两直线平行,同旁内角互补BC证明:如图
∵ ?1= ? 2(已知)
∴AD∥_____( )
∵AD ∥_____(已证)
∴ ? BCD+ ? D=180( )<闯关无极限> 如图,若AB//CD,你能确定∠B、∠D
与∠BED的大小关系吗?说说你的看法. 解答:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB. ……F<勇攀高峰>收获乐园学而不思则罔1.谈谈本节课你的收获与惑?
2.你想进一步探究的问题是什么?数学日记学而不厌作业阳光套餐金色套餐:
习题5.3 3,4,12.银色套餐:
习题5.3 2,3,4.绿色套餐:
习题5.3 2,3.诲人不倦悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考, 去发现,去总结。教师寄语再见
(1)∠3=∠B,则EF∥AB,依据是
(2)∠2+∠A=180°,则DC∥AB,依据 是
(3)∠1=∠4,则GC∥EF,依据是
(4)GC ∥ EF,AB ∥ EF,则GC∥AB,依据是
利用角判定两直线线平行的方法有哪些?
它们是先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行问题方法4:如果两条直线都与第三条直线平行, 那么这两条直线也互相平行.温故而知新2.想一想:
根据同位角相等可以判定两直线平行,反过来如果两直线平行同位角之间有什么关系呢?
内错角,同旁内角之间又有什么关系呢?画出两条平行线AB ∥ CD,然后画出直线EF与
这两条平行线交于点M、N。(1)请同学们任选一对同位角量取他们的度数,二者之间有什么关系 ? (2)再任画一条截线,同样取
一对同位角其关系还成立吗?几何画板走组互助1、你能猜想出其他结论吗?2、你能根据性质1说出结论1
的道理吗?例如 已知a ∥ b,那么∠2=∠3吗?试说明道理。acb2143两直线平行,同位角相等∠2已知对顶角相等∠ 1 ∠3 3.能根据所学能说出结论2的道理吗?
例如 已知a ∥ b,那么∠2+∠4=180 °吗?
试说明道理。∠2如果两直线不平行,上述结论还成立吗?整理归纳: 平行线的性质:
性质1:两直线平行,同位角相等.
∵ a∥b ( 已知 )
∴ ∠1=∠2(两直线平行,同位角相等)
性质2:两直线平行,内错角相等.
∵a∥b( 已知 )
∴ ∠1=∠3(两直线平行,内错角相等)
性质3:两直线平行,同旁内角互补.
∵a∥b( 已知 )
∴ ∠1+∠4=180° (两直线 平行,同旁内角互补) 类比直线平行的
判定平行线的
性质由角的大小关系转化为直线的位置关系由直线的位置关系转化为角的大小关系1.如图 直线a∥b,∠1=54°,那么
∠2 、∠3、∠4各是多少度?为什么?3421展示质疑abcb341(2).从∠1=110°可以知道
∠4是多少度?为什么?(3).从∠1=110°可以知道
∠2是多少度?为什么?敏而好学展示质疑如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115° ,∠D=100 ° ,请你求出另外两个角的度数。学而时习之智慧闯关<冲击第一关>已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
求证:(1)DE∥BC
(2) ∠C的度数如图 AB ∥ CD ∥ EF, ∠ BAC+ ∠ ACE+ ∠ CEF=( )A.180 °D.540 °C.360 °B.270 °CABEDF<挑战第二关>如图 AB ∥ DE, ∠ 1 =∠ 2,
问AE与DC的位置关系?说明理由。21DCEBA∴ ∠ AED = ∠ 2证明:
∵AB ∥ DE(已知)(两直线平行,内错角相等)又∵ ∠1 = ∠ 2 (已知)∴ ∠ AED = ∠ 1(等量代换)<勇闯第三关>如图:已知 ?1= ? 2
求证:? BCD+ ? D=180?BC内错角相等,两直线平行两直线平行,同旁内角互补BC证明:如图
∵ ?1= ? 2(已知)
∴AD∥_____( )
∵AD ∥_____(已证)
∴ ? BCD+ ? D=180( )<闯关无极限> 如图,若AB//CD,你能确定∠B、∠D
与∠BED的大小关系吗?说说你的看法. 解答:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴EF//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF
=∠DEB.
即∠B+∠D=∠DEB. ……F<勇攀高峰>收获乐园学而不思则罔1.谈谈本节课你的收获与惑?
2.你想进一步探究的问题是什么?数学日记学而不厌作业阳光套餐金色套餐:
习题5.3 3,4,12.银色套餐:
习题5.3 2,3,4.绿色套餐:
习题5.3 2,3.诲人不倦悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考, 去发现,去总结。教师寄语再见
