空间几何体的表面积与体积(教学案)
文档属性
| 名称 | 空间几何体的表面积与体积(教学案) |
|
|
| 格式 | rar | ||
| 文件大小 | 260.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-18 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
空间几何体的表面积与体积
1.3.1 柱体.锥体.台体的表面积与体积(一)
一.温故探新
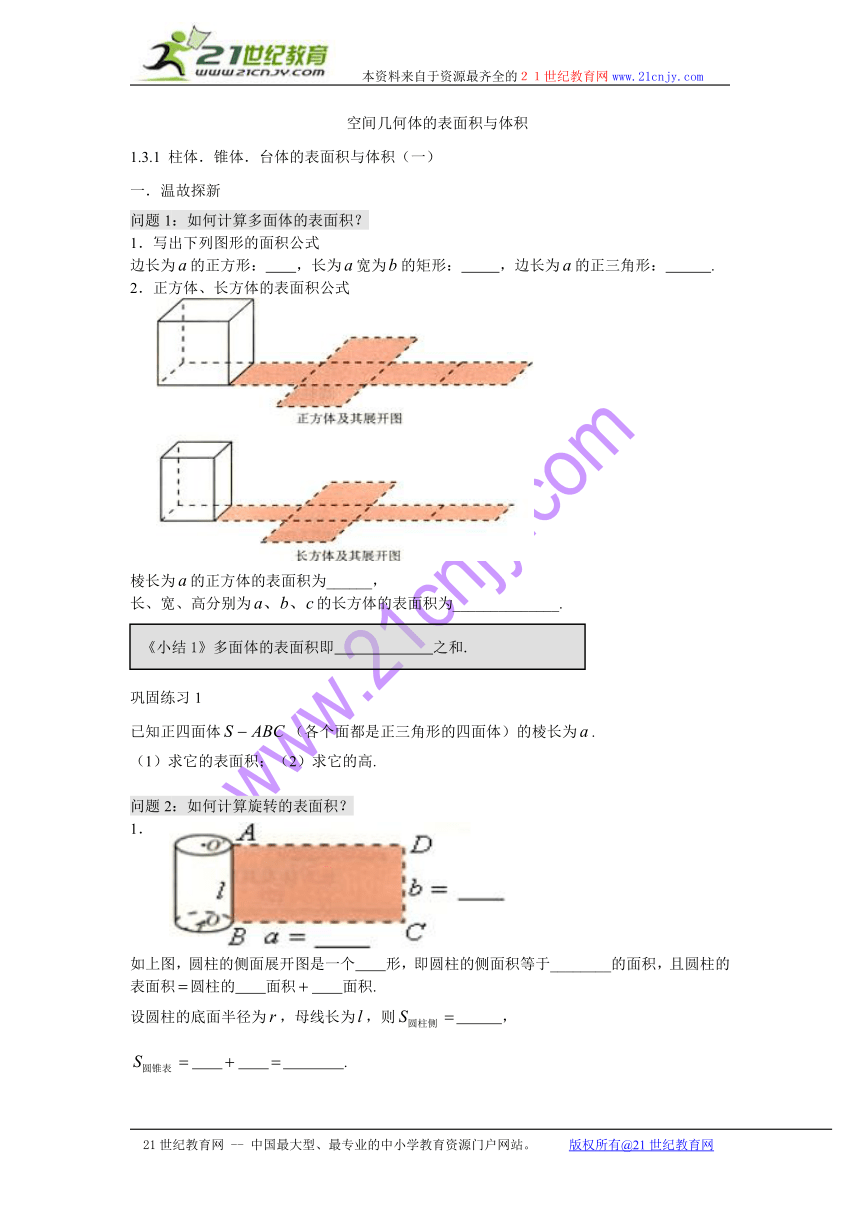
问题1:如何计算多面体的表面积?
1.写出下列图形的面积公式
边长为的正方形: ,长为宽为的矩形: ,边长为的正三角形: .
2.正方体、长方体的表面积公式
棱长为的正方体的表面积为______,
长、宽、高分别为的长方体的表面积为______________.
巩固练习1
已知正四面体(各个面都是正三角形的四面体)的棱长为.
(1)求它的表面积;(2)求它的高.
问题2:如何计算旋转的表面积?
1.
如上图,圆柱的侧面展开图是一个 形,即圆柱的侧面积等于________的面积,且圆柱的表面积圆柱的 面积 面积.
设圆柱的底面半径为,母线长为,则 ,
.
2.如右图,圆锥的侧面积展开图是 形,即圆锥的侧面积等于________的面积,且圆锥的表面积圆锥的 面积 面积.
设圆锥的底面半径为,母线长为,
则(熟记,以后证明),
.
3.如右图,圆台的侧面展开图示 形.
设圆台的上底半径为,下底半径为,母线长为,
则(熟记,以后证明)
.
巩固练习2
如图,一个圆台形花盆盆口直径为,盆底直径为底部渗水圆孔直径为盆壁长,为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆?(取3.14,结果精确到1毫升,可用计算器)
二.理解应用
题组3:
1.若圆台的上下底面半径分别为1和3,它们侧面积是两底面面积的
2倍,则圆台的切线场是( )
2.如果某个圆柱的底面面积为侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
题组4:如果某个圆锥的轴截面是正三角形,那么它的侧面积是底面积的_____倍.
三.拓展提高
一个圆锥的底面半径为,高为,在其中有一个高为的内接圆,求:
(1)试用表示圆柱的侧面积;
(2)当为何值时,圆柱的侧面积最大?
四.课外作业
1.若圆柱的侧面展开图示一个正方形,则这个圆柱的全面积与侧面积之比是( )
2.如果圆台的上底面半径为5,下底面半径为,中截面把圆台分为上.下两个圆台,它们的侧面积之比为1:2,那么 ( )
3.若圆锥的侧面展开图是原圆心角为,半径为的扇形,则这个圆锥的全面积与侧面积之比是( )
*4.某个圆台的母线长,母线与轴的夹角为,上底半径为,求圆台的高和侧面积.
*5.某个圆锥的高和底面半径相等,它的一个内接圆柱的高和圆柱底面的半径也相等,求圆柱的表面积和圆锥的表面积之比.
§1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积(二)
一.温故探新
问题1:还记得圆柱、圆锥、圆台和圆柱的侧面积公式吗?
, ,
巩固练习1
1.若圆柱的侧面展开图是一个边长为和的矩形,则这个圆柱的全面积为( )
2.已知圆锥的轴截面是等腰直角三角形,其侧面积,那么它的高等于______.
问题2:柱体、锥体、台体的体积公式是否也有与圆柱、圆锥、圆台的侧面积公式相类似的关系?
已知,若 ,则 ,
若 ,则 .
巩固练习2
1、 将边长为的正方形卷成一个圆柱的侧面,那么所成的圆柱的体
积为( )
2、 一个正方形和一个圆柱等高,且侧面积相等,则正方形和圆柱的
体积比为________.
二.理解应用
题组3:有一堆规格相同的铁制(铁的密度是)六角螺帽共重,已知底面是正六边形,边长为,内孔直径,问这堆螺帽大约有多少个(,可用计算器)
题组4
若正三棱台的两底面边长分别为2、8,侧棱长等于6,计算三棱台的体积.
三.拓展提高
下图是一个几何体的三视图(单位:),画出它的直观图,并求出她的表面积和体积.
四.课外作业
1.若干毫升水倒入底面半径为的圆柱形器皿中,量得水面高度为,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是( )
2.如右图,将一个长方体沿相邻的三个面的对角线
截出一个棱锥,则棱锥的体积与剩下的几何体体积
的比为________.
3.如图,一个三棱柱容器中盛有水,且
侧棱.若侧面水平放置
时,液面恰好过
的中点,当底面水平放置时,
液面高为_______.
*4.设正方体的棱长为1,求三棱锥的高.
*5.求底面边长为,侧棱长为的正三棱锥的表面积与体积.
§1.3 空间几何体的表面积与体积
1.3.2 球的体积和表面积
一.温故探新
问题1:球的表面积与体积公式有什么关系?
1.半径为的圆的周长 ,面积 .
2.半径为的球的表面积,体积
巩固练习1
1.若某球的体积与其表面积的数值相等,则此球的半径为______.
2.如果一个球的表面积比原来的扩大3倍,那么此球的体积比原来的扩大______倍.
问题2:长方体与它的外接球之间有什么关系
1.长方体的一个顶点的三条棱的长分别是3、4、5,且它的八个顶点都在同一个球面上,求这个球的表面积和体积.
巩固练习2
1.正方体的全面积是,它的顶点都在一个球面上,则此球的表面积是 ,体积是 .
2.长方体共顶点的三个侧面面积分别为,求它的外接球的表面积.
二.理解应用
题组3:
1.一个球的外切正方体的全面积等于6,则此球的体积为______.
2.如果球的表面积为,那么它的内接正方体与外切正方体的边长比为________.
题组4:
在球面上有四个点,若两两互相垂直,且,求这个球的表面积和体积.
三.拓展提高
一个四面体的所有棱长都为,四个顶点都在同一个球面上,求此球的表面积.
四.课外作业
1.已知某个球的外切圆台上、下底面半径分别为,那么这个球的半径为 .
2.圆柱体容器的内壁底面半径为5,两个直径是5的玻璃小球浸没于容器的水中若同时取出两个球,则容器中的水面将下降( )
3.在球心同侧有相距的来那个平行截面,他们的面积分别为和,求这个球的表面积.
*4.一个半球体内有一个内接圆柱,圆柱的一个底面在半球的球面上,另一个底面在球面上,球的半径为,求圆柱的侧面积的最大值.
*5.半球内有一个内接正方体,求这个半球的全面积与正方体的全面积之比.
《小结1》多面体的表面积即 之和.
《小结2》圆柱.圆锥.圆台的侧面积公式
______,______,_________.
《小结3》空间几何体的表面积几何体的____面积____面积.
《小结4》利用轴截面把 问题转化为 问题来解决
《课堂小结》圆柱、圆锥、圆台的侧面积公式之间的关系
《小结1》圆柱、圆锥、圆台的侧面积公式之间的关系
《小结2》柱体、锥体、台体的体积公式之间的关系
09
《小结3》求组合体的表面积和体积时 ,要注意组合体的结构特征,避免重叠和交叉.
《小结4》正棱台的高是 .
《课堂小结》圆柱、圆锥、圆台的侧面积公式之间的关系
柱体.锥体.台体的体积公式之间的关系
《小结1》球的表面积、体积公式只与球的 有关,
是以 为自变量的函数.
《小结2》长方体外接球的直径恰好是长方体的 .
《小结3》正方体既有 球,也有 球.
《小结4》三条线段两两互相垂直的问题可以通过构造_________来解决.
《课堂小结》
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
空间几何体的表面积与体积
1.3.1 柱体.锥体.台体的表面积与体积(一)
一.温故探新
问题1:如何计算多面体的表面积?
1.写出下列图形的面积公式
边长为的正方形: ,长为宽为的矩形: ,边长为的正三角形: .
2.正方体、长方体的表面积公式
棱长为的正方体的表面积为______,
长、宽、高分别为的长方体的表面积为______________.
巩固练习1
已知正四面体(各个面都是正三角形的四面体)的棱长为.
(1)求它的表面积;(2)求它的高.
问题2:如何计算旋转的表面积?
1.
如上图,圆柱的侧面展开图是一个 形,即圆柱的侧面积等于________的面积,且圆柱的表面积圆柱的 面积 面积.
设圆柱的底面半径为,母线长为,则 ,
.
2.如右图,圆锥的侧面积展开图是 形,即圆锥的侧面积等于________的面积,且圆锥的表面积圆锥的 面积 面积.
设圆锥的底面半径为,母线长为,
则(熟记,以后证明),
.
3.如右图,圆台的侧面展开图示 形.
设圆台的上底半径为,下底半径为,母线长为,
则(熟记,以后证明)
.
巩固练习2
如图,一个圆台形花盆盆口直径为,盆底直径为底部渗水圆孔直径为盆壁长,为了美化花盆的外观,需要涂油漆.已知每平方米用100毫升油漆,涂100个这样的花盆需要多少油漆?(取3.14,结果精确到1毫升,可用计算器)
二.理解应用
题组3:
1.若圆台的上下底面半径分别为1和3,它们侧面积是两底面面积的
2倍,则圆台的切线场是( )
2.如果某个圆柱的底面面积为侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
题组4:如果某个圆锥的轴截面是正三角形,那么它的侧面积是底面积的_____倍.
三.拓展提高
一个圆锥的底面半径为,高为,在其中有一个高为的内接圆,求:
(1)试用表示圆柱的侧面积;
(2)当为何值时,圆柱的侧面积最大?
四.课外作业
1.若圆柱的侧面展开图示一个正方形,则这个圆柱的全面积与侧面积之比是( )
2.如果圆台的上底面半径为5,下底面半径为,中截面把圆台分为上.下两个圆台,它们的侧面积之比为1:2,那么 ( )
3.若圆锥的侧面展开图是原圆心角为,半径为的扇形,则这个圆锥的全面积与侧面积之比是( )
*4.某个圆台的母线长,母线与轴的夹角为,上底半径为,求圆台的高和侧面积.
*5.某个圆锥的高和底面半径相等,它的一个内接圆柱的高和圆柱底面的半径也相等,求圆柱的表面积和圆锥的表面积之比.
§1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积与体积(二)
一.温故探新
问题1:还记得圆柱、圆锥、圆台和圆柱的侧面积公式吗?
, ,
巩固练习1
1.若圆柱的侧面展开图是一个边长为和的矩形,则这个圆柱的全面积为( )
2.已知圆锥的轴截面是等腰直角三角形,其侧面积,那么它的高等于______.
问题2:柱体、锥体、台体的体积公式是否也有与圆柱、圆锥、圆台的侧面积公式相类似的关系?
已知,若 ,则 ,
若 ,则 .
巩固练习2
1、 将边长为的正方形卷成一个圆柱的侧面,那么所成的圆柱的体
积为( )
2、 一个正方形和一个圆柱等高,且侧面积相等,则正方形和圆柱的
体积比为________.
二.理解应用
题组3:有一堆规格相同的铁制(铁的密度是)六角螺帽共重,已知底面是正六边形,边长为,内孔直径,问这堆螺帽大约有多少个(,可用计算器)
题组4
若正三棱台的两底面边长分别为2、8,侧棱长等于6,计算三棱台的体积.
三.拓展提高
下图是一个几何体的三视图(单位:),画出它的直观图,并求出她的表面积和体积.
四.课外作业
1.若干毫升水倒入底面半径为的圆柱形器皿中,量得水面高度为,若将这些水倒入轴截面是正三角形的倒圆锥形器皿中,则水面的高度是( )
2.如右图,将一个长方体沿相邻的三个面的对角线
截出一个棱锥,则棱锥的体积与剩下的几何体体积
的比为________.
3.如图,一个三棱柱容器中盛有水,且
侧棱.若侧面水平放置
时,液面恰好过
的中点,当底面水平放置时,
液面高为_______.
*4.设正方体的棱长为1,求三棱锥的高.
*5.求底面边长为,侧棱长为的正三棱锥的表面积与体积.
§1.3 空间几何体的表面积与体积
1.3.2 球的体积和表面积
一.温故探新
问题1:球的表面积与体积公式有什么关系?
1.半径为的圆的周长 ,面积 .
2.半径为的球的表面积,体积
巩固练习1
1.若某球的体积与其表面积的数值相等,则此球的半径为______.
2.如果一个球的表面积比原来的扩大3倍,那么此球的体积比原来的扩大______倍.
问题2:长方体与它的外接球之间有什么关系
1.长方体的一个顶点的三条棱的长分别是3、4、5,且它的八个顶点都在同一个球面上,求这个球的表面积和体积.
巩固练习2
1.正方体的全面积是,它的顶点都在一个球面上,则此球的表面积是 ,体积是 .
2.长方体共顶点的三个侧面面积分别为,求它的外接球的表面积.
二.理解应用
题组3:
1.一个球的外切正方体的全面积等于6,则此球的体积为______.
2.如果球的表面积为,那么它的内接正方体与外切正方体的边长比为________.
题组4:
在球面上有四个点,若两两互相垂直,且,求这个球的表面积和体积.
三.拓展提高
一个四面体的所有棱长都为,四个顶点都在同一个球面上,求此球的表面积.
四.课外作业
1.已知某个球的外切圆台上、下底面半径分别为,那么这个球的半径为 .
2.圆柱体容器的内壁底面半径为5,两个直径是5的玻璃小球浸没于容器的水中若同时取出两个球,则容器中的水面将下降( )
3.在球心同侧有相距的来那个平行截面,他们的面积分别为和,求这个球的表面积.
*4.一个半球体内有一个内接圆柱,圆柱的一个底面在半球的球面上,另一个底面在球面上,球的半径为,求圆柱的侧面积的最大值.
*5.半球内有一个内接正方体,求这个半球的全面积与正方体的全面积之比.
《小结1》多面体的表面积即 之和.
《小结2》圆柱.圆锥.圆台的侧面积公式
______,______,_________.
《小结3》空间几何体的表面积几何体的____面积____面积.
《小结4》利用轴截面把 问题转化为 问题来解决
《课堂小结》圆柱、圆锥、圆台的侧面积公式之间的关系
《小结1》圆柱、圆锥、圆台的侧面积公式之间的关系
《小结2》柱体、锥体、台体的体积公式之间的关系
09
《小结3》求组合体的表面积和体积时 ,要注意组合体的结构特征,避免重叠和交叉.
《小结4》正棱台的高是 .
《课堂小结》圆柱、圆锥、圆台的侧面积公式之间的关系
柱体.锥体.台体的体积公式之间的关系
《小结1》球的表面积、体积公式只与球的 有关,
是以 为自变量的函数.
《小结2》长方体外接球的直径恰好是长方体的 .
《小结3》正方体既有 球,也有 球.
《小结4》三条线段两两互相垂直的问题可以通过构造_________来解决.
《课堂小结》
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
