空间与图形领域的考点分析与复习策略
图片预览





文档简介
课件77张PPT。2011中考数学 空间与图形领域
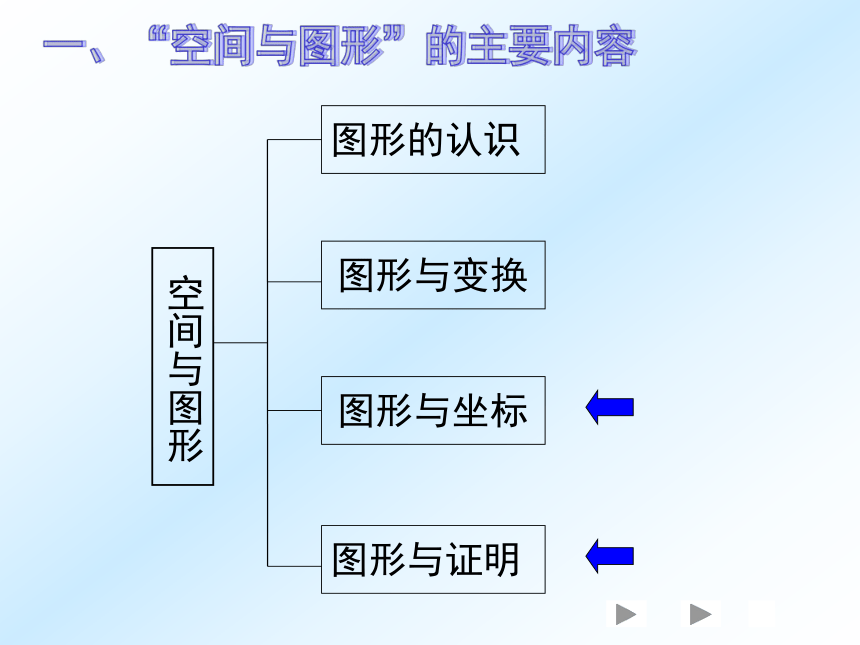
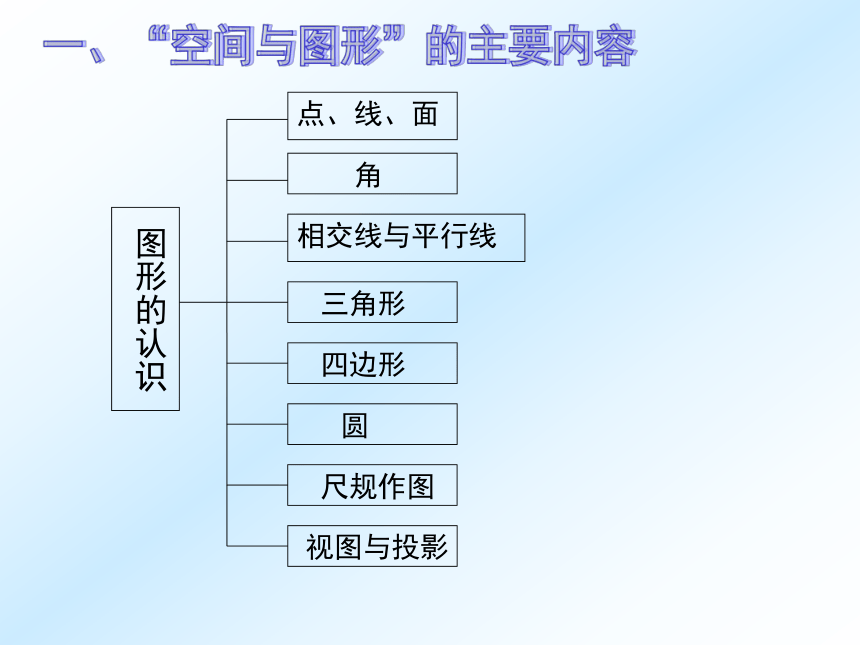
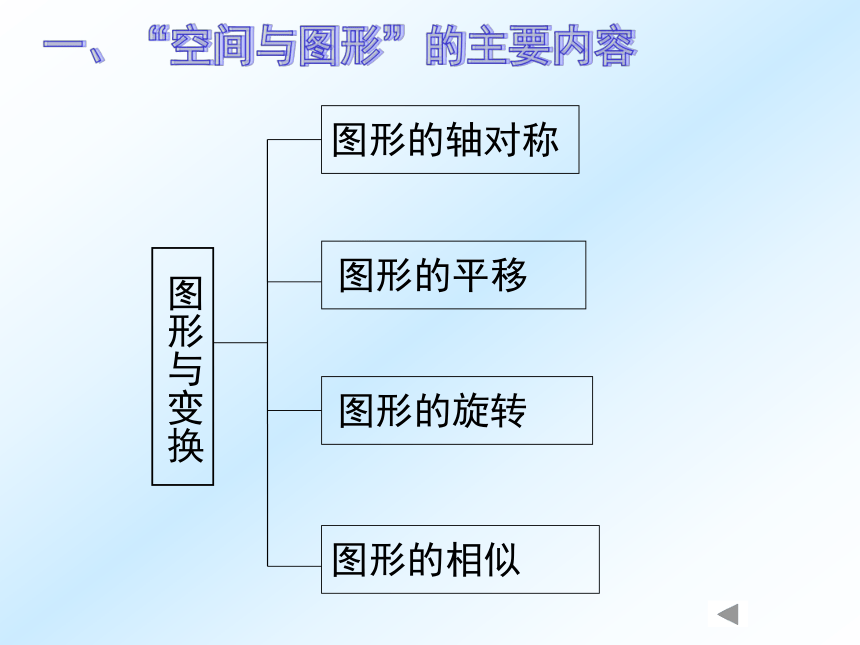
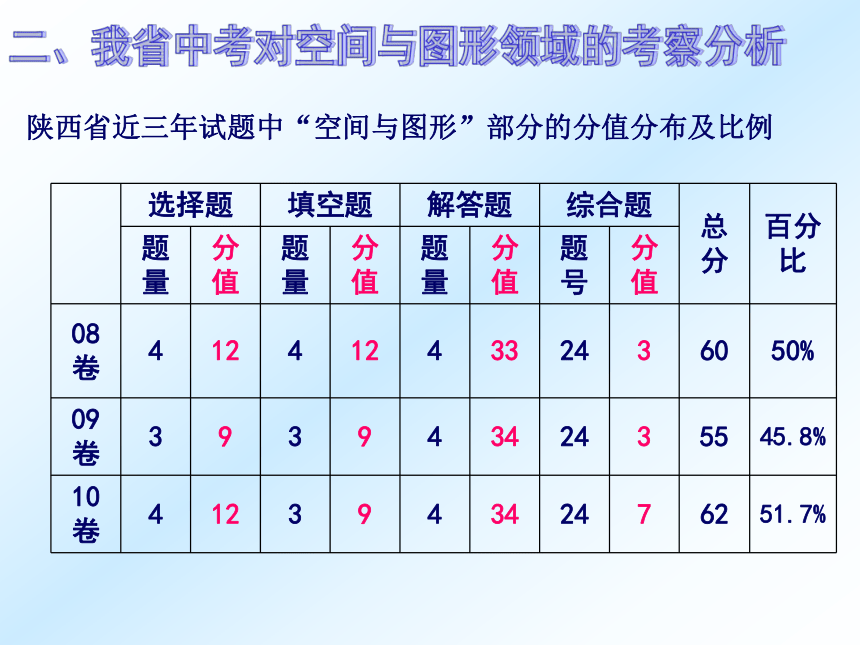
的考点分析与复习策略西安爱知中学 谷欣宇 Ⅰ 空间与图形领域的考点分析Ⅱ 空间与图形领域的复习策略提纲:一、“空间与图形”的主要内容一、“空间与图形”的主要内容一、“空间与图形”的主要内容陕西省近三年试题中“空间与图形”部分的分值分布及比例二、我省中考对空间与图形领域的考察分析三、考点分析:(-)相交线与平行线1、余角、补角、对顶角的概念和性质2、垂线、垂线段的概念,垂线段最短的性质3、平行线的性质和判定 “相交线与平行线”主要借助角来研究平面内两
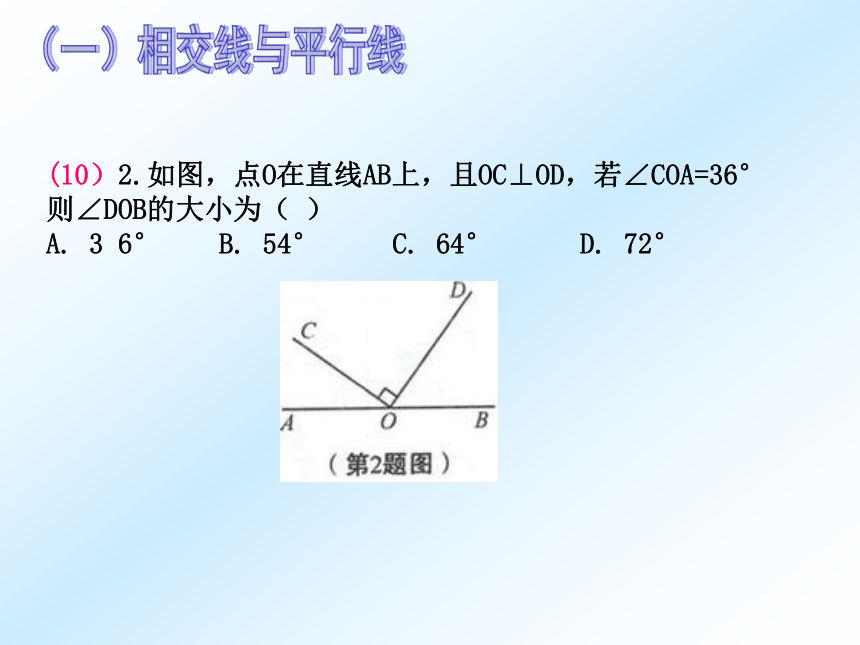
条直线之间位置关系.“两条直线的位置关系与相关角之间关系的转换,或角度的计算”是这一部分的基础性内容.(10)2.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°则∠DOB的大小为( )
A. 3 6° B. 54° C. 64° D. 72° (一)相交线与平行线(一)相交线与平行线1、同一个三角形中各个元素之间的关系(边之间的关系、角之间的关系、边与角之间的关系),以及有关的重要线段(高线、中线、角平分线、中位线)2、两个三角形之间的全等关系(性质与判定)
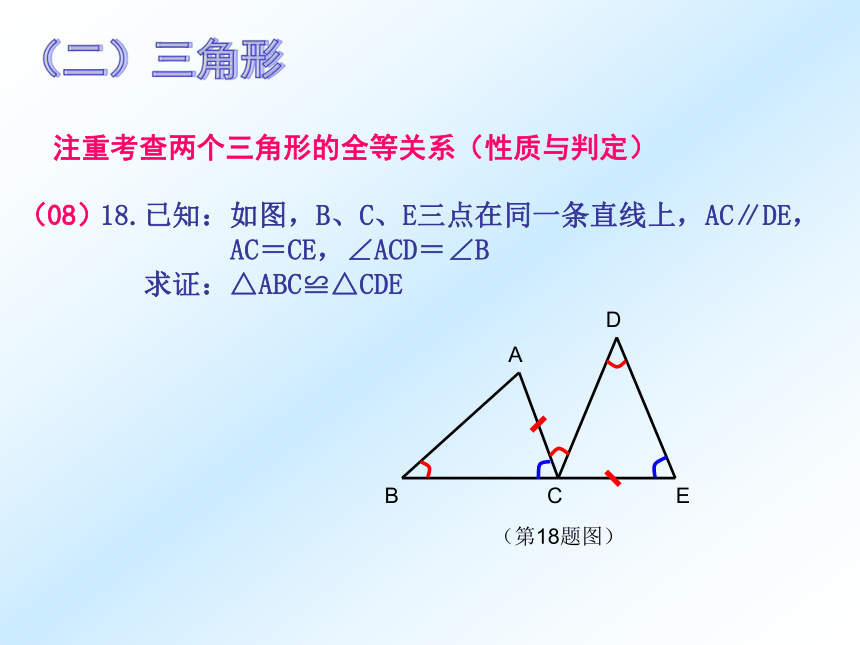
三、考点分析:(二)三角形(二)三角形(二)三角形注重考查两个三角形的全等关系(性质与判定)(二)三角形注重考查两个三角形的全等关系(性质与判定)注重考查两个三角形的全等关系(性质与判定)(10)18.如图,A、B、C三点在同一条直线上,AB=2BC.分别以AB、BC为边做正方形ABEF和正方形BCMN连接FN,EC.
求证:FN=EC . (二)三角形三、考点分析:(三)四边形1、考查特殊四边形的性质和判定,注重灵活运
用2、考查探究与推理,注重联系与综合 四边形是平面几何研究的主要对象,四边形的知识是平行线和三角形知识的应用和深化.
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
(三)四边形E(三)四边形重视总结通性通法,提高解题能力EF(三)四边形(三)四边形(10)24.如图,在平面直角坐标系中,抛物线经过A(-1,0),B(3,0)C(0,-1)三点.
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(三)四边形(三)四边形3(三)四边形-11(10)25.问题探究
(1)请你在图①中做一条直线,使它将矩形ABCD分成面积相等的两部分;
(2)如图②,点M是矩形ABCD内一点.请你在图②中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分.
问题解决
(3)如图③,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,BC=4,CD=4.开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处。为了方便驻区单位,准备过点P修一条笔直的道路(路的宽度不计),并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分.你认为直线l是否存在?若存在求出直线l的表达式;若不存在,请说明理由.(三)四边形(1)做一条直线,使它将矩形ABCD分成面积相等的两部分(2)过点M作一条直线,使它将矩形ABCD分成面积相等的两部分.
P(3)在直角梯形OBCD中,DC∥OB,OB=6,BC=4,CD=4.过
点P(4,2)作一条直线l,使直线l将直角梯形OBCD
分成面积相等的两部分.AHF图形面积分割图形面积分割(3)在直角梯形OBCD中,DC∥OB,OB=6,BC=4,CD=4.过
点P(4,2)作一条直线l,使直线l将直角梯形OBCD
分成面积相等的两部分.NKGMH考点分析:(四)圆1、圆的有关概念和性质,弧、弦、圆心角、圆
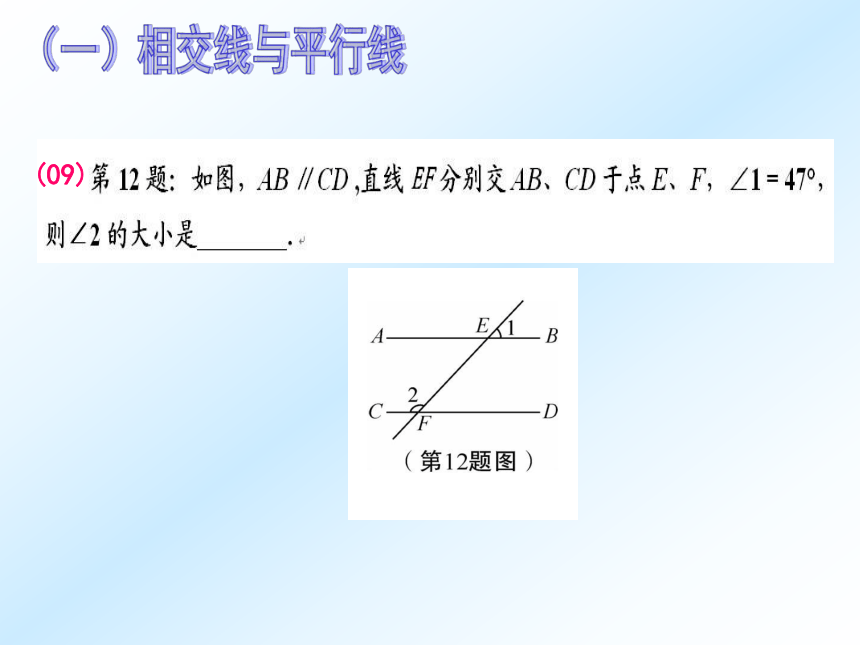
周角之间的关系;2、直线与圆以及圆与圆的位置关系3、与圆有关的计算(09)3.图中圆与圆之间不同的位置关系有( )
A.2种 B.3种 C.4种 D.5种(四)圆(四)圆(四)圆(10)9.如图,点A、B、P在⊙O上,且∠APB=50°,若点M是⊙O上的动点,要使△ABM为等腰三角形,则所有符合条件的点M有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
(四)圆(四)圆(10)23.如图,在Rt△ABC中,∠ABC=90°,斜边AC的垂直平分线交BC于点D,交AC于点E,连接BE.
(1)若BE是△DEC的外接圆的切线,求∠C的大小;
(2)当AB=1,BC=2时,求△DEC外接圆的半径.(四)圆(2)当AB=1,BC=2时,求△DEC外接圆的半径.
(四)圆12考点分析:(五)视图与投影1、考查几何体的“三视图”
(五)视图与投影1、考查“三视图”2、利用几何体的展开与折叠考查空间观念(五)视图与投影3、密切联系实际,加强对平行投影与中心投影的考查(五)视图与投影(五)视图与投影3、密切联系实际,加强对平行投影与中心投影的考查考点分析:(六)轴对称、平移与旋转这三种变换刻画了“两个全等图形”特定的位置关系2、利用轴对称性质解决最短路线问题;3、借助网格或坐标系,进行平移、旋转、轴对称
的作图;4、以旋转为前提,综合考查学生的探究能力1、图形折叠中的计算与证明;(08)23.某县社会主义新农村建设办公室,为了解决
该 县甲、乙两村和一所中学长期存在的饮水困难问
题,想在这三个地方的其中一处建一所供水站,由
供水站直接铺设管道到另外两处.
(六)轴对称、平移与旋转(六)轴对称、平移与旋转考点分析:(七)相似形1、突出“双基”,灵活考查三角形相似的判定与性质2、借助“应用”,灵活考查相似三角形的性质。(七)相似三角形:(1)应用相似三角形测物高、测距离(2)与圆相结合,求线段的长考点分析:(八)锐角三角函数 200100考点分析:(九)图形与坐标 “图形与坐标”是将图形放入平面直角坐标系里,以通过量化的方式来研究图形和图形之间的关系,体现了形与数的统一。它是许多几何图形问题与代数问题相结合的纽带和桥梁。(九)图形与坐标考点分析:(十)图形与证明 “证明”的表现和运用,不仅仅在要求证明的题目中,而是渗透和应用在几乎对所有的数学知识学习及运用的过程之中。掌握和运用证明是一个渐进、长期的过程,体现在诸多章节的学习之中。 1、单纯演绎推理的题目难度降低,位置前移,且数量大大减少
2、将合情推理与演绎推理有机融为一体加以考查3、操作、开放、探究性问题与证明结合,考查学生的综合能力。复习策略:一、研究标准和考试说明,分析中考试题,把握复习方向1.《数学课程标准》
2.《陕西省初中毕业学业考试说明》
3. 陕西省近5年的中考题复习策略:二、结合本校实际,制定合理的复习计划第一阶段:全面复习——夯实基础
第二阶段:专题复习——能力提升
第三阶段:模拟强化——查漏补缺
每个阶段要根据学生实际制定合理的教学目标第一阶段——全面复习1、构建知识网络,加强知识之间的内在联系 中考复习要把三年螺旋上升的知识分
成块,整理成知识网络,使学生对所学知
识有一个整体把握,有利于学生对知识的
理解和记忆2、重视数学双基训练第一阶段——全面复习3、重视总结通性通法,提高解题能力重视总结通性通法,提高解题能力重视总结通性通法,提高解题能力记住一些常用数据、常用图形可以提高解题速度重视总结通性通法,提高解题能力重视总结通性通法,提高解题能力记住一些常用数据、常用图形可以提高解题速度最短路线问题ABA′C重视总结通性通法,提高解题能力最短路线问题(08四川广安)如图,在菱形ABCD中,∠BAD=60o ,M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是3,则AB长为 .P′最短路线问题(09四川达州)如图6,在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为____________㎝.P′最短路线问题A′P′A. B.
C. 1 D. 2(08)25.最短路线问题 某县社会主义新农村建设办公室,为了解决该 县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处.
如图,甲、乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学?点B在点M的北偏西30°的3 km处,点A在点M的正西方向,点D在点M的南偏西60°的 23 km处.
为使供水站铺设到另两处的管道长度之和最短.现有如下三种方案:最短路线问题 方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
·最短路线问题 方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
M′最短路线问题 方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.
M′3、重视总结通性通法,提高解题能力最短路线问题第一阶段——全面复习B′M′N′N′N〃M′第一阶段——全面复习5、注重错题分析,定期让学生错题重做☆大多数学生掌握不好的难点内容
☆多数学生易犯的错误4、通过“一题多解”“多题归一”“一题多变”
的训练增强学生的思维能力.第二阶段——专题复习第一部分:数学思想与方法
专题一:分类讨论思想
专题二:转化思想
专题三:数学建模思想
第二部分:热点题型分类解析
专题四:阅读理解问题 专题五:动态图形研究
专题六:开放与探究 专题七:面积问题 任务和目标 本阶段的复习是对初中阶段重难点知识的深化和综合,是解题能力全面提升的阶段。主要任务是完成试卷中非单一知识点的考察,即中等以上难度的试题,要求学生有较高的文字解读能力,信息整合的方法,提炼建模的意识和较强的综合运用能力(探究与猜想、推理与计算)等。所以该阶段的复习应精讲精练,从培养关键点用数学的意识入手,达到事半功倍的效果。第二阶段——专题复习第三阶段——模拟强化 该阶段的主要任务是查漏补缺,调试身心,增强应试技巧和策略,从知识上弥补前期复习的疏漏,从心理上增强学生的自信心。所以模拟题的难度贴近中考试题,同时多一些创新和猜想,但仅限于极少数试题,不宜给学生造成心理恐慌。因此教师自身也应沉着自信,同时强调学生书写试卷的规范性,防止在不改错的地方失分。谢谢!
的考点分析与复习策略西安爱知中学 谷欣宇 Ⅰ 空间与图形领域的考点分析Ⅱ 空间与图形领域的复习策略提纲:一、“空间与图形”的主要内容一、“空间与图形”的主要内容一、“空间与图形”的主要内容陕西省近三年试题中“空间与图形”部分的分值分布及比例二、我省中考对空间与图形领域的考察分析三、考点分析:(-)相交线与平行线1、余角、补角、对顶角的概念和性质2、垂线、垂线段的概念,垂线段最短的性质3、平行线的性质和判定 “相交线与平行线”主要借助角来研究平面内两
条直线之间位置关系.“两条直线的位置关系与相关角之间关系的转换,或角度的计算”是这一部分的基础性内容.(10)2.如图,点O在直线AB上,且OC⊥OD,若∠COA=36°则∠DOB的大小为( )
A. 3 6° B. 54° C. 64° D. 72° (一)相交线与平行线(一)相交线与平行线1、同一个三角形中各个元素之间的关系(边之间的关系、角之间的关系、边与角之间的关系),以及有关的重要线段(高线、中线、角平分线、中位线)2、两个三角形之间的全等关系(性质与判定)
三、考点分析:(二)三角形(二)三角形(二)三角形注重考查两个三角形的全等关系(性质与判定)(二)三角形注重考查两个三角形的全等关系(性质与判定)注重考查两个三角形的全等关系(性质与判定)(10)18.如图,A、B、C三点在同一条直线上,AB=2BC.分别以AB、BC为边做正方形ABEF和正方形BCMN连接FN,EC.
求证:FN=EC . (二)三角形三、考点分析:(三)四边形1、考查特殊四边形的性质和判定,注重灵活运
用2、考查探究与推理,注重联系与综合 四边形是平面几何研究的主要对象,四边形的知识是平行线和三角形知识的应用和深化.
A.AB=CD B.AD=BC C.AB=BC D.AC=BD
(三)四边形E(三)四边形重视总结通性通法,提高解题能力EF(三)四边形(三)四边形(10)24.如图,在平面直角坐标系中,抛物线经过A(-1,0),B(3,0)C(0,-1)三点.
(1)求该抛物线的表达式;
(2)点Q在y轴上,点P在抛物线上,要使Q、P、A、B为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(三)四边形(三)四边形3(三)四边形-11(10)25.问题探究
(1)请你在图①中做一条直线,使它将矩形ABCD分成面积相等的两部分;
(2)如图②,点M是矩形ABCD内一点.请你在图②中过点M作一条直线,使它将矩形ABCD分成面积相等的两部分.
问题解决
(3)如图③,在平面直角坐标系中,直角梯形OBCD是某市将要筹建的高新技术开发区用地示意图,其中DC∥OB,OB=6,BC=4,CD=4.开发区综合服务管理委员会(其占地面积不计)设在点P(4,2)处。为了方便驻区单位,准备过点P修一条笔直的道路(路的宽度不计),并且使这条路所在的直线l将直角梯形OBCD分成面积相等的两部分.你认为直线l是否存在?若存在求出直线l的表达式;若不存在,请说明理由.(三)四边形(1)做一条直线,使它将矩形ABCD分成面积相等的两部分(2)过点M作一条直线,使它将矩形ABCD分成面积相等的两部分.
P(3)在直角梯形OBCD中,DC∥OB,OB=6,BC=4,CD=4.过
点P(4,2)作一条直线l,使直线l将直角梯形OBCD
分成面积相等的两部分.AHF图形面积分割图形面积分割(3)在直角梯形OBCD中,DC∥OB,OB=6,BC=4,CD=4.过
点P(4,2)作一条直线l,使直线l将直角梯形OBCD
分成面积相等的两部分.NKGMH考点分析:(四)圆1、圆的有关概念和性质,弧、弦、圆心角、圆
周角之间的关系;2、直线与圆以及圆与圆的位置关系3、与圆有关的计算(09)3.图中圆与圆之间不同的位置关系有( )
A.2种 B.3种 C.4种 D.5种(四)圆(四)圆(四)圆(10)9.如图,点A、B、P在⊙O上,且∠APB=50°,若点M是⊙O上的动点,要使△ABM为等腰三角形,则所有符合条件的点M有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
(四)圆(四)圆(10)23.如图,在Rt△ABC中,∠ABC=90°,斜边AC的垂直平分线交BC于点D,交AC于点E,连接BE.
(1)若BE是△DEC的外接圆的切线,求∠C的大小;
(2)当AB=1,BC=2时,求△DEC外接圆的半径.(四)圆(2)当AB=1,BC=2时,求△DEC外接圆的半径.
(四)圆12考点分析:(五)视图与投影1、考查几何体的“三视图”
(五)视图与投影1、考查“三视图”2、利用几何体的展开与折叠考查空间观念(五)视图与投影3、密切联系实际,加强对平行投影与中心投影的考查(五)视图与投影(五)视图与投影3、密切联系实际,加强对平行投影与中心投影的考查考点分析:(六)轴对称、平移与旋转这三种变换刻画了“两个全等图形”特定的位置关系2、利用轴对称性质解决最短路线问题;3、借助网格或坐标系,进行平移、旋转、轴对称
的作图;4、以旋转为前提,综合考查学生的探究能力1、图形折叠中的计算与证明;(08)23.某县社会主义新农村建设办公室,为了解决
该 县甲、乙两村和一所中学长期存在的饮水困难问
题,想在这三个地方的其中一处建一所供水站,由
供水站直接铺设管道到另外两处.
(六)轴对称、平移与旋转(六)轴对称、平移与旋转考点分析:(七)相似形1、突出“双基”,灵活考查三角形相似的判定与性质2、借助“应用”,灵活考查相似三角形的性质。(七)相似三角形:(1)应用相似三角形测物高、测距离(2)与圆相结合,求线段的长考点分析:(八)锐角三角函数 200100考点分析:(九)图形与坐标 “图形与坐标”是将图形放入平面直角坐标系里,以通过量化的方式来研究图形和图形之间的关系,体现了形与数的统一。它是许多几何图形问题与代数问题相结合的纽带和桥梁。(九)图形与坐标考点分析:(十)图形与证明 “证明”的表现和运用,不仅仅在要求证明的题目中,而是渗透和应用在几乎对所有的数学知识学习及运用的过程之中。掌握和运用证明是一个渐进、长期的过程,体现在诸多章节的学习之中。 1、单纯演绎推理的题目难度降低,位置前移,且数量大大减少
2、将合情推理与演绎推理有机融为一体加以考查3、操作、开放、探究性问题与证明结合,考查学生的综合能力。复习策略:一、研究标准和考试说明,分析中考试题,把握复习方向1.《数学课程标准》
2.《陕西省初中毕业学业考试说明》
3. 陕西省近5年的中考题复习策略:二、结合本校实际,制定合理的复习计划第一阶段:全面复习——夯实基础
第二阶段:专题复习——能力提升
第三阶段:模拟强化——查漏补缺
每个阶段要根据学生实际制定合理的教学目标第一阶段——全面复习1、构建知识网络,加强知识之间的内在联系 中考复习要把三年螺旋上升的知识分
成块,整理成知识网络,使学生对所学知
识有一个整体把握,有利于学生对知识的
理解和记忆2、重视数学双基训练第一阶段——全面复习3、重视总结通性通法,提高解题能力重视总结通性通法,提高解题能力重视总结通性通法,提高解题能力记住一些常用数据、常用图形可以提高解题速度重视总结通性通法,提高解题能力重视总结通性通法,提高解题能力记住一些常用数据、常用图形可以提高解题速度最短路线问题ABA′C重视总结通性通法,提高解题能力最短路线问题(08四川广安)如图,在菱形ABCD中,∠BAD=60o ,M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是3,则AB长为 .P′最短路线问题(09四川达州)如图6,在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为____________㎝.P′最短路线问题A′P′A. B.
C. 1 D. 2(08)25.最短路线问题 某县社会主义新农村建设办公室,为了解决该 县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处.
如图,甲、乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学?点B在点M的北偏西30°的3 km处,点A在点M的正西方向,点D在点M的南偏西60°的 23 km处.
为使供水站铺设到另两处的管道长度之和最短.现有如下三种方案:最短路线问题 方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
·最短路线问题 方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
M′最短路线问题 方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值.
M′3、重视总结通性通法,提高解题能力最短路线问题第一阶段——全面复习B′M′N′N′N〃M′第一阶段——全面复习5、注重错题分析,定期让学生错题重做☆大多数学生掌握不好的难点内容
☆多数学生易犯的错误4、通过“一题多解”“多题归一”“一题多变”
的训练增强学生的思维能力.第二阶段——专题复习第一部分:数学思想与方法
专题一:分类讨论思想
专题二:转化思想
专题三:数学建模思想
第二部分:热点题型分类解析
专题四:阅读理解问题 专题五:动态图形研究
专题六:开放与探究 专题七:面积问题 任务和目标 本阶段的复习是对初中阶段重难点知识的深化和综合,是解题能力全面提升的阶段。主要任务是完成试卷中非单一知识点的考察,即中等以上难度的试题,要求学生有较高的文字解读能力,信息整合的方法,提炼建模的意识和较强的综合运用能力(探究与猜想、推理与计算)等。所以该阶段的复习应精讲精练,从培养关键点用数学的意识入手,达到事半功倍的效果。第二阶段——专题复习第三阶段——模拟强化 该阶段的主要任务是查漏补缺,调试身心,增强应试技巧和策略,从知识上弥补前期复习的疏漏,从心理上增强学生的自信心。所以模拟题的难度贴近中考试题,同时多一些创新和猜想,但仅限于极少数试题,不宜给学生造成心理恐慌。因此教师自身也应沉着自信,同时强调学生书写试卷的规范性,防止在不改错的地方失分。谢谢!
同课章节目录
