1.3.2《“杨辉三角”与二项式系数的性质(一)》
文档属性
| 名称 | 1.3.2《“杨辉三角”与二项式系数的性质(一)》 |

|
|
| 格式 | rar | ||
| 文件大小 | 350.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-19 00:00:00 | ||
图片预览




文档简介
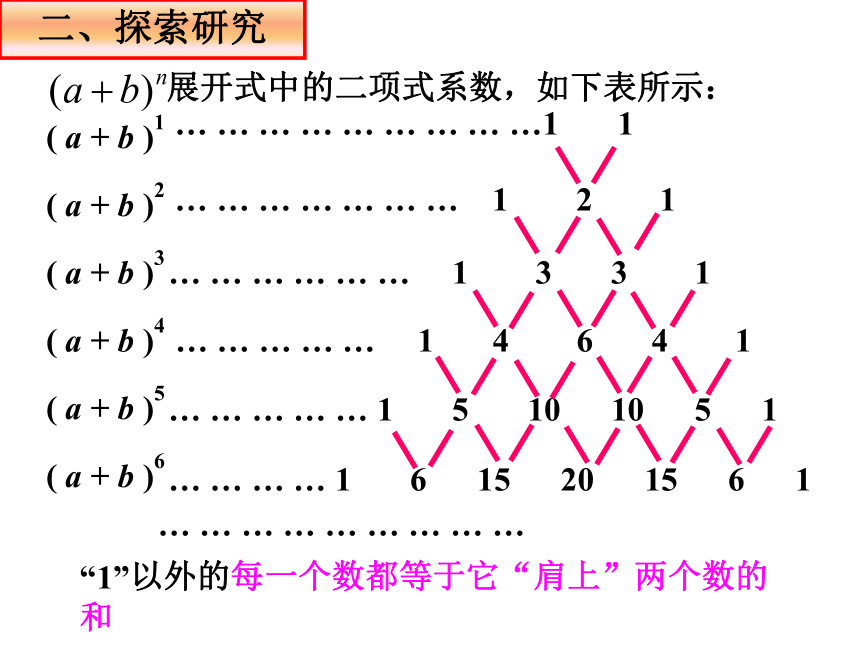
课件27张PPT。1.3.2“杨辉三角”与二项式系数的性质一、朝花夕拾3.二项式系数规律:2.二项展开式的通项:1. 二项式定理 二、探索研究… … … … … … … … …1 1… … … … … … … 1 2 1
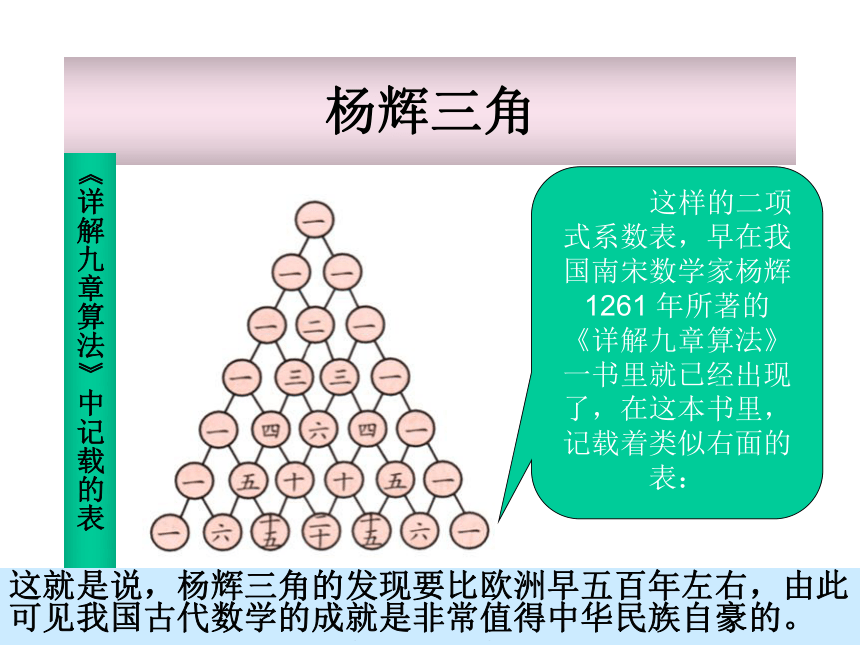
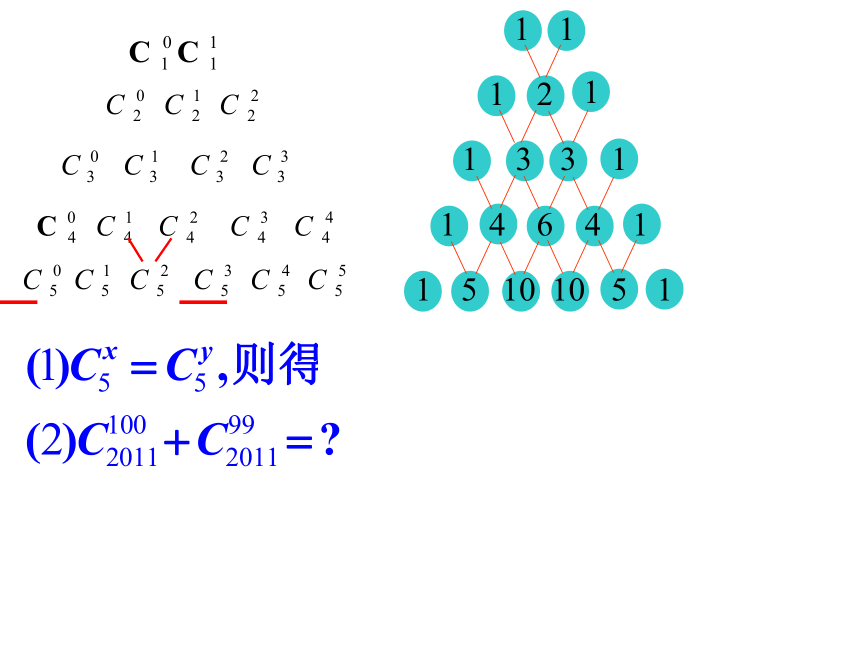
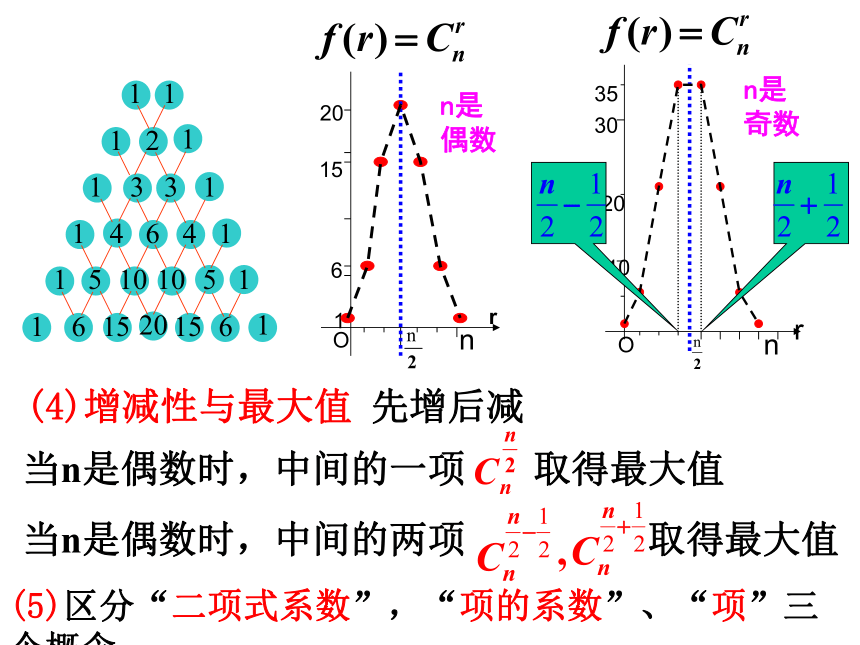
… … … … … … 1 3 3 1… … … … … 1 4 6 4 1… … … … … 1 5 10 10 5 1… … … … 1 6 15 20 15 6 1… … … … … … … … …( a + b )1( a + b )2( a + b )3( a + b )4( a + b )5( a + b )6“1”以外的每一个数都等于它“肩上”两个数的和杨辉三角《九章算术》杨辉杨辉三角《详解九章算法》中记载的表 这样的二项式系数表,早在我国南宋数学家杨辉1261 年所著的
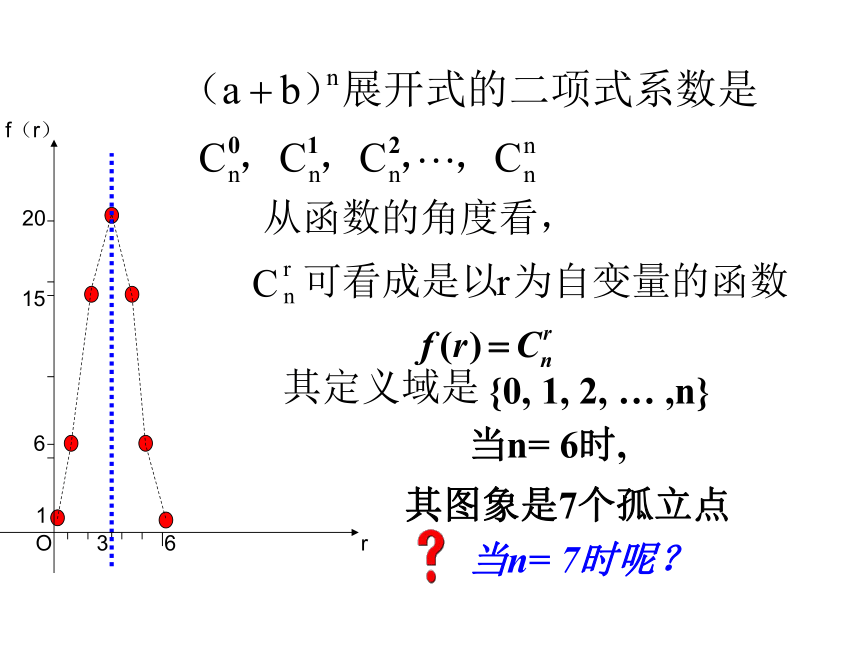
《详解九章算法》一书里就已经出现了,在这本书里,记载着类似右面的表: 在欧洲,人们认为这个表是法国数学家帕斯卡(Blaise Pascal. 1623—1662年)首先发现的,他们把这个表叫做帕斯卡三角。然而,类似这样的表,早在我国宋朝数学家杨辉1261年所著的《详解九章算法》一书里就已出现,我们称它为杨辉三角。杨辉指出此方法出自《释锁》,且我国北宋数学家贾宪(约11世纪)已经用过它。这就是说,杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。1112113311464115101051 当n= 6时,其图象是7个孤立点其定义域是{0, 1, 2, … ,n} 当n= 7时呢?20103035Onrn是偶数n是奇数(4)增减性与最大值 先增后减当n是偶数时,中间的一项 取得最大值当n是偶数时,中间的两项 取得最大值(5)区分“二项式系数”,“项的系数”、“项”三个概念(2)增减性与最大值的证明 二项式系数的增减性由与1的大小决定 二项式系数前半部分是逐渐增大的, 由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 二项式系数的性质(3)各二项式系数的和 证明:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和四、应用性质例1. (1)(1+2x)6展开式中二项式系数最大的项是第 项;(2)(1+2x)7展开式中二项式系数最大的项是第 项;(3)求(1+2x)7展开式中系数最大的项.4(4)求(1-2x)7展开式中系数最大的项和系数最小的项.4、5解: (3), 设第r+1项系数最大, 则故系数最大项为(4)求(1-2x)7展开式中系数最大的项和系数最小的项.分析:,设第r+1项系数最大,则需讨论r的奇偶约分,麻烦!(4)求(1-2x)7展开式中系数最大的项和系数最小的项.解:展开式中系数正负相间,研究系数绝对值由第(3)题可知,r从0到5 ,系数的绝对值增大,r从5到7 ,系数的绝对值减小.故当r=5时,系数最小项为得当r=4时,系数最大项为五、归纳总结(1)对称性 与首末两端“等距离”的两项的二项式系数相等。(2)增减性与最值 先增后减当n是偶数时,中间的一项 取得最大值当n是偶数时,中间的两项 同时取得最大值(3)注意区分“二项式系数”,“项的系数”、“项”三个概念1. 知识点: 2. 数学方法: ——利用不等式研究数列增减性和最值的思想对数列{an},有①{an}递增 ;{an}递减② 若ak是最大项,则若ak是最小项,则 课堂练习:
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ; 例3: 的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项。例4、若 展开式中前三项系数成等差
数列,求(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。2、在(1-x3)(1+x)10的展开式中x5的系数是( )
A.-297 B.-252 C. 297 D. 2073、(x+y+z)9中含x4y2z3的项的系数是__________课堂练习4.已知(1+ )n展开式中含x-2的项的系数为12,求n.
5.已知(10+xlgx)5的展开式中第4项为106,求x的值. 二项展开式中的二项式系数都是一些特殊的组合数,它有三条性质,要理解和掌握好,同时要注意“系数”与“二项式系数”的区别,不能混淆,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项,尤其要理解和掌握“取特值”法,它是解决有关二项展开式系数的问题的重要手段。小结2、在(a+b)10展开式中,二项式系数最大的项是( ).1、在(a+b)20展开式中,与第五项二项式系数相同的项是( ).A课堂练习:A.第6项 B.第7项 C.第6项和第7项 D.第5项和第7项CA.第15项 B.第16项 C.第17项 D.第18项3 (1)已知 展开式中只有第10项系数最大,求第五项;(2)若将“只有第10项”改为“第10项”呢?试求此时n值. 解:由于不含非1常数,展开式的系数即二项式系数(2)若 n 为偶数,同上得n=18若 n 为奇数,则解得n=19或n=173 (1)已知 展开式中只有第10项系数最大,求第五项;(2)若将“只有第10项”改为“第10项”呢?试求此时n值. (1)依题意, n 为偶数,当r=n/2时,系数最大故n=17,n=18或n=19五、施展才华 除了运用组合数公式展开以外,你能利用二项式系数的对称性和增减性,解不等式 吗?解:由C20r对称性和增减性得
… … … … … … 1 3 3 1… … … … … 1 4 6 4 1… … … … … 1 5 10 10 5 1… … … … 1 6 15 20 15 6 1… … … … … … … … …( a + b )1( a + b )2( a + b )3( a + b )4( a + b )5( a + b )6“1”以外的每一个数都等于它“肩上”两个数的和杨辉三角《九章算术》杨辉杨辉三角《详解九章算法》中记载的表 这样的二项式系数表,早在我国南宋数学家杨辉1261 年所著的
《详解九章算法》一书里就已经出现了,在这本书里,记载着类似右面的表: 在欧洲,人们认为这个表是法国数学家帕斯卡(Blaise Pascal. 1623—1662年)首先发现的,他们把这个表叫做帕斯卡三角。然而,类似这样的表,早在我国宋朝数学家杨辉1261年所著的《详解九章算法》一书里就已出现,我们称它为杨辉三角。杨辉指出此方法出自《释锁》,且我国北宋数学家贾宪(约11世纪)已经用过它。这就是说,杨辉三角的发现要比欧洲早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的。1112113311464115101051 当n= 6时,其图象是7个孤立点其定义域是{0, 1, 2, … ,n} 当n= 7时呢?20103035Onrn是偶数n是奇数(4)增减性与最大值 先增后减当n是偶数时,中间的一项 取得最大值当n是偶数时,中间的两项 取得最大值(5)区分“二项式系数”,“项的系数”、“项”三个概念(2)增减性与最大值的证明 二项式系数的增减性由与1的大小决定 二项式系数前半部分是逐渐增大的, 由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值。 二项式系数的性质(3)各二项式系数的和 证明:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和四、应用性质例1. (1)(1+2x)6展开式中二项式系数最大的项是第 项;(2)(1+2x)7展开式中二项式系数最大的项是第 项;(3)求(1+2x)7展开式中系数最大的项.4(4)求(1-2x)7展开式中系数最大的项和系数最小的项.4、5解: (3), 设第r+1项系数最大, 则故系数最大项为(4)求(1-2x)7展开式中系数最大的项和系数最小的项.分析:,设第r+1项系数最大,则需讨论r的奇偶约分,麻烦!(4)求(1-2x)7展开式中系数最大的项和系数最小的项.解:展开式中系数正负相间,研究系数绝对值由第(3)题可知,r从0到5 ,系数的绝对值增大,r从5到7 ,系数的绝对值减小.故当r=5时,系数最小项为得当r=4时,系数最大项为五、归纳总结(1)对称性 与首末两端“等距离”的两项的二项式系数相等。(2)增减性与最值 先增后减当n是偶数时,中间的一项 取得最大值当n是偶数时,中间的两项 同时取得最大值(3)注意区分“二项式系数”,“项的系数”、“项”三个概念1. 知识点: 2. 数学方法: ——利用不等式研究数列增减性和最值的思想对数列{an},有①{an}递增 ;{an}递减② 若ak是最大项,则若ak是最小项,则 课堂练习:
1)已知 ,那么 = ;
2) 的展开式中,二项式系数的最大值是 ;
3)若 的展开式中的第十项和第十一项的二项式系数最大,则n= ; 例3: 的展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项。例4、若 展开式中前三项系数成等差
数列,求(1)展开式中含x的一次幂的项;
(2)展开式中所有x 的有理项;
(3)展开式中系数最大的项。2、在(1-x3)(1+x)10的展开式中x5的系数是( )
A.-297 B.-252 C. 297 D. 2073、(x+y+z)9中含x4y2z3的项的系数是__________课堂练习4.已知(1+ )n展开式中含x-2的项的系数为12,求n.
5.已知(10+xlgx)5的展开式中第4项为106,求x的值. 二项展开式中的二项式系数都是一些特殊的组合数,它有三条性质,要理解和掌握好,同时要注意“系数”与“二项式系数”的区别,不能混淆,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项,尤其要理解和掌握“取特值”法,它是解决有关二项展开式系数的问题的重要手段。小结2、在(a+b)10展开式中,二项式系数最大的项是( ).1、在(a+b)20展开式中,与第五项二项式系数相同的项是( ).A课堂练习:A.第6项 B.第7项 C.第6项和第7项 D.第5项和第7项CA.第15项 B.第16项 C.第17项 D.第18项3 (1)已知 展开式中只有第10项系数最大,求第五项;(2)若将“只有第10项”改为“第10项”呢?试求此时n值. 解:由于不含非1常数,展开式的系数即二项式系数(2)若 n 为偶数,同上得n=18若 n 为奇数,则解得n=19或n=173 (1)已知 展开式中只有第10项系数最大,求第五项;(2)若将“只有第10项”改为“第10项”呢?试求此时n值. (1)依题意, n 为偶数,当r=n/2时,系数最大故n=17,n=18或n=19五、施展才华 除了运用组合数公式展开以外,你能利用二项式系数的对称性和增减性,解不等式 吗?解:由C20r对称性和增减性得
