1.3.1函数的单调性与导函数
文档属性
| 名称 | 1.3.1函数的单调性与导函数 |

|
|
| 格式 | rar | ||
| 文件大小 | 407.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-20 00:00:00 | ||
图片预览








文档简介
课件24张PPT。函数的单调性与导函数学习导数------重在应用单调性的概念对于给定区间I上的函数f(x):
1.如果对于区间I上的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在区间I上是减函数对于函数y=f(x)在某个区间上单调递增或单调递减的性质,叫做f(x)在这个区间上的单调性,这个区间叫做f(x)的单调区间。说明:
1.当函数的单调增区间或减区间有多个时,
单调区间之间不能用 连接,只能分开
写,或者可用“和”连接。2.若单调区间的端点在定义域内,则单调
区间也可以写成闭区间.函数单调性与导数正负的关系 ( 教师说明:)
应正确理解“某个区间”的含义,它必是定义域内的某个区间。在(- ∞ ,0)和
(0, +∞)上分别是减函数。
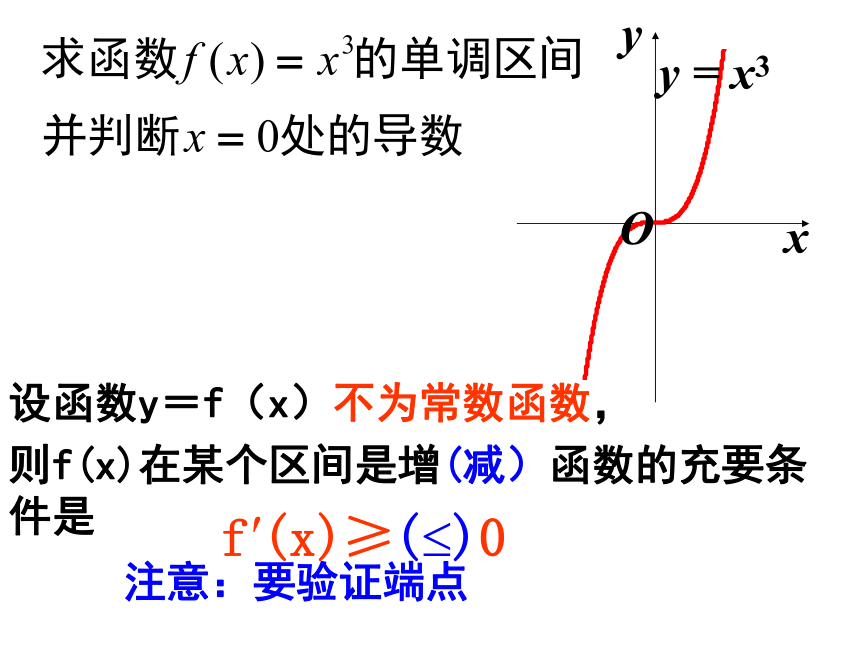
但在定义域上不是减函数。设函数y=f(x)不为常数函数,
则f(x)在某个区间是增(减)函数的充要条件是注意:要验证端点说明:
1、函数 的导数 是函数单调
递增的 条件. 充分不必要3、设函数y=f(x)不为常数函数,则f(x)在
某个区间是增(减)函数的充要条件是注意:要验证端点总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。纳1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?2°试总结用“导数法” 求单调区间的步骤?归已知导函数的下列信息:试画出函数 图象的大致形状。(分析题意后让学生尝试画图,并就学生中出现的两类答案进行投影分析。)2.应用导数信息确定函数大致图象B 变式 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO解: 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.例3.(1)如果函数
在区间 上是减函数,求实数
的取值范围.(2)若函数
是 上的单调函数,则 的取值范围为 .2.已知函数 的单调区间
是 ,则m= .
[解析] 解法一:(区间法)
f′(x)=x2-ax+a-1,令f′(x)=0,所以x=1或x=a-1.
当a-1≤1,即a≤2时,函数f(x)在(1,+∞)内单调递增,不合题意.
当a-1>1,即a>2时,f(x)在(-∞,1)和(a-1,+∞)上单调递增,在(1,a-1)上单调递减,由题意知:(1,4)?(1,a-1)且(6,+∞)?(a-1,+∞),
所以4≤a-1≤6,即5≤a≤7.
解法二:(数形结合)
如图所示,f′(x)=(x-1)[x-(a-1)].若在(1,4)内f′(x)≤0,(6,+∞)内f′(x)≥0,且f′(x)=0有一根为1,则另一根在[4,6]上.解法三:(转化为不等式的恒成立问题)
f′(x)=x2-ax+a-1.因为f(x)在(1,4)内单调递减,所以f′(x)≤0在(1,4)上恒成立.即a(x-1)≥x2-1在(1,4)上恒成立,所以a≥x+1,因为2又因为f(x)在(6,+∞)上单调递增,所以f′(x)≥0在(6,+∞)上恒成立,
所以a≤x+1,因为x+1>7,所以a≤7时,f′(x)≥0在(6,+∞)上恒成立.由题意知5≤a≤7.
[点评] 本题是含参数单调性问题,是高考的重点和热点,体现了数学上的数形结合与转化思想.证明下列不等式证明下列不等式
1.如果对于区间I上的任意两个自变量x1,x2,当x1
1.当函数的单调增区间或减区间有多个时,
单调区间之间不能用 连接,只能分开
写,或者可用“和”连接。2.若单调区间的端点在定义域内,则单调
区间也可以写成闭区间.函数单调性与导数正负的关系 ( 教师说明:)
应正确理解“某个区间”的含义,它必是定义域内的某个区间。在(- ∞ ,0)和
(0, +∞)上分别是减函数。
但在定义域上不是减函数。设函数y=f(x)不为常数函数,
则f(x)在某个区间是增(减)函数的充要条件是注意:要验证端点说明:
1、函数 的导数 是函数单调
递增的 条件. 充分不必要3、设函数y=f(x)不为常数函数,则f(x)在
某个区间是增(减)函数的充要条件是注意:要验证端点总结: 当遇到三次或三次以上的,或图象很难
画出的函数求单调性问题时,应考虑导数法。纳1°什么情况下,用“导数法” 求函数单调性、
单调区间较简便?2°试总结用“导数法” 求单调区间的步骤?归已知导函数的下列信息:试画出函数 图象的大致形状。(分析题意后让学生尝试画图,并就学生中出现的两类答案进行投影分析。)2.应用导数信息确定函数大致图象B 变式 如图, 水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中, 请分别找出与各容器对应的水的高度h与时间t的函数关系图象.(A)(B)(C)(D)htOhtOhtOhtO解: 一般地, 如果一个函数在某一范围内导数的绝对值较大, 那么函数在这个范围内变化得快, 这时, 函数的图象就比较“陡峭”(向上或向下); 反之, 函数的图象就“平缓”一些. 如图,函数 在 或 内的图象“陡峭”,在 或
内的图象平缓.例3.(1)如果函数
在区间 上是减函数,求实数
的取值范围.(2)若函数
是 上的单调函数,则 的取值范围为 .2.已知函数 的单调区间
是 ,则m= .
[解析] 解法一:(区间法)
f′(x)=x2-ax+a-1,令f′(x)=0,所以x=1或x=a-1.
当a-1≤1,即a≤2时,函数f(x)在(1,+∞)内单调递增,不合题意.
当a-1>1,即a>2时,f(x)在(-∞,1)和(a-1,+∞)上单调递增,在(1,a-1)上单调递减,由题意知:(1,4)?(1,a-1)且(6,+∞)?(a-1,+∞),
所以4≤a-1≤6,即5≤a≤7.
解法二:(数形结合)
如图所示,f′(x)=(x-1)[x-(a-1)].若在(1,4)内f′(x)≤0,(6,+∞)内f′(x)≥0,且f′(x)=0有一根为1,则另一根在[4,6]上.解法三:(转化为不等式的恒成立问题)
f′(x)=x2-ax+a-1.因为f(x)在(1,4)内单调递减,所以f′(x)≤0在(1,4)上恒成立.即a(x-1)≥x2-1在(1,4)上恒成立,所以a≥x+1,因为2
所以a≤x+1,因为x+1>7,所以a≤7时,f′(x)≥0在(6,+∞)上恒成立.由题意知5≤a≤7.
[点评] 本题是含参数单调性问题,是高考的重点和热点,体现了数学上的数形结合与转化思想.证明下列不等式证明下列不等式
