2010-2011学年度第二学期九年级第一次摸底考试
文档属性
| 名称 | 2010-2011学年度第二学期九年级第一次摸底考试 |  | |
| 格式 | rar | ||
| 文件大小 | 226.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-21 21:54:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2010-2011学年度第二学期九年级第一次摸底考试
数 学 试 题
命题人:王 辉 2011-3-15
一、选择题(本大题共10小题,每小题4分,满分40分)
1.二次函数y=(2x-1)+2的顶点的坐标是【 】
A.(1,2) B.(1,-2) C.(,2) D.(-,-2)
2. 若函数y = 的自变量x的取值范围是全体实数,则c的取值范围是【 】
A.c<1 B.c=1 C.c>1 D.c≤1
3. 如图,AB//CD,AE//FD,AE、FD分别交BC于点G、H,则图中共有相似三角形【 】.
A.4对 B.5对 C. 6对 D.7对
4.在Rt△ABC中,∠C =90°,sinA =,则cosB的值等于【 】
A. B. C. D.
5.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是…………【 】
A. B. C. D.
6.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是……………………………………………【 】
A.120° B.125° C.135° D.150°
7.如图是由几个小立方块所搭几何体的俯视图 ,小正方形中的数字表示在该位置的小立方块的个数,这个几何体的主视图是【 】
A B C D
8.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得,在C点测得,又测得米,则小岛B到公路l的距离为【 】
A.25 B. C. D.
9. 如图,在图 1所示的正方形铁皮上剪下一个圆形和扇形,使之恰好围成图2所示的一个圆锥模型.设圆的半径为,扇形的半径为 ( http: / / www.21cnjy.com / ),则圆的半径与扇形的半径之间的关系为……………………………………………【 】
A. B. ( http: / / www.21cnjy.com / ) C. D. ( http: / / www.21cnjy.com / )
10.从2,3,4,5这四个数中,任取两个数和(≠),构成函数和,使两个函数图象的交点在直线=2的左侧,则这样的有序数组(,)共有【 】
A.4组 B.5组 C.6组 D.不确定
二、填空题(本大题共4小题,每小题5分,满分20分)
11.锐角满足,则___________.
12、如图,在同心圆中,大圆的弦AB切小圆于点C,
AB=8,则圆环的面积是 .
13.如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥
体而得到的,其底面直径AB =,高BC =,求这个零件的表面积 (结果保留)
14.已知二次函数的图象经过原点及点(,),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析
式为 .
三.(本大题共2小题,每小题8分,满分16分)
15. 计算:
16.如图,已知AB是⊙O的直径,点C是⊙O上一点,连结BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连结BF,与直线CD交于点G.求证:BC2=BG·BF
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,A、B两点在函数的图象上.
(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数。
18如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1) 求钢缆CD的长度;
(2) 若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
五、(本大题共2小题,每小题10分,满分20分)
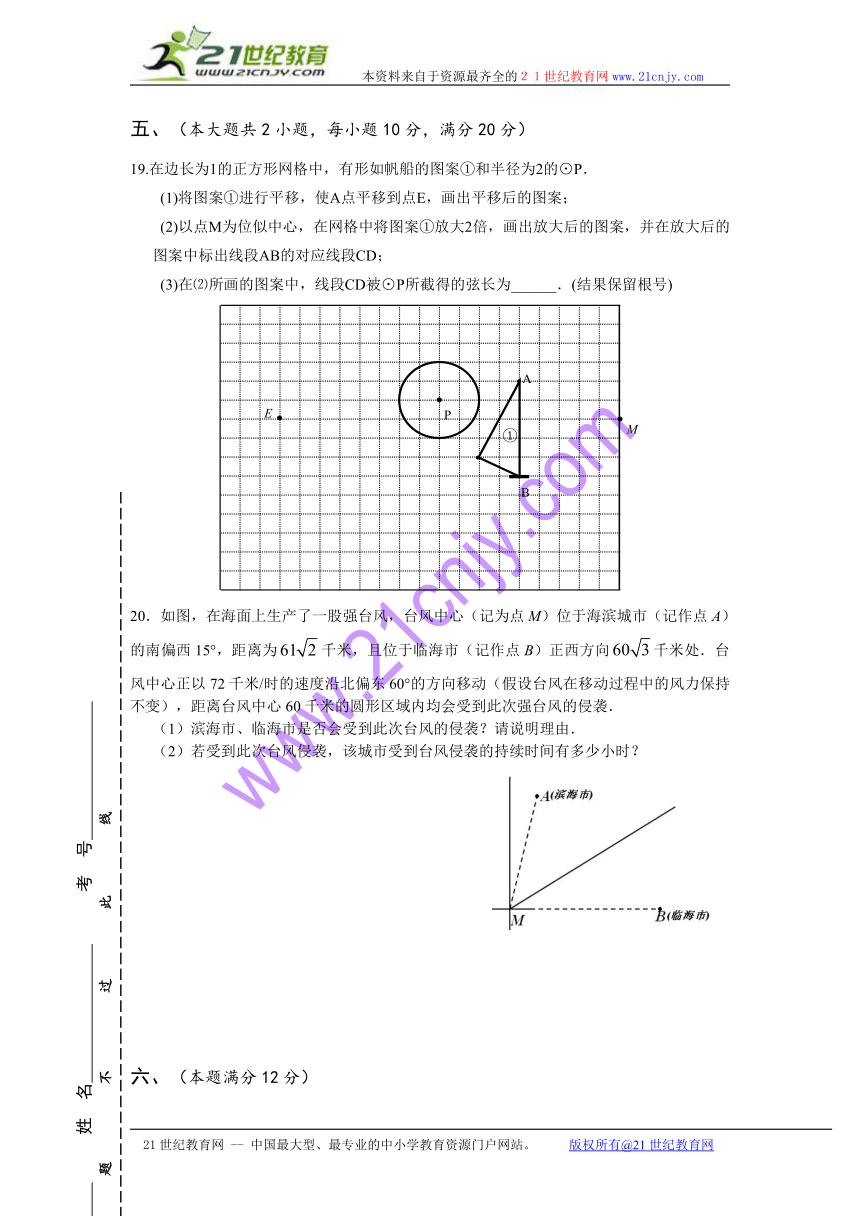
19.在边长为1的正方形网格中,有形如帆船的图案①和半径为2的⊙P.
(1)将图案①进行平移,使A点平移到点E,画出平移后的图案;
(2)以点M为位似中心,在网格中将图案①放大2倍,画出放大后的图案,并在放大后的图案中标出线段AB的对应线段CD;
(3)在⑵所画的图案中,线段CD被⊙P所截得的弦长为______.(结果保留根号)
20.如图,在海面上生产了一股强台风,台风中心(记为点M)位于海滨城市(记作点A)的南偏西15°,距离为千米,且位于临海市(记作点B)正西方向千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
六、(本题满分12分)
21.甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
七、(本题满分12分)
22.如图,点在⊙O上,,与相交于点,,延长到点,使,连结.
(1)证明;
(2)试判断直线与⊙O的位置关系,并给出证明.
八、(本题满分14分)
23、如图1,已知抛物线的顶点为A(O,1),矩形CDEF的顶点C、F在抛物线上,D、E在轴上,CF交y轴于点B(0,2),且其面为8.
(1)求此抛物线的解析式;
(2)如图2,若P点为抛物线上不同于
A的一点,连结PB并延长交抛物线
于点Q,过点P、Q分别作轴的垂线,
垂足分别为S、R.
1 求证:PB=PS;
2 判断△SBR的形状;
③ 试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似,若存在,请找出M点的位置;若不存在,请说明理由.
数学参考答案
1 2 3 4 5 6 7 8 9 10
C C C B B C D B D B
11、75 12、16 13 、168 14.,
15解:原式= -1 ...............5分
= -1
=-7 .............................8分
16. .证明:∵AB是⊙O的直径,∠ACB=90°,又CD⊥AB于D,∴∠BCD=∠A,又∠A=∠F,∴∠F=∠BCD=∠BCG,在△BCG和△BFC中,∴△BCG∽△BFC…………6′
∴
即…………8′
18、(1) 在中,
设则
∵ ∴
∴…………………………………………………………4分
(2)
过E作EF垂直于BC交于点F,过A作AG垂直于EF交于点G,
由题意有AB=GF=8
在中,,AE=1.6米,∴EG=0..8米
∴EF=9米。………………………………………………………………8分
19.解: ⑴平移后的图案,如图所示;⑵放大后的图案,如图所示;
⑶线段CD被⊙P所截得的弦长为. (每小题分别为3分、3分、4分,共10分)
20. 解:(1)设台风中心运行的路线为射线MN,于是∠MAN=60°-15°=45°,
过A作AH⊥MN于H,故AMH是等腰直角三角形
∵∴AH=61>60∴滨海市不会受到台风的影响;………………5′
(2)过B作BH1⊥MN于H1,∵,
∠BMN=90°-60°=30°
∴,因此临海市会受到台风的影响;以B为圆心60为半径作圆与MN交于T1、T2,则BT1=BT2=60
在中,∴∴△B T1T2是等边三角形………7′
∴T1T2=60
∴台风中心经过线段T1T2上所用的时间小时,
因此临海市受到台风侵袭的时间为小时。……………10′
21.解:(1)若甲先摸,共有15张卡片可供选择,其中写有“石头”的卡片共3张,
故甲摸出“石头”的概率为.………………3分
(2)若甲先摸且摸出“石头”,则可供乙选择的卡片还有14张,其中乙只有摸出卡片“锤子”
或“布”才能获胜,这样的卡片共有8张,故乙获胜的概率为. ……6分
(3)若甲先摸,则“锤子”、“石头”、“剪子”、“布”四种卡片都有可能被摸出.
若甲先摸出“锤子”,则甲获胜(即乙摸出“石头”或“剪子”)的概率为;……7分
若甲先摸出“石头”,则甲获胜(即乙摸出“剪子”)的概率为; ……8分
若甲先摸出“剪子”,则甲获胜(即乙摸出“布”)的概率为; ……9分
若甲先摸出“布”,则甲获胜(即乙摸出“锤子”或“石头”)的概率为. ……10分
故甲先摸出“锤子”获胜的可能性最大. ……12分
22.(1)证明:(1)在和中,
,,.……3分
又,
. 5分
(2)直线与⊙O相切. 6分
证明:连结.
, …………7分
. …………8分
. …………9分
所以是等腰三角形顶角的平分线.
. …………10分
由,得..…………11分
由知,.直线与⊙O相切. …………12分
23.⑴解:∵B点坐标为(0.2),∴OB=2,
∵矩形CDEF面积为8,∴CF=4.
∴C点坐标为(一2,2).F点坐标为(2,2)。
设抛物线的解析式为.其过三点A(0,1),C(-2.2),F(2,2)。
得
解这个方程组,得
∴此抛物线的解析式为 …… (4分)
(2)解:①过点B作BN,垂足为N.
∵P点在抛物线y=十l上.可设P点坐标为.
∴PS=,OB=NS=2,BN=。
∴PN=PS—NS= ………………………… (6分)
在Rt△PNB中.
PB2=
∴PB=PS=………………………… (7分)
②根据①同理可知BQ=QR。
∴,
又∵ ,
∴,
同理SBP=
∴
∴
∴.
∴ △SBR为直角三角形.………………………… (10分)
③ 若以P、S、M为顶点的三角形与以Q、M、R为顶点的三角形相似,
∵,
∴有PSM∽MRQ和PSM∽△QRM两种情况。
当PSM∽MRQ时.SPM=RMQ,SMP=RQM.
由直角三角形两锐角互余性质.知PMS+QMR=。
∴。
取PQ中点为N.连结MN.则MN=PQ=
∴MN为直角梯形SRQP的中位线,
∴点M为SR的中点…………………(12分)
当△PSM∽△QRM时,
又,即M点与O点重合。
∴点M为原点O。
综上所述,当点M为SR的中点时,PSM∽△MRQ;
当点M为原点时,PSM∽△QRM …………(14分)
班 级 姓 名 考 号
答 题 不 过 此 线
第3题图
1
1
1
2
B
C
A
D
l
图1
图2
第 9题图
第8题图
第12题图
13题图
8题图
3题图
A
D
C
B
E
M
A
E
B
P
①
班 级 姓 名 考 号
答 题 不 过 此 线
A
C
D
O
E
F
B
图二
图一
E
M
A
B
P
D
C
第22题图
c
M
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2010-2011学年度第二学期九年级第一次摸底考试
数 学 试 题
命题人:王 辉 2011-3-15
一、选择题(本大题共10小题,每小题4分,满分40分)
1.二次函数y=(2x-1)+2的顶点的坐标是【 】
A.(1,2) B.(1,-2) C.(,2) D.(-,-2)
2. 若函数y = 的自变量x的取值范围是全体实数,则c的取值范围是【 】
A.c<1 B.c=1 C.c>1 D.c≤1
3. 如图,AB//CD,AE//FD,AE、FD分别交BC于点G、H,则图中共有相似三角形【 】.
A.4对 B.5对 C. 6对 D.7对
4.在Rt△ABC中,∠C =90°,sinA =,则cosB的值等于【 】
A. B. C. D.
5.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是…………【 】
A. B. C. D.
6.△ABC中,AB=AC,∠A为锐角,CD为AB边上的高,I为△ACD的内切圆圆心,则∠AIB的度数是……………………………………………【 】
A.120° B.125° C.135° D.150°
7.如图是由几个小立方块所搭几何体的俯视图 ,小正方形中的数字表示在该位置的小立方块的个数,这个几何体的主视图是【 】
A B C D
8.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得,在C点测得,又测得米,则小岛B到公路l的距离为【 】
A.25 B. C. D.
9. 如图,在图 1所示的正方形铁皮上剪下一个圆形和扇形,使之恰好围成图2所示的一个圆锥模型.设圆的半径为,扇形的半径为 ( http: / / www.21cnjy.com / ),则圆的半径与扇形的半径之间的关系为……………………………………………【 】
A. B. ( http: / / www.21cnjy.com / ) C. D. ( http: / / www.21cnjy.com / )
10.从2,3,4,5这四个数中,任取两个数和(≠),构成函数和,使两个函数图象的交点在直线=2的左侧,则这样的有序数组(,)共有【 】
A.4组 B.5组 C.6组 D.不确定
二、填空题(本大题共4小题,每小题5分,满分20分)
11.锐角满足,则___________.
12、如图,在同心圆中,大圆的弦AB切小圆于点C,
AB=8,则圆环的面积是 .
13.如图,这是一个由圆柱体材料加工而成的零件,它是以圆柱体的上底面为底面,在其内部“掏取”一个与圆柱体等高的圆锥
体而得到的,其底面直径AB =,高BC =,求这个零件的表面积 (结果保留)
14.已知二次函数的图象经过原点及点(,),且图象与x轴的另一交点到原点的距离为1,则该二次函数的解析
式为 .
三.(本大题共2小题,每小题8分,满分16分)
15. 计算:
16.如图,已知AB是⊙O的直径,点C是⊙O上一点,连结BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连结BF,与直线CD交于点G.求证:BC2=BG·BF
四、(本大题共2小题,每小题8分,满分16分)
17. 如图,A、B两点在函数的图象上.
(1)求的值及直线AB的解析式;
(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数。
18如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1) 求钢缆CD的长度;
(2) 若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
五、(本大题共2小题,每小题10分,满分20分)
19.在边长为1的正方形网格中,有形如帆船的图案①和半径为2的⊙P.
(1)将图案①进行平移,使A点平移到点E,画出平移后的图案;
(2)以点M为位似中心,在网格中将图案①放大2倍,画出放大后的图案,并在放大后的图案中标出线段AB的对应线段CD;
(3)在⑵所画的图案中,线段CD被⊙P所截得的弦长为______.(结果保留根号)
20.如图,在海面上生产了一股强台风,台风中心(记为点M)位于海滨城市(记作点A)的南偏西15°,距离为千米,且位于临海市(记作点B)正西方向千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
六、(本题满分12分)
21.甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
七、(本题满分12分)
22.如图,点在⊙O上,,与相交于点,,延长到点,使,连结.
(1)证明;
(2)试判断直线与⊙O的位置关系,并给出证明.
八、(本题满分14分)
23、如图1,已知抛物线的顶点为A(O,1),矩形CDEF的顶点C、F在抛物线上,D、E在轴上,CF交y轴于点B(0,2),且其面为8.
(1)求此抛物线的解析式;
(2)如图2,若P点为抛物线上不同于
A的一点,连结PB并延长交抛物线
于点Q,过点P、Q分别作轴的垂线,
垂足分别为S、R.
1 求证:PB=PS;
2 判断△SBR的形状;
③ 试探索在线段SR上是否存在点M,使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似,若存在,请找出M点的位置;若不存在,请说明理由.
数学参考答案
1 2 3 4 5 6 7 8 9 10
C C C B B C D B D B
11、75 12、16 13 、168 14.,
15解:原式= -1 ...............5分
= -1
=-7 .............................8分
16. .证明:∵AB是⊙O的直径,∠ACB=90°,又CD⊥AB于D,∴∠BCD=∠A,又∠A=∠F,∴∠F=∠BCD=∠BCG,在△BCG和△BFC中,∴△BCG∽△BFC…………6′
∴
即…………8′
18、(1) 在中,
设则
∵ ∴
∴…………………………………………………………4分
(2)
过E作EF垂直于BC交于点F,过A作AG垂直于EF交于点G,
由题意有AB=GF=8
在中,,AE=1.6米,∴EG=0..8米
∴EF=9米。………………………………………………………………8分
19.解: ⑴平移后的图案,如图所示;⑵放大后的图案,如图所示;
⑶线段CD被⊙P所截得的弦长为. (每小题分别为3分、3分、4分,共10分)
20. 解:(1)设台风中心运行的路线为射线MN,于是∠MAN=60°-15°=45°,
过A作AH⊥MN于H,故AMH是等腰直角三角形
∵∴AH=61>60∴滨海市不会受到台风的影响;………………5′
(2)过B作BH1⊥MN于H1,∵,
∠BMN=90°-60°=30°
∴,因此临海市会受到台风的影响;以B为圆心60为半径作圆与MN交于T1、T2,则BT1=BT2=60
在中,∴∴△B T1T2是等边三角形………7′
∴T1T2=60
∴台风中心经过线段T1T2上所用的时间小时,
因此临海市受到台风侵袭的时间为小时。……………10′
21.解:(1)若甲先摸,共有15张卡片可供选择,其中写有“石头”的卡片共3张,
故甲摸出“石头”的概率为.………………3分
(2)若甲先摸且摸出“石头”,则可供乙选择的卡片还有14张,其中乙只有摸出卡片“锤子”
或“布”才能获胜,这样的卡片共有8张,故乙获胜的概率为. ……6分
(3)若甲先摸,则“锤子”、“石头”、“剪子”、“布”四种卡片都有可能被摸出.
若甲先摸出“锤子”,则甲获胜(即乙摸出“石头”或“剪子”)的概率为;……7分
若甲先摸出“石头”,则甲获胜(即乙摸出“剪子”)的概率为; ……8分
若甲先摸出“剪子”,则甲获胜(即乙摸出“布”)的概率为; ……9分
若甲先摸出“布”,则甲获胜(即乙摸出“锤子”或“石头”)的概率为. ……10分
故甲先摸出“锤子”获胜的可能性最大. ……12分
22.(1)证明:(1)在和中,
,,.……3分
又,
. 5分
(2)直线与⊙O相切. 6分
证明:连结.
, …………7分
. …………8分
. …………9分
所以是等腰三角形顶角的平分线.
. …………10分
由,得..…………11分
由知,.直线与⊙O相切. …………12分
23.⑴解:∵B点坐标为(0.2),∴OB=2,
∵矩形CDEF面积为8,∴CF=4.
∴C点坐标为(一2,2).F点坐标为(2,2)。
设抛物线的解析式为.其过三点A(0,1),C(-2.2),F(2,2)。
得
解这个方程组,得
∴此抛物线的解析式为 …… (4分)
(2)解:①过点B作BN,垂足为N.
∵P点在抛物线y=十l上.可设P点坐标为.
∴PS=,OB=NS=2,BN=。
∴PN=PS—NS= ………………………… (6分)
在Rt△PNB中.
PB2=
∴PB=PS=………………………… (7分)
②根据①同理可知BQ=QR。
∴,
又∵ ,
∴,
同理SBP=
∴
∴
∴.
∴ △SBR为直角三角形.………………………… (10分)
③ 若以P、S、M为顶点的三角形与以Q、M、R为顶点的三角形相似,
∵,
∴有PSM∽MRQ和PSM∽△QRM两种情况。
当PSM∽MRQ时.SPM=RMQ,SMP=RQM.
由直角三角形两锐角互余性质.知PMS+QMR=。
∴。
取PQ中点为N.连结MN.则MN=PQ=
∴MN为直角梯形SRQP的中位线,
∴点M为SR的中点…………………(12分)
当△PSM∽△QRM时,
又,即M点与O点重合。
∴点M为原点O。
综上所述,当点M为SR的中点时,PSM∽△MRQ;
当点M为原点时,PSM∽△QRM …………(14分)
班 级 姓 名 考 号
答 题 不 过 此 线
第3题图
1
1
1
2
B
C
A
D
l
图1
图2
第 9题图
第8题图
第12题图
13题图
8题图
3题图
A
D
C
B
E
M
A
E
B
P
①
班 级 姓 名 考 号
答 题 不 过 此 线
A
C
D
O
E
F
B
图二
图一
E
M
A
B
P
D
C
第22题图
c
M
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
