3.2.3三角形的内切圆
图片预览




文档简介
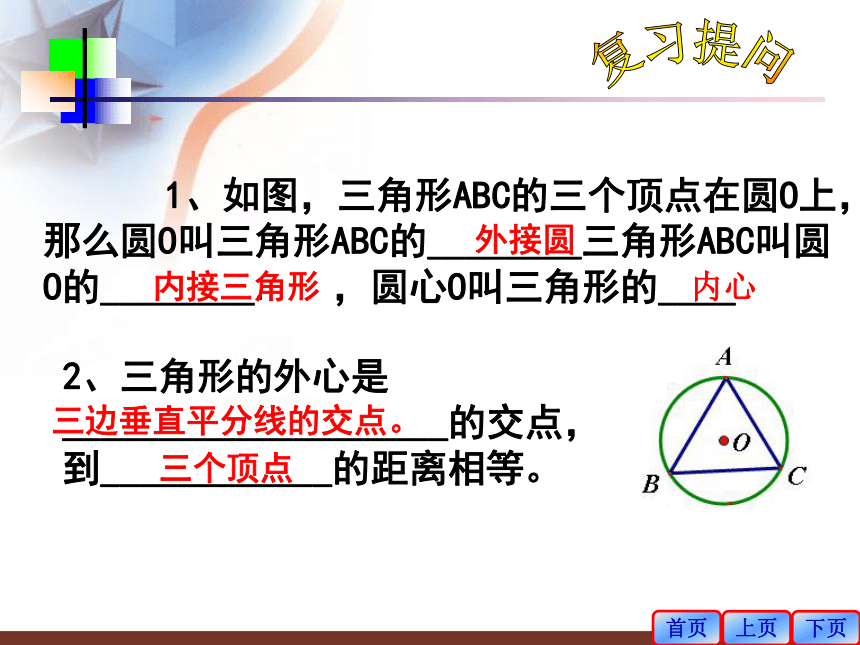
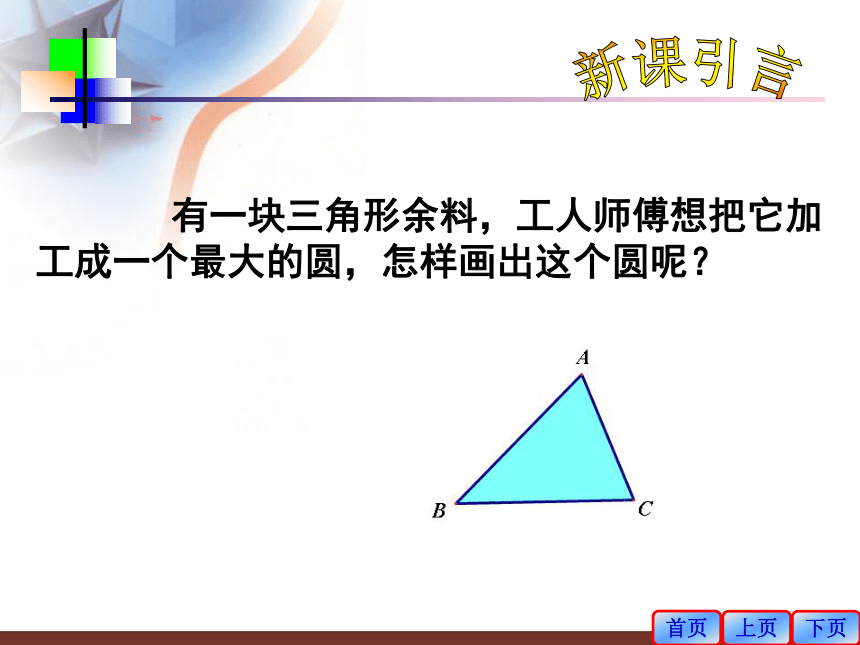
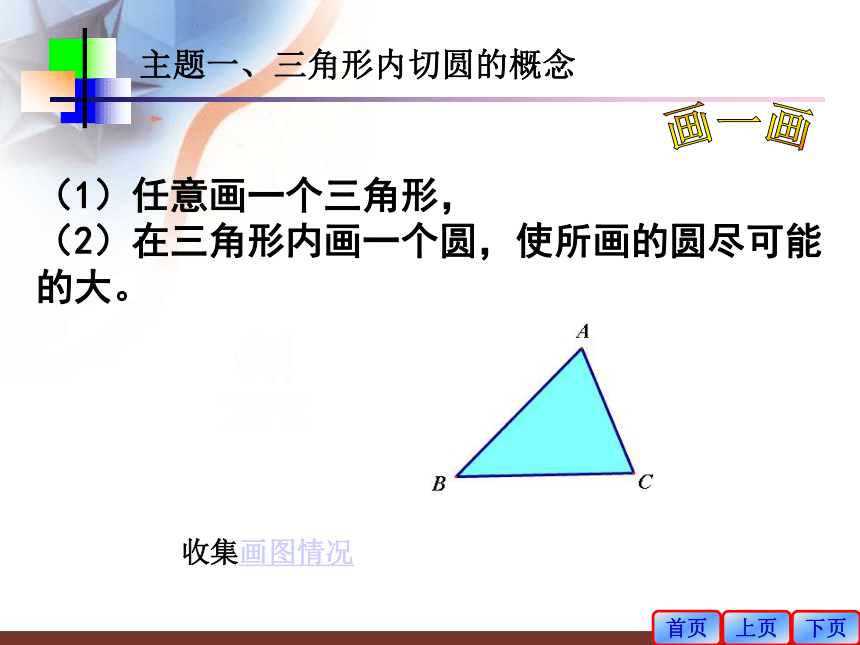
课件16张PPT。 3.2.3三角形的内切圆湖南省新邵县酿溪中学王军旗复习提问 1、如图,三角形ABC的三个顶点在圆O上,那么圆O叫三角形ABC的________三角形ABC叫圆O的________. ,圆心O叫三角形的____首页上页下页外接圆内接三角形2、三角形的外心是____________________的交点,到____________的距离相等。三边垂直平分线的交点。三个顶点内心新课引言 有一块三角形余料,工人师傅想把它加工成一个最大的圆,怎样画出这个圆呢?首页上页下页画一画(1)任意画一个三角形,
(2)在三角形内画一个圆,使所画的圆尽可能的大。首页下页上页收集画图情况主题一、三角形内切圆的概念三角形中最大的圆是怎样画出来的?1、圆心的位置怎么确定? 由于△ABC的三边都与圆相切,所以圆心到三边的距离都等于__________,从而这些距离相等,我们已经知道,到一个角的两边的距离相等的点在这个角的平分线上,因此圆心O是∠A,∠B的______________________半径平分线的交点。2、半径怎么确定? 过O点作OM⊥AB于M,则OM的长就是圆的半径。OM想一想作法: 1、作∠A、∠B的平分线AD,BE,它们相交于点O;
2、过点O作AB的垂线,垂足为M;
3、以点O为圆心,OM为半径作圆。
圆O就是所求的圆。MO3、这样做出来的圆与三角形的三边一定都相切吗?∵圆心O到AB的距离等于OM的长,而OM就是⊙O的半径,
∴AB与⊙O相切。
∵点O在∠A,∠B的平分线上,∴O点到AB,AC,BC的距离相等,都等于半径OM, ∴⊙O与△ABC的三边都相切。
4、与△ABC三边都相切的圆有几个? 由于圆心O是∠ A,∠B的平分线的交点,两条直线相交只有一个交点,所以圆心只有一个,而半径是O到AB的距离OM,OM的长度也是唯一的。所以和三角形三边都相切的圆只有一个。与三角形三边都相切的圆有且只有一个(1)与三角形三边都相切的圆叫___________。这个三角形叫这个圆的__________。
(2)内切圆的圆心叫三角形的__________。
三角形的内切圆外切三角形内心思考:1、观察下图,三角形ABC与⊙O的位置有什么特点?根据这个特点填空。2、三角形 内心有什么特点?三角形的内心是_______________的交点,到________的距离相等。三角形角平分线三边主题二 、应用例1.设△ABC的内切圆的半径为r,△ABC的周长为l,求三角形ABC的面积。
【分析】由于不知道底边和高,所以无法用“底×高”求三角形的面积,因此需要考虑内切圆的半径与周长和面积有什么关系。DEF【解】设AB,BC,AC分别与⊙O交于点D,E,F,连接OA,OB,OC,OD,OE,OF,则OD⊥AB,OE⊥BC,OF⊥AC解:连接OE,OF,
∵AB切⊙O于E,AC切⊙O于F,
∴OE⊥AB,OF⊥AC,
∵∠EDF=60o,
∴∠EOF=2∠EDF=120o
∴∠A=360o-2×90o-120o=60o
例2.如图⊙O内切于△ABC三边,切点分别是E、D、F,且∠EDF=60o,求∠A的度数。【例3】.已知I为△ABC的内心,且∠ABC=40o,∠ACB=70o,求∠BIC的度数。 【解】
∵I是△ABC的内心,∴∠IBC=0.5∠ABC=20 o,∠ICB=0.5∠ACB=35 o
∴∠ BIC=180 o-∠IBC-∠ICB
=180 o-20 o-35 o=125 o
变式练习1、已知正三角形的边长为2,则它的内切圆和外接圆组成的圆环面积为( )
A 0.5 ,B C 2 D 3【解】如图,
S圆环=π(OB2-OF2) =πBF2=π×12=π,
选B
2、一个三角形的一个角的平分线与对边的交点是不是这条边与内切圆的交点呢? 【答】不一定,如图,BE是△ABC的角平分线,但E点不是内切圆与AC的交点。3、等边三角形的一个角平分线与对边的交点是不是这条边与内切圆的切点呢? 【答】是的
如图,BD是∠ABC的平分线,
交AC于D,O点是内心,若D
不是切点,设切点为F,连
接OF,则OF⊥AC,由等腰三
角形“三线合一”知,BD⊥AC,所以过点O有就两条直线和AC垂直,这和“过直线外的一点有且只有一条直线和已知直线垂直”矛盾。所以D是⊙O的切点。4、任意一个三角形的外接圆和内切圆是同心圆吗?【答】如图,△ABC的内切圆和外接圆就不是同心圆。小结作业P80 A 4—8 B 2,3
(2)在三角形内画一个圆,使所画的圆尽可能的大。首页下页上页收集画图情况主题一、三角形内切圆的概念三角形中最大的圆是怎样画出来的?1、圆心的位置怎么确定? 由于△ABC的三边都与圆相切,所以圆心到三边的距离都等于__________,从而这些距离相等,我们已经知道,到一个角的两边的距离相等的点在这个角的平分线上,因此圆心O是∠A,∠B的______________________半径平分线的交点。2、半径怎么确定? 过O点作OM⊥AB于M,则OM的长就是圆的半径。OM想一想作法: 1、作∠A、∠B的平分线AD,BE,它们相交于点O;
2、过点O作AB的垂线,垂足为M;
3、以点O为圆心,OM为半径作圆。
圆O就是所求的圆。MO3、这样做出来的圆与三角形的三边一定都相切吗?∵圆心O到AB的距离等于OM的长,而OM就是⊙O的半径,
∴AB与⊙O相切。
∵点O在∠A,∠B的平分线上,∴O点到AB,AC,BC的距离相等,都等于半径OM, ∴⊙O与△ABC的三边都相切。
4、与△ABC三边都相切的圆有几个? 由于圆心O是∠ A,∠B的平分线的交点,两条直线相交只有一个交点,所以圆心只有一个,而半径是O到AB的距离OM,OM的长度也是唯一的。所以和三角形三边都相切的圆只有一个。与三角形三边都相切的圆有且只有一个(1)与三角形三边都相切的圆叫___________。这个三角形叫这个圆的__________。
(2)内切圆的圆心叫三角形的__________。
三角形的内切圆外切三角形内心思考:1、观察下图,三角形ABC与⊙O的位置有什么特点?根据这个特点填空。2、三角形 内心有什么特点?三角形的内心是_______________的交点,到________的距离相等。三角形角平分线三边主题二 、应用例1.设△ABC的内切圆的半径为r,△ABC的周长为l,求三角形ABC的面积。
【分析】由于不知道底边和高,所以无法用“底×高”求三角形的面积,因此需要考虑内切圆的半径与周长和面积有什么关系。DEF【解】设AB,BC,AC分别与⊙O交于点D,E,F,连接OA,OB,OC,OD,OE,OF,则OD⊥AB,OE⊥BC,OF⊥AC解:连接OE,OF,
∵AB切⊙O于E,AC切⊙O于F,
∴OE⊥AB,OF⊥AC,
∵∠EDF=60o,
∴∠EOF=2∠EDF=120o
∴∠A=360o-2×90o-120o=60o
例2.如图⊙O内切于△ABC三边,切点分别是E、D、F,且∠EDF=60o,求∠A的度数。【例3】.已知I为△ABC的内心,且∠ABC=40o,∠ACB=70o,求∠BIC的度数。 【解】
∵I是△ABC的内心,∴∠IBC=0.5∠ABC=20 o,∠ICB=0.5∠ACB=35 o
∴∠ BIC=180 o-∠IBC-∠ICB
=180 o-20 o-35 o=125 o
变式练习1、已知正三角形的边长为2,则它的内切圆和外接圆组成的圆环面积为( )
A 0.5 ,B C 2 D 3【解】如图,
S圆环=π(OB2-OF2) =πBF2=π×12=π,
选B
2、一个三角形的一个角的平分线与对边的交点是不是这条边与内切圆的交点呢? 【答】不一定,如图,BE是△ABC的角平分线,但E点不是内切圆与AC的交点。3、等边三角形的一个角平分线与对边的交点是不是这条边与内切圆的切点呢? 【答】是的
如图,BD是∠ABC的平分线,
交AC于D,O点是内心,若D
不是切点,设切点为F,连
接OF,则OF⊥AC,由等腰三
角形“三线合一”知,BD⊥AC,所以过点O有就两条直线和AC垂直,这和“过直线外的一点有且只有一条直线和已知直线垂直”矛盾。所以D是⊙O的切点。4、任意一个三角形的外接圆和内切圆是同心圆吗?【答】如图,△ABC的内切圆和外接圆就不是同心圆。小结作业P80 A 4—8 B 2,3
