概率2
图片预览








文档简介
课件31张PPT。25.1.2概率的意义 概率论的产生和发展
概率论产生于十七世纪,本来是由保险事业的发展而产生的,但是来自于赌博者的请求,却是数学家们思考概率论问题的源泉。
传说早在1654年,有一个赌徒梅累向当时的数学家帕斯卡提出一个使他苦恼了很久的问题:“两个赌徒相约赌若干局,谁先赢 3局就算赢,全部赌本就归谁。但是当其中一个人赢了 2局,另一个人赢了1局的时候,由于某种原因,赌博终止了。问:赌本应该如何分法才合理?”
帕斯卡是17世纪著名的数学家,但这个问题却让他苦苦思索了三年,三年后,也就是1657年,荷兰著名的数学家惠更斯企图自己解决这一问题,结果写成了《论赌博中的计算》一书,这就是概率论最早的一部著作。
近几十年来,随着科技的蓬勃发展,概率论大量应用到国民经济、工农业生产及各学科领域。许多兴起的应用数学,如信息论、对策论、排队论、控制论等,都是以概率论作为基础的。
指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是随机事件?(2)手电筒的电池没电,灯泡发亮.(5)当 x 是实数时,x2 ≥ 0; (6)一个袋内装有形状大小相同的一个白球和一个黑球,从中任意摸出1个球则为白球. (3)在标准大气压下,水在温度 时沸腾;(4)直线 过定点 ;(1)某地1月1日刮西北风;(7)、打开电视机,正在播广告;
(8)、我区每年都会下雨;
(9)、明天的太阳从西方升起来;
(10)、掷两个骰子两个6朝上;
(11)、异号两数相乘,积为正数;
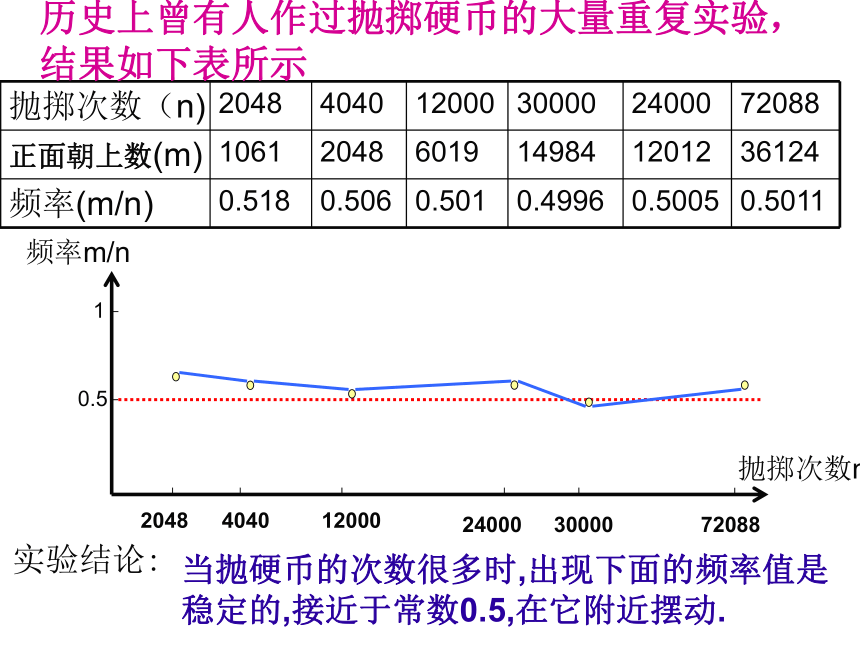
(12)、某种电器工作时,机身发热;探究:投掷硬币时,国徽朝上的可能性有多大?在同样条件下,随机事件可能发生,也可能不发生,那么它发生的可能性有多大呢?这是我们下面要讨论的问题。历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示实验结论:当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动. 随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
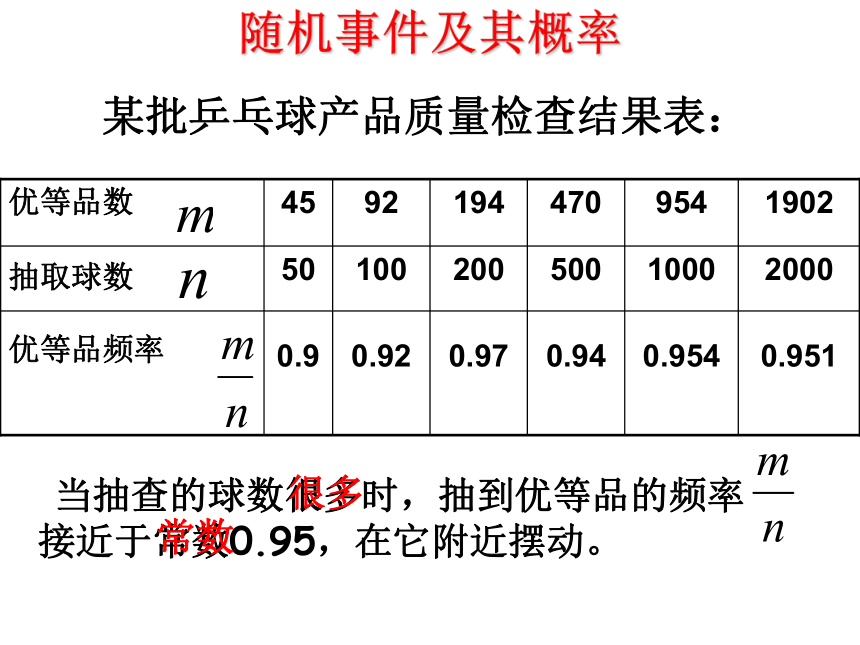
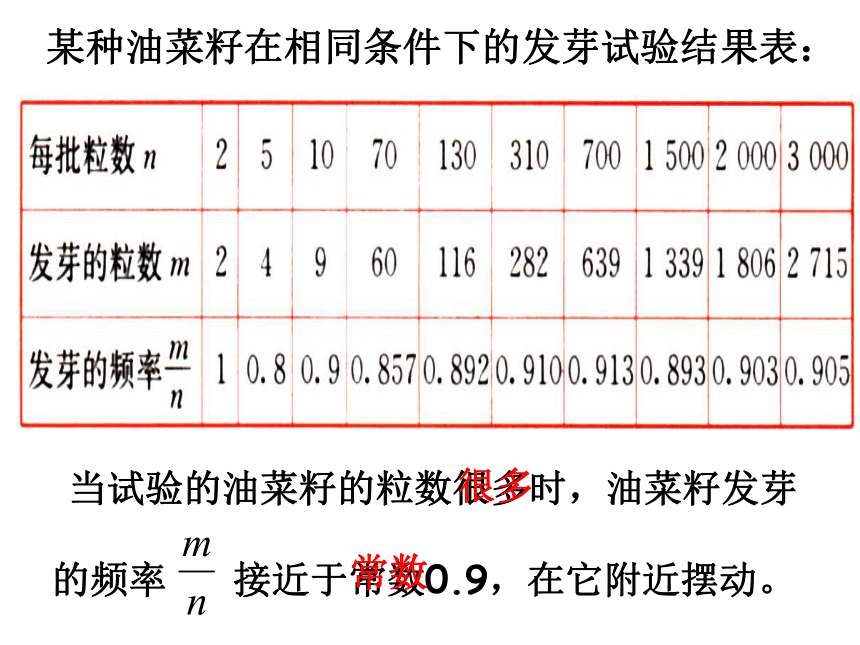
生呈现出一定的规律性.出现的频率值接近于常数.随机事件及其概率某批乒乓球产品质量检查结果表: 当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。 很多常数某种油菜籽在相同条件下的发芽试验结果表: 当试验的油菜籽的粒数很多时,油菜籽发芽
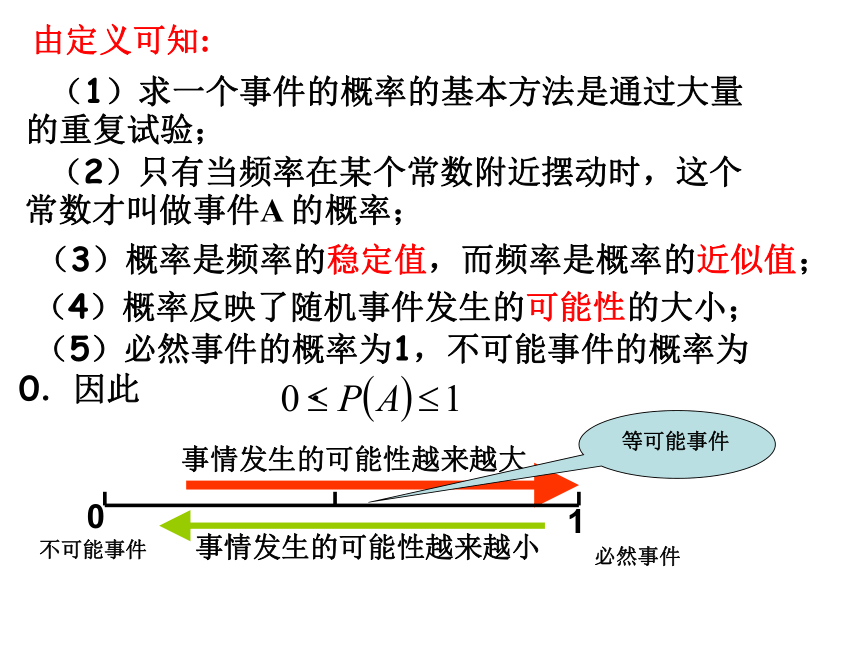
的频率 接近于常数0.9,在它附近摆动。很多 常数随机事件及其概率事件 的概率的定义: 一般地,在大量重复进行同一试验时,事件 发生的频率 (n为实验的次数,m是事件发生的频数)总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率,记做 . 事件一般用大写英文字母A,B,C,...表示 事件发生的可能性越大,则它的概率越接近1;事件发生的可能性越小,则它的概率越接近0.由定义可知: (1)求一个事件的概率的基本方法是通过大量的重复试验; (3)概率是频率的稳定值,而频率是概率的近似值; (4)概率反映了随机事件发生的可能性的大小; (5)必然事件的概率为1,不可能事件的概率为0.因此 . (2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率;不可能事件必然事件事情发生的可能性越来越大事情发生的可能性越来越小例1:有人说,既然抛掷一枚硬币出现正面的为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种想法正确吗?
答:这种说法是错误的,抛掷一枚硬币出现正面的概率为0.5,它是大量试验得出的一种规律性结果,对具体的几次试验来讲不一定能体现出这种规律性,在连续抛掷一枚硬币两次的试验中,可能两次均正面向上,也可能两次均反面向上,也可能一次正面向上,一次反面向上例2:若某种彩票准备发行1000万张,其中有1万张可以中奖,则买一张这种彩票的中奖概率是多少?买1000张的话是否一定会中奖?答:不一定中奖,因为买彩票是随机的,每张彩票都可能中奖也可能不中奖。买彩票中奖的概率为1/1000,是指试验次数相当大,即随着购买彩票的张数的增加,大约有1/1000的彩票中奖。例3:在一场乒乓球比赛前,裁判员利用抽签器来决定由谁先发球,请用概率的知识解释其公平性。分析:这个规则是公平的,因为每个运动员先发球的概率为0.5,即每个运动员取得先发球权的概率是0.5。解:这个规则是公平的,因为抽签上抛后,红圈
朝上与绿圈朝上的概率均是0.5,因此任何一名运
动员猜中的概率都是0.5,也就是每个运动员取得
先发球权的概率都是0.5。00.51说明下列事件的概率,并标在图上请你来帮忙(1)(2)(3)(4) 掷一粒骰子,正面朝上的数字是 3 的倍数.(4)例1:对一批衬衫进行抽查,结果如下表:0.880.890.9010.905求抽取一件衬衫是优等品的概率约是多少?抽取衬衫2000件,约有优质品几件? 对某电视机厂生产的电视机进行抽样检测的数据如下: (1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少? 解:⑴ 各次优等品频率依次为 ⑵优等品的概率为:0.950.8,0.92,0.96,0.95,0.956,0.954请看下面两个试验:
1、从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,共有5种结果;
2、投一枚骰子,向上的一面的点数有6种; 一般地,如果在一次试验中,有n中可能的
结果,事件A包含其中的m种结果,那么事件A
发生的概率归纳例 :投掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)掷得点数为2
(2)掷得点数为奇数
(3)掷得的点数大于2且小于5;如图:是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率。(1)指向红色;(2) 指向红色或黄色;(3) 不指向红色。解:一共有7中等可能的结果。
(1)指向红色有3种结果,
P(红色)=_____
(2)指向红色或黄色一共有5种
等可能的结果,P( 红或黄)=_______
(3)不指向红色有4种等可能的结果
P( 不指红)= ________练习
(1) 抛掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1至6的点数,则掷得点数是2的概率是___.
(2) 袋中共有5个大小相同的红球、白球,任意摸出一球为红球的概率是 。如图,由A村去B村的道路有三条,由B村去C村的道路有两条(1)从A村经B村去C村有多少中不同走法?(2)某人从中任选一条路线,选中先经A---B中路,再经B---C南路的概率是多少?ABC北中南北南小华用电脑设计了一个小猫跳转的实验,如图所示,图形由黑白两种颜色的20块方砖组成,方砖的大小完全一样,小猫在方砖上可自由走动并随意停止。
(1)在这个实验中,小猫停留在黑砖上的概率是多少?
(2)要使小猫停留在黑砖上的概率是0.6,在不改变方砖数目的情况下,其他颜色应作怎样的调整?8÷20=0.4黑砖需 20×0.6=12 块甲、乙 两人做如下的游戏:你认为这个游戏
对甲、乙双方公平吗? 如图是一个均匀的骰子,它的每个面上分别标有数字1,2,3,4,5,6。
任意掷出骰子后,若朝上的数字是6,则甲获胜;若朝上的数字不是6,则乙获胜。小结1.随机事件的概念2.随机事件的概率的定义 在一定条件下可能发生也可能不发生的事件,叫做随机事件. 在大量重复进行同一试验时, 事件 发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率.(1) 甲自由转动转盘A,同时乙自由转动转盘B;(2) 转盘停止后,指针指向几就顺时针走几格,得到一个
数字 (如,在转盘A中, 如果指针指向3, 就按顺时针方向走3格,得到数字6);(3) 如果最终得到的数字是偶数就得1分,否则不得分;(4) 转动10次转盘,记录每次得分的结果,累计得分高的
人为胜者。 本图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形。利用这两个转盘做下面的游戏: 这个游戏对甲、乙双方公平吗?说说你的理由。123456135246AB甲得分的情况转盘A(1)如果指针指向奇数, 如“3”,则按顺时针方向走3格,得到数字6,所得数字是偶数,得1分; 同理, 当第一次指针指向其它的奇数 a 时,
指针顺时针方向转动同样的格数 a,
所得结果数应是 2a 或(2a–6)(a≥3),
即所得结果数总是偶数. 如6, 指针顺时针方向转动同样的格数 b,
故所得结果数应是 2b 或(2b–6)(b≥4),
所得结果数也是偶数. 总之, 甲每次所得结果数总是偶数. 乙得分的情况转盘B(1)如果指针指向奇数, 如“3”,则按顺时针方向走3格,得到数字4,所得到的数字是偶数,得1分;如4, 指针顺时针方向转动4格, 得到数字5,所得到数字是奇数,不得分; 因此, 乙每次所得到的数字可能是奇数,也可能是偶数; 每次得分与不得分不能确定. 而甲每次指针转动后所得到的数字总是偶数,因此, 本转盘游戏对乙不公平. (1)对于转盘A,
“最终得到的数字是偶数”这个事件转盘A是必然的、不可能的还是不确定的? 是必然的“最终得到的数字是奇数”呢?是不可能的;“最终得到的数字是偶数”这个事件是必然的、不可能的还是不确定的? 是不确定的;“最终得到的数字是奇数”呢?是不确定的;(3)你能用自己的语言描述必然事件发生的可能性吗?
概率论产生于十七世纪,本来是由保险事业的发展而产生的,但是来自于赌博者的请求,却是数学家们思考概率论问题的源泉。
传说早在1654年,有一个赌徒梅累向当时的数学家帕斯卡提出一个使他苦恼了很久的问题:“两个赌徒相约赌若干局,谁先赢 3局就算赢,全部赌本就归谁。但是当其中一个人赢了 2局,另一个人赢了1局的时候,由于某种原因,赌博终止了。问:赌本应该如何分法才合理?”
帕斯卡是17世纪著名的数学家,但这个问题却让他苦苦思索了三年,三年后,也就是1657年,荷兰著名的数学家惠更斯企图自己解决这一问题,结果写成了《论赌博中的计算》一书,这就是概率论最早的一部著作。
近几十年来,随着科技的蓬勃发展,概率论大量应用到国民经济、工农业生产及各学科领域。许多兴起的应用数学,如信息论、对策论、排队论、控制论等,都是以概率论作为基础的。
指出下列事件中,哪些是不可能事件?哪些是必然事件?哪些是随机事件?(2)手电筒的电池没电,灯泡发亮.(5)当 x 是实数时,x2 ≥ 0; (6)一个袋内装有形状大小相同的一个白球和一个黑球,从中任意摸出1个球则为白球. (3)在标准大气压下,水在温度 时沸腾;(4)直线 过定点 ;(1)某地1月1日刮西北风;(7)、打开电视机,正在播广告;
(8)、我区每年都会下雨;
(9)、明天的太阳从西方升起来;
(10)、掷两个骰子两个6朝上;
(11)、异号两数相乘,积为正数;
(12)、某种电器工作时,机身发热;探究:投掷硬币时,国徽朝上的可能性有多大?在同样条件下,随机事件可能发生,也可能不发生,那么它发生的可能性有多大呢?这是我们下面要讨论的问题。历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示实验结论:当抛硬币的次数很多时,出现下面的频率值是
稳定的,接近于常数0.5,在它附近摆动. 随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
生呈现出一定的规律性.出现的频率值接近于常数.随机事件及其概率某批乒乓球产品质量检查结果表: 当抽查的球数很多时,抽到优等品的频率 接近于常数0.95,在它附近摆动。 很多常数某种油菜籽在相同条件下的发芽试验结果表: 当试验的油菜籽的粒数很多时,油菜籽发芽
的频率 接近于常数0.9,在它附近摆动。很多 常数随机事件及其概率事件 的概率的定义: 一般地,在大量重复进行同一试验时,事件 发生的频率 (n为实验的次数,m是事件发生的频数)总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率,记做 . 事件一般用大写英文字母A,B,C,...表示 事件发生的可能性越大,则它的概率越接近1;事件发生的可能性越小,则它的概率越接近0.由定义可知: (1)求一个事件的概率的基本方法是通过大量的重复试验; (3)概率是频率的稳定值,而频率是概率的近似值; (4)概率反映了随机事件发生的可能性的大小; (5)必然事件的概率为1,不可能事件的概率为0.因此 . (2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率;不可能事件必然事件事情发生的可能性越来越大事情发生的可能性越来越小例1:有人说,既然抛掷一枚硬币出现正面的为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种想法正确吗?
答:这种说法是错误的,抛掷一枚硬币出现正面的概率为0.5,它是大量试验得出的一种规律性结果,对具体的几次试验来讲不一定能体现出这种规律性,在连续抛掷一枚硬币两次的试验中,可能两次均正面向上,也可能两次均反面向上,也可能一次正面向上,一次反面向上例2:若某种彩票准备发行1000万张,其中有1万张可以中奖,则买一张这种彩票的中奖概率是多少?买1000张的话是否一定会中奖?答:不一定中奖,因为买彩票是随机的,每张彩票都可能中奖也可能不中奖。买彩票中奖的概率为1/1000,是指试验次数相当大,即随着购买彩票的张数的增加,大约有1/1000的彩票中奖。例3:在一场乒乓球比赛前,裁判员利用抽签器来决定由谁先发球,请用概率的知识解释其公平性。分析:这个规则是公平的,因为每个运动员先发球的概率为0.5,即每个运动员取得先发球权的概率是0.5。解:这个规则是公平的,因为抽签上抛后,红圈
朝上与绿圈朝上的概率均是0.5,因此任何一名运
动员猜中的概率都是0.5,也就是每个运动员取得
先发球权的概率都是0.5。00.51说明下列事件的概率,并标在图上请你来帮忙(1)(2)(3)(4) 掷一粒骰子,正面朝上的数字是 3 的倍数.(4)例1:对一批衬衫进行抽查,结果如下表:0.880.890.9010.905求抽取一件衬衫是优等品的概率约是多少?抽取衬衫2000件,约有优质品几件? 对某电视机厂生产的电视机进行抽样检测的数据如下: (1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率是多少? 解:⑴ 各次优等品频率依次为 ⑵优等品的概率为:0.950.8,0.92,0.96,0.95,0.956,0.954请看下面两个试验:
1、从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,共有5种结果;
2、投一枚骰子,向上的一面的点数有6种; 一般地,如果在一次试验中,有n中可能的
结果,事件A包含其中的m种结果,那么事件A
发生的概率归纳例 :投掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)掷得点数为2
(2)掷得点数为奇数
(3)掷得的点数大于2且小于5;如图:是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率。(1)指向红色;(2) 指向红色或黄色;(3) 不指向红色。解:一共有7中等可能的结果。
(1)指向红色有3种结果,
P(红色)=_____
(2)指向红色或黄色一共有5种
等可能的结果,P( 红或黄)=_______
(3)不指向红色有4种等可能的结果
P( 不指红)= ________练习
(1) 抛掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1至6的点数,则掷得点数是2的概率是___.
(2) 袋中共有5个大小相同的红球、白球,任意摸出一球为红球的概率是 。如图,由A村去B村的道路有三条,由B村去C村的道路有两条(1)从A村经B村去C村有多少中不同走法?(2)某人从中任选一条路线,选中先经A---B中路,再经B---C南路的概率是多少?ABC北中南北南小华用电脑设计了一个小猫跳转的实验,如图所示,图形由黑白两种颜色的20块方砖组成,方砖的大小完全一样,小猫在方砖上可自由走动并随意停止。
(1)在这个实验中,小猫停留在黑砖上的概率是多少?
(2)要使小猫停留在黑砖上的概率是0.6,在不改变方砖数目的情况下,其他颜色应作怎样的调整?8÷20=0.4黑砖需 20×0.6=12 块甲、乙 两人做如下的游戏:你认为这个游戏
对甲、乙双方公平吗? 如图是一个均匀的骰子,它的每个面上分别标有数字1,2,3,4,5,6。
任意掷出骰子后,若朝上的数字是6,则甲获胜;若朝上的数字不是6,则乙获胜。小结1.随机事件的概念2.随机事件的概率的定义 在一定条件下可能发生也可能不发生的事件,叫做随机事件. 在大量重复进行同一试验时, 事件 发生的频率 总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件 的概率.(1) 甲自由转动转盘A,同时乙自由转动转盘B;(2) 转盘停止后,指针指向几就顺时针走几格,得到一个
数字 (如,在转盘A中, 如果指针指向3, 就按顺时针方向走3格,得到数字6);(3) 如果最终得到的数字是偶数就得1分,否则不得分;(4) 转动10次转盘,记录每次得分的结果,累计得分高的
人为胜者。 本图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形。利用这两个转盘做下面的游戏: 这个游戏对甲、乙双方公平吗?说说你的理由。123456135246AB甲得分的情况转盘A(1)如果指针指向奇数, 如“3”,则按顺时针方向走3格,得到数字6,所得数字是偶数,得1分; 同理, 当第一次指针指向其它的奇数 a 时,
指针顺时针方向转动同样的格数 a,
所得结果数应是 2a 或(2a–6)(a≥3),
即所得结果数总是偶数. 如6, 指针顺时针方向转动同样的格数 b,
故所得结果数应是 2b 或(2b–6)(b≥4),
所得结果数也是偶数. 总之, 甲每次所得结果数总是偶数. 乙得分的情况转盘B(1)如果指针指向奇数, 如“3”,则按顺时针方向走3格,得到数字4,所得到的数字是偶数,得1分;如4, 指针顺时针方向转动4格, 得到数字5,所得到数字是奇数,不得分; 因此, 乙每次所得到的数字可能是奇数,也可能是偶数; 每次得分与不得分不能确定. 而甲每次指针转动后所得到的数字总是偶数,因此, 本转盘游戏对乙不公平. (1)对于转盘A,
“最终得到的数字是偶数”这个事件转盘A是必然的、不可能的还是不确定的? 是必然的“最终得到的数字是奇数”呢?是不可能的;“最终得到的数字是偶数”这个事件是必然的、不可能的还是不确定的? 是不确定的;“最终得到的数字是奇数”呢?是不确定的;(3)你能用自己的语言描述必然事件发生的可能性吗?
同课章节目录
