列举法习题课
图片预览






文档简介
课件20张PPT。列举法习题课问题:1.掷一个骰子,向上的一面数字是5的概率是___ .2.袋子中有2个红球,3个绿球,它们只有颜色上的区别,从袋子中随机地取出1个球是红球的概率是 __. 3.随机地掷两枚硬币,则两枚硬币全部正面朝上的概率是__.等可能事件概率复习等可能性事件的两种特征:
1.出现的结果有限多个;
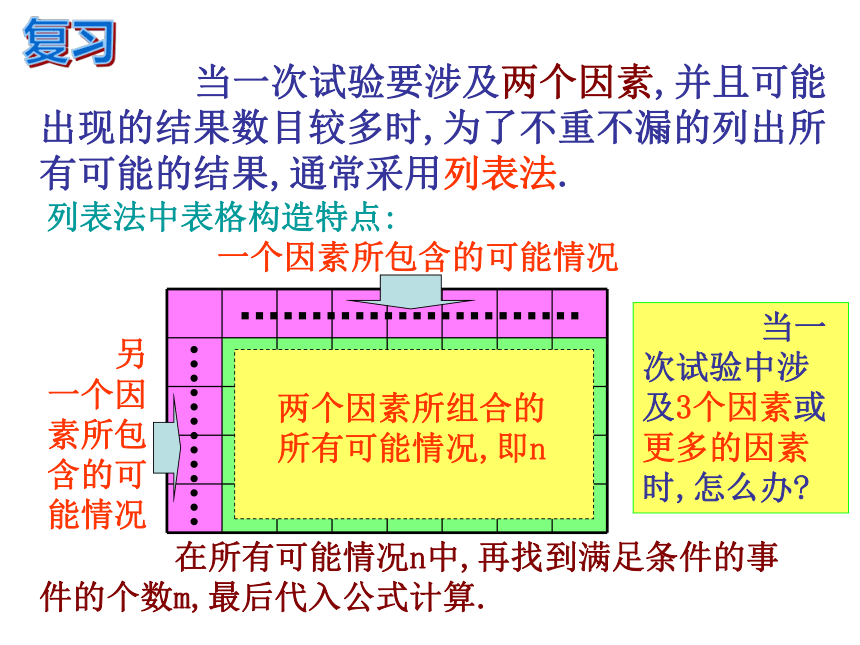
2.各结果发生的可能性相等;复习 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.一个因素所包含的可能情况 另一个因素所包含的可能情况两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.列表法中表格构造特点: 当一次试验中涉及3个因素或更多的因素时,怎么办? 若三人一起玩,每次用一只手同时随机出石头、剪
刀、布三种手势之一,则三人出相同手势的概率是______.
小明、小亮两人要去某风景区游玩,每天某一时刻开往该风景区有三辆票价相同,而舒适程度分为上、中、下三等的汽车 。 旅游中的概率(1)三辆车按出现的先后顺序共有哪几种不同的可能?解:(1)三辆车开过来的先后顺序有6种可能:
(上、中、下)、(上、下、中)、 (中、上、下)、
(中、下、上)、(下、上、中)、 (下、中、上)。(2)两人采用了不同的乘车方案:
小明的方案:无论如何总是上开来的第一辆车。 你认为哪一种方案乘坐上等车的可能性大?为什么?
小亮的方案:不上开过来的第一辆车,而是仔细观察车的舒适状
况,如果第二辆车的状况比第一辆好,他就上第二辆;如果第二
辆不比第一辆好,他就上第三辆车。
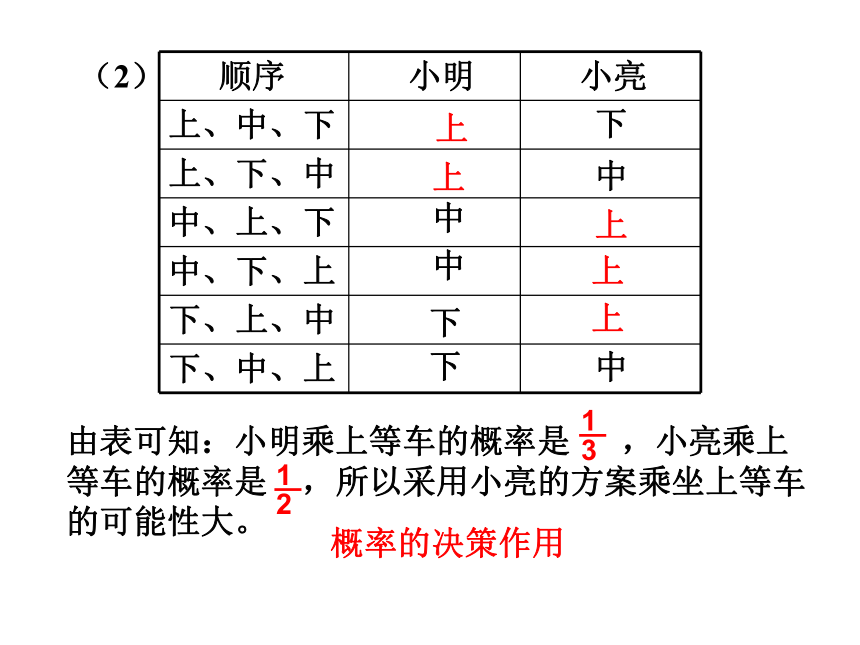
(2)由表可知:小明乘上等车的概率是 ,小亮乘上等车的概率是 ,所以采用小亮的方案乘坐上等车的可能性大。概率的决策作用 上下上中中上上上中中下下1.一个家庭有三个孩子,若一个孩子是男孩还是女孩的可能性相同.
(1)求这个家庭的3个孩子都是男孩的概率;
(2)求这个家庭有2个男孩和1个女孩的概率;
(3)求这个家庭至少有一个男孩的概率.例题某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图9所示),并规定:顾客每购买100元的商品,可转动两次转盘,当转盘停止后,看指针指向的数。获奖方法是:①指针两次都指向8时,顾客可以获得100元购物券;②指针两次中有一次指向8时,顾客可以获得50元购物券;③指针两次都不指向8,且所指两数之和又大于8时,顾客可以获得所指两数之和与8的差的10倍的购物券(如6+6-8=4,获40元购物券);④其余情况无奖,若顾客不愿意转动转盘,可以直接获得25元购物券。
(1)试用树状图或列表的方法,给出两次转动转盘指针所有可能指向的结果;
(2)试求顾客可获得100元购物券的概率;
(3)试求顾客无奖的概率。
(4)你认为转动转盘和直接获得购
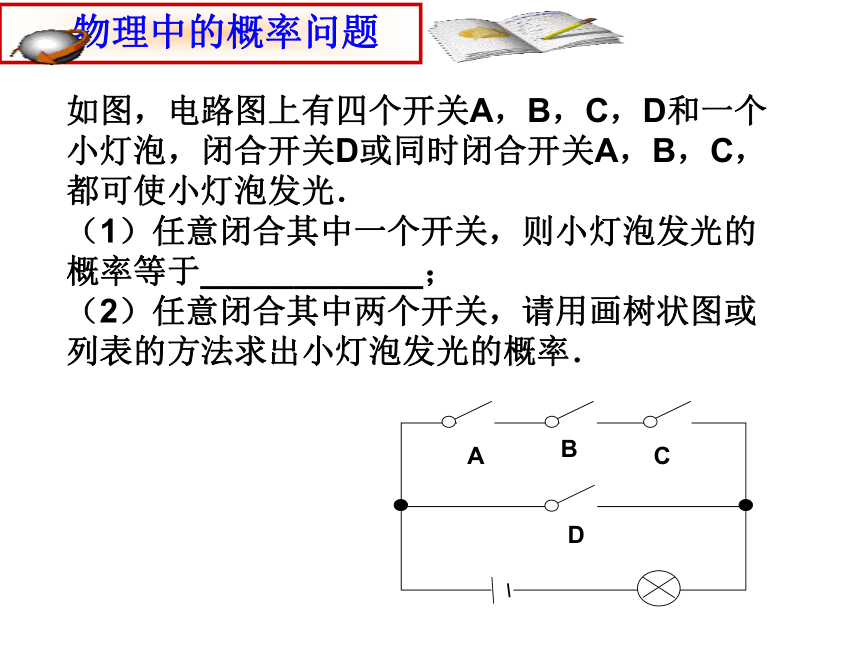
物券哪种方式对顾客更合算?试说明理由。如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C,都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于____________;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.ADBC右图是由转盘和箭头组成的两个装置,装置A,B的转盘分别被分成三个面积相等的扇形,装置A上的数字分别是1,6,8,装置B上的数字分别是4,5,7,这两个装置除了表面数字不同外,其他构造完全相同.现在你和另外一个人分别同时用力转动A,B两个转盘,如果我们规定箭头停留在较大数字的一方获胜(若箭头恰好停留在分界线上,则重新转动一次,直到箭头停留在某一数字为止),那么,你会选择哪个装置呢?请借助列表法(或树状图)说说理由.AB861574根据生物学家的研究,人体的许多特征都是由基因控制的,有的人是单眼皮,有的人是双眼皮,这是由一对人体基因控制的,控制单眼皮的基因f是隐性的,控制双眼皮的基因F是显性的,这样控制眼皮的一对基因可能是ff、FF或Ff,基因ff的人是单眼皮,基因FF或Ff的人是双眼皮.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的,例如,父母都是双眼皮而且他们的基因都是Ff,那么他们的子女只有ff、FF或Ff三种可能,具体可用下表表示:
你能计算出他们的子女是双眼皮的概率吗?如果父亲的基因是ff,母亲的基因是FF呢?如果父亲的基因是Ff,母亲的基因是ff呢?经过某十字路口的汽车,它可能继续直行,
也可能向左转或向右转,如果这三种可能性
大小相同。三辆汽车经过这个十字路口,求
下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左传。经过某十字路口的汽车,它可能继续直行,也可能左转或右转,如果这三种可能性大小相同,同向而行的三辆汽车都经过这个十字路口时,求下列事件的概率:(1)三辆车全部继续直行(2)两辆车右转,一辆车左转(3)至少有两辆车左转 解:由树形图得,所有可能出现的结果有27个,它们出现的可能性相等。
(1)三辆车全部继续直行的结果有1个,则 P(三辆车全部继续直行)=
(2)两辆车右转,一辆车左转的结果有3个,则
P(两辆车右转,一辆车左转)= =
(3)至少有两辆车左转的结果有7个,则 P(至少有两辆车左转)=1、两道单项选择题都含有A、B、C、D四个选项,若某学生不知道正确答案就瞎猜,则这两道题恰好全部被猜对的概率是( )
A B C D
2、如图,小明的奶奶家到学校有3条路可走,学校到小明的外婆家也有3条路可走,若小明要从奶奶家经学校到外婆家,不同的走法共有________种
3、某校八年级将举行班级乒乓球对抗赛,每个班必须选派出一对男女混合双打选手参赛,八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中,选男、女选手各一名组成一对参赛组合,一共能够组成哪几对?如果小敏和小强的组合是最强组合,那么采用随机抽签的办法,恰好选出小敏和小强参赛的概率是多少?116用列举法求概率甲、乙两同学各拿一枚完全相同的硬币进行投掷实验,规定国徽为正面。两人同时掷出硬币为一次实验,在进行200次实验后,他们将向上一面的结果汇总如下表:
(1)根据表格提供的信息分别求出事件A、 B、C发生的频率;
(2)分别求出事件A、B、C发生的理论概率;(3)比较同一事件的频率与概率是否一致?答:(1)事件A发生的频率为:
事件B发生的频率为:
事件C发生的频率为:
(2)树状图可以是: ∴事件A、B、C发生的理论概率分别为: P(A)=1/4=0.25,P(B)=2/4=0.5,
P(C)= 1/4=0.25.
(3)经过200次实验后事件B发生的频率
与理论概率是一致的,事件A、C发生的频率
与理论概率略有误差。是真是假 从一定高度随机掷一枚均匀的硬币,落地后其朝上的一面可能出现正面和反面这样两种等可能的结果.小明正在做掷硬币的试验,他已经掷了3次硬币,不巧的是这3次都是正面朝上.那么,你认为小明第4次掷硬币,出现正面朝上的可能性大,还是反面朝上的可能性大,还是一样大?说说你的理由,并与同伴进行交流. 第4次掷硬币,出现正面朝上的可能性与反面朝上的可能性一样大.把4个不同的球任意投入4个不同的盒子内(每盒装球不限),计算:
(1)无空盒的概率;
(2)恰有一个空盒的概率。把3个不同的球任意投入3个不同的盒子内(每盒装球不限),计算: (1)无空盒的概率; (2)恰有一个空盒的概率.解: 由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.∴ P(无空盒)=(1)无空盒的结果有6个(2)恰有一个空盒的结果有18个∴ P(恰有一个空盒)=
1.出现的结果有限多个;
2.各结果发生的可能性相等;复习 当一次试验要涉及两个因素,并且可能出现的结果数目较多时,为了不重不漏的列出所有可能的结果,通常采用列表法.一个因素所包含的可能情况 另一个因素所包含的可能情况两个因素所组合的所有可能情况,即n 在所有可能情况n中,再找到满足条件的事件的个数m,最后代入公式计算.列表法中表格构造特点: 当一次试验中涉及3个因素或更多的因素时,怎么办? 若三人一起玩,每次用一只手同时随机出石头、剪
刀、布三种手势之一,则三人出相同手势的概率是______.
小明、小亮两人要去某风景区游玩,每天某一时刻开往该风景区有三辆票价相同,而舒适程度分为上、中、下三等的汽车 。 旅游中的概率(1)三辆车按出现的先后顺序共有哪几种不同的可能?解:(1)三辆车开过来的先后顺序有6种可能:
(上、中、下)、(上、下、中)、 (中、上、下)、
(中、下、上)、(下、上、中)、 (下、中、上)。(2)两人采用了不同的乘车方案:
小明的方案:无论如何总是上开来的第一辆车。 你认为哪一种方案乘坐上等车的可能性大?为什么?
小亮的方案:不上开过来的第一辆车,而是仔细观察车的舒适状
况,如果第二辆车的状况比第一辆好,他就上第二辆;如果第二
辆不比第一辆好,他就上第三辆车。
(2)由表可知:小明乘上等车的概率是 ,小亮乘上等车的概率是 ,所以采用小亮的方案乘坐上等车的可能性大。概率的决策作用 上下上中中上上上中中下下1.一个家庭有三个孩子,若一个孩子是男孩还是女孩的可能性相同.
(1)求这个家庭的3个孩子都是男孩的概率;
(2)求这个家庭有2个男孩和1个女孩的概率;
(3)求这个家庭至少有一个男孩的概率.例题某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图9所示),并规定:顾客每购买100元的商品,可转动两次转盘,当转盘停止后,看指针指向的数。获奖方法是:①指针两次都指向8时,顾客可以获得100元购物券;②指针两次中有一次指向8时,顾客可以获得50元购物券;③指针两次都不指向8,且所指两数之和又大于8时,顾客可以获得所指两数之和与8的差的10倍的购物券(如6+6-8=4,获40元购物券);④其余情况无奖,若顾客不愿意转动转盘,可以直接获得25元购物券。
(1)试用树状图或列表的方法,给出两次转动转盘指针所有可能指向的结果;
(2)试求顾客可获得100元购物券的概率;
(3)试求顾客无奖的概率。
(4)你认为转动转盘和直接获得购
物券哪种方式对顾客更合算?试说明理由。如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C,都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于____________;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.ADBC右图是由转盘和箭头组成的两个装置,装置A,B的转盘分别被分成三个面积相等的扇形,装置A上的数字分别是1,6,8,装置B上的数字分别是4,5,7,这两个装置除了表面数字不同外,其他构造完全相同.现在你和另外一个人分别同时用力转动A,B两个转盘,如果我们规定箭头停留在较大数字的一方获胜(若箭头恰好停留在分界线上,则重新转动一次,直到箭头停留在某一数字为止),那么,你会选择哪个装置呢?请借助列表法(或树状图)说说理由.AB861574根据生物学家的研究,人体的许多特征都是由基因控制的,有的人是单眼皮,有的人是双眼皮,这是由一对人体基因控制的,控制单眼皮的基因f是隐性的,控制双眼皮的基因F是显性的,这样控制眼皮的一对基因可能是ff、FF或Ff,基因ff的人是单眼皮,基因FF或Ff的人是双眼皮.在遗传时,父母分别将他们所携带的一对基因中的一个遗传给子女,而且是等可能的,例如,父母都是双眼皮而且他们的基因都是Ff,那么他们的子女只有ff、FF或Ff三种可能,具体可用下表表示:
你能计算出他们的子女是双眼皮的概率吗?如果父亲的基因是ff,母亲的基因是FF呢?如果父亲的基因是Ff,母亲的基因是ff呢?经过某十字路口的汽车,它可能继续直行,
也可能向左转或向右转,如果这三种可能性
大小相同。三辆汽车经过这个十字路口,求
下列事件的概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左传。经过某十字路口的汽车,它可能继续直行,也可能左转或右转,如果这三种可能性大小相同,同向而行的三辆汽车都经过这个十字路口时,求下列事件的概率:(1)三辆车全部继续直行(2)两辆车右转,一辆车左转(3)至少有两辆车左转 解:由树形图得,所有可能出现的结果有27个,它们出现的可能性相等。
(1)三辆车全部继续直行的结果有1个,则 P(三辆车全部继续直行)=
(2)两辆车右转,一辆车左转的结果有3个,则
P(两辆车右转,一辆车左转)= =
(3)至少有两辆车左转的结果有7个,则 P(至少有两辆车左转)=1、两道单项选择题都含有A、B、C、D四个选项,若某学生不知道正确答案就瞎猜,则这两道题恰好全部被猜对的概率是( )
A B C D
2、如图,小明的奶奶家到学校有3条路可走,学校到小明的外婆家也有3条路可走,若小明要从奶奶家经学校到外婆家,不同的走法共有________种
3、某校八年级将举行班级乒乓球对抗赛,每个班必须选派出一对男女混合双打选手参赛,八年级一班准备在小娟、小敏、小华三名女选手和小明、小强两名男选手中,选男、女选手各一名组成一对参赛组合,一共能够组成哪几对?如果小敏和小强的组合是最强组合,那么采用随机抽签的办法,恰好选出小敏和小强参赛的概率是多少?116用列举法求概率甲、乙两同学各拿一枚完全相同的硬币进行投掷实验,规定国徽为正面。两人同时掷出硬币为一次实验,在进行200次实验后,他们将向上一面的结果汇总如下表:
(1)根据表格提供的信息分别求出事件A、 B、C发生的频率;
(2)分别求出事件A、B、C发生的理论概率;(3)比较同一事件的频率与概率是否一致?答:(1)事件A发生的频率为:
事件B发生的频率为:
事件C发生的频率为:
(2)树状图可以是: ∴事件A、B、C发生的理论概率分别为: P(A)=1/4=0.25,P(B)=2/4=0.5,
P(C)= 1/4=0.25.
(3)经过200次实验后事件B发生的频率
与理论概率是一致的,事件A、C发生的频率
与理论概率略有误差。是真是假 从一定高度随机掷一枚均匀的硬币,落地后其朝上的一面可能出现正面和反面这样两种等可能的结果.小明正在做掷硬币的试验,他已经掷了3次硬币,不巧的是这3次都是正面朝上.那么,你认为小明第4次掷硬币,出现正面朝上的可能性大,还是反面朝上的可能性大,还是一样大?说说你的理由,并与同伴进行交流. 第4次掷硬币,出现正面朝上的可能性与反面朝上的可能性一样大.把4个不同的球任意投入4个不同的盒子内(每盒装球不限),计算:
(1)无空盒的概率;
(2)恰有一个空盒的概率。把3个不同的球任意投入3个不同的盒子内(每盒装球不限),计算: (1)无空盒的概率; (2)恰有一个空盒的概率.解: 由树形图可以看出,所有可能的结果有27种,它们出现的可能性相等.∴ P(无空盒)=(1)无空盒的结果有6个(2)恰有一个空盒的结果有18个∴ P(恰有一个空盒)=
同课章节目录
