27.2.1相似三角形的判定3
文档属性
| 名称 | 27.2.1相似三角形的判定3 |

|
|
| 格式 | rar | ||
| 文件大小 | 470.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-12-28 00:00:00 | ||
图片预览


文档简介
课件18张PPT。27.2.1 相似三角形的判定(第3课时)义务教育课程标准实验教科书九年级 上册人民教育出版社(2)∵DE∥BC
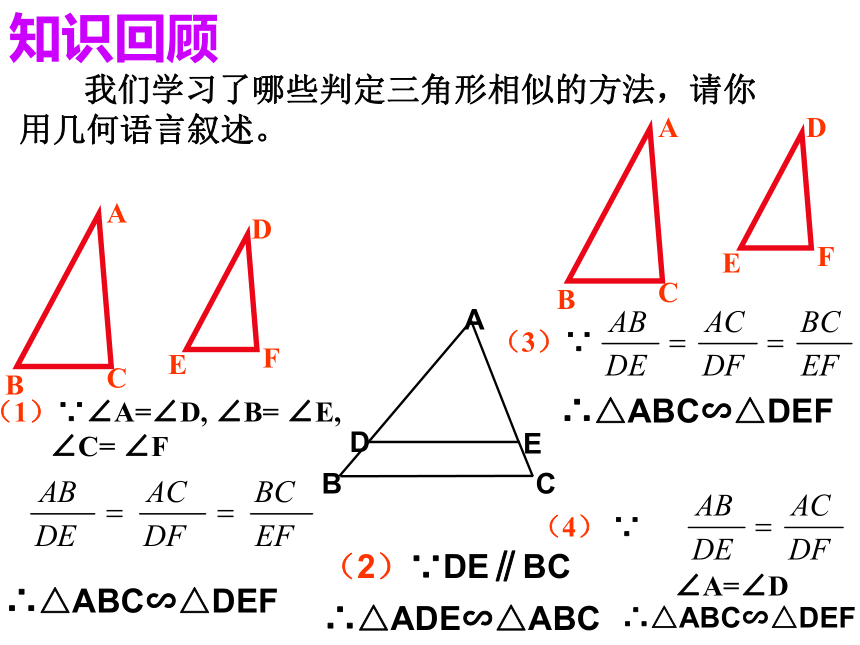
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用几何语言叙述。知识回顾(1)∵∠A=∠D, ∠B= ∠E,
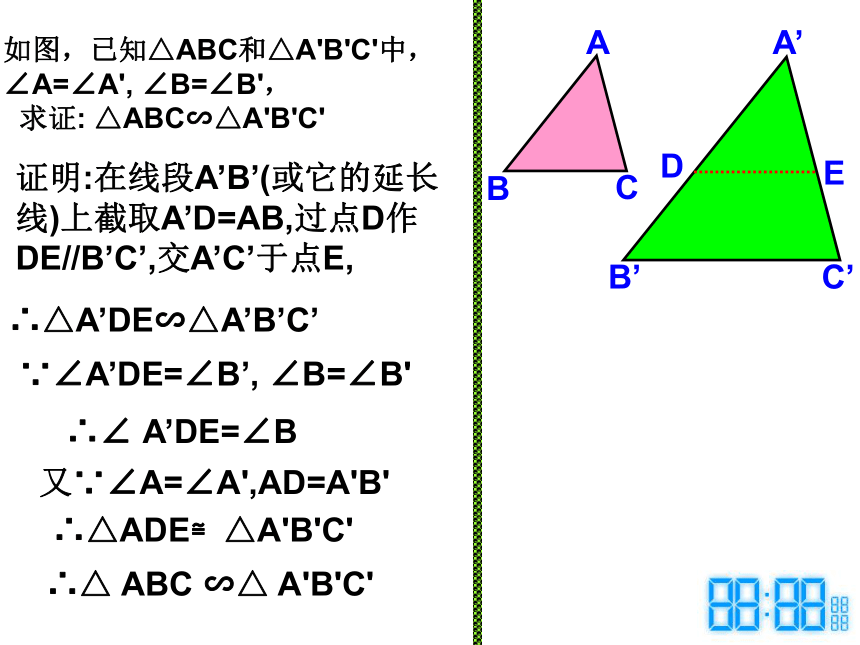
∠C= ∠F∴△ABC∽△DEF(3)∵∴△ABC∽△DEF(4) ∵∠A=∠D∴△ABC∽△DEF问题引入: 观察两副三角尺,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的。一般地,如果两个三角形有两组对应角相等,它们一定相似吗?探究:作△ABC 和△DEF,使得∠A=∠D, ∠B= ∠E,这时它们的第三个角满足∠C= ∠F吗?分别度量这两个三角形的边长,计算 ,你有什么发现?△ABC 和△DEF相似吗?猜想:请你证明:如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
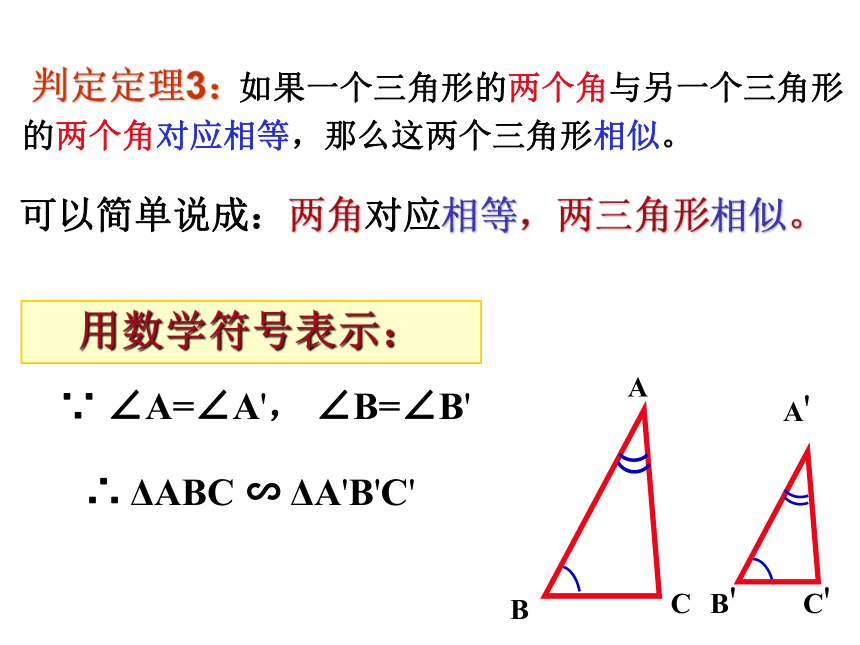
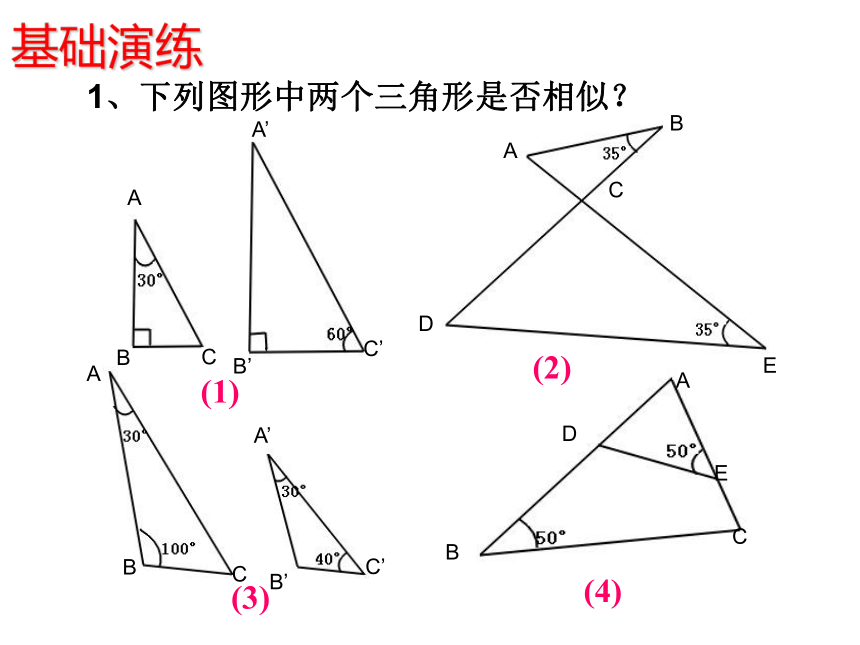
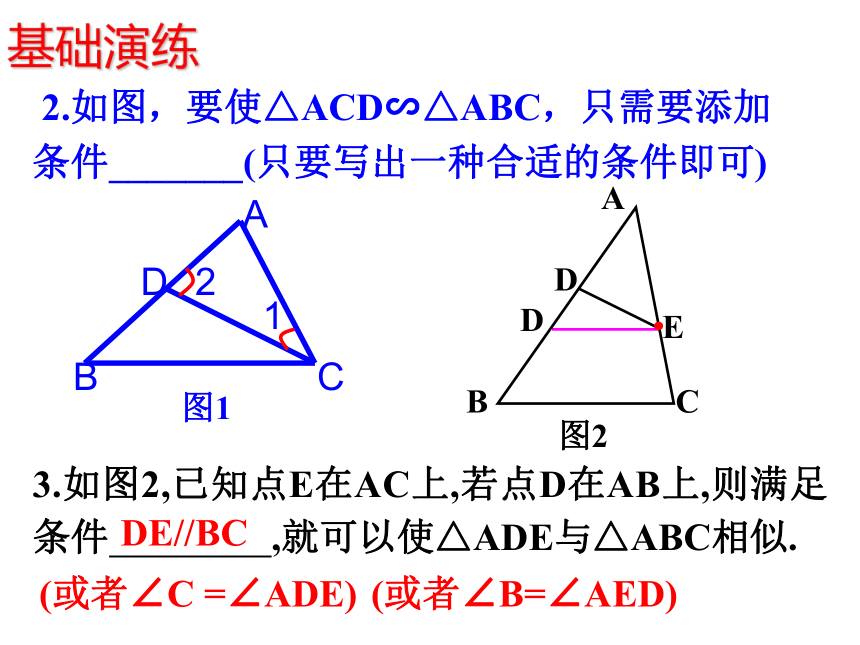
求证: △ABC∽△A'B'C'证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,DE∴△A’DE∽△A’B’C’∵∠A’DE=∠B’, ∠B=∠B'∴∠ A’DE=∠B又∵∠A=∠A',AD=A'B'∴△ADE≌△A'B'C'∴△ ABC ∽△ A'B'C'CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示: 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。判定定理3:基础演练1、下列图形中两个三角形是否相似?(1)(2)(3)(4) 2.如图,要使△ACD∽△ABC,只需要添加条件_______(只要写出一种合适的条件即可)3.如图2,已知点E在AC上,若点D在AB上,则满足条件 ,就可以使△ADE与△ABC相似.DD图1DE//BC(或者∠C =∠ADE)(或者∠B=∠AED)基础演练3、判断题:
⑴ 所有的直角三角形都相似 . ( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×√√×基础演练如图,弦AB和CD相交于⊙O内一点P,
求证:PA ? PB = PC?PD例题1引申1:如果弦AB和CD相交于圆O外一点P,结论还成立吗?引申2:上题中A,B重合为一点时,又会有什么结论?1.已知如图直线BE、DC交于A , ∠E= ∠C
求证:DA·AC=AB·AEDEABC证明:
∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AE练习2.如图,AD是△ABC的高,AE是△ABC的外接圆的直径,求证:AB·AC=AE·AD。辅助线1辅助线2分析:要证:AB·AC=AE·AD证:△ABE与△ADC相似证:△ABD与△ACE相似练习例2、求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:求证(2)AC2=AD · AB CD2=AD · DB
如图:在Rt △ ABC中, ∠ACB=900,CD⊥AB于D,
若 AC=6 ,AD=2,求AB,CD,BC的长相似三角形的识别方法有那些?方法1:通过定义方法5:两角对应相等。课 堂 小 结方法2:预备定理。方法3:三边对应成比例。方法4:两边对应成比例且夹角相等。 如图,在Rt△ABC的一边AC上有一点P(点P与点A, C不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?ABCP· 常见
图形练习.如图直线BE、DC交于A, AD·AC=AE·BA,
求证:∠E=∠C如何证明∠DEA=∠C?
EABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =43.已知如图, ∠ABD=∠C AD=2 , AC=8,求AB
∴△ADE∽△ABC 我们学习了哪些判定三角形相似的方法,请你用几何语言叙述。知识回顾(1)∵∠A=∠D, ∠B= ∠E,
∠C= ∠F∴△ABC∽△DEF(3)∵∴△ABC∽△DEF(4) ∵∠A=∠D∴△ABC∽△DEF问题引入: 观察两副三角尺,其中同样角度(30°与60°,或45°与45°)的两个三角尺大小可能不同,但它们看起来是相似的。一般地,如果两个三角形有两组对应角相等,它们一定相似吗?探究:作△ABC 和△DEF,使得∠A=∠D, ∠B= ∠E,这时它们的第三个角满足∠C= ∠F吗?分别度量这两个三角形的边长,计算 ,你有什么发现?△ABC 和△DEF相似吗?猜想:请你证明:如图,已知△ABC和△A'B'C'中,∠A=∠A', ∠B=∠B',
求证: △ABC∽△A'B'C'证明:在线段A’B’(或它的延长线)上截取A’D=AB,过点D作DE//B’C’,交A’C’于点E,DE∴△A’DE∽△A’B’C’∵∠A’DE=∠B’, ∠B=∠B'∴∠ A’DE=∠B又∵∠A=∠A',AD=A'B'∴△ADE≌△A'B'C'∴△ ABC ∽△ A'B'C'CC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示: 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。判定定理3:基础演练1、下列图形中两个三角形是否相似?(1)(2)(3)(4) 2.如图,要使△ACD∽△ABC,只需要添加条件_______(只要写出一种合适的条件即可)3.如图2,已知点E在AC上,若点D在AB上,则满足条件 ,就可以使△ADE与△ABC相似.DD图1DE//BC(或者∠C =∠ADE)(或者∠B=∠AED)基础演练3、判断题:
⑴ 所有的直角三角形都相似 . ( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×√√×基础演练如图,弦AB和CD相交于⊙O内一点P,
求证:PA ? PB = PC?PD例题1引申1:如果弦AB和CD相交于圆O外一点P,结论还成立吗?引申2:上题中A,B重合为一点时,又会有什么结论?1.已知如图直线BE、DC交于A , ∠E= ∠C
求证:DA·AC=AB·AEDEABC证明:
∵ ∠E=∠C ∠DAE=∠BAC
∴ △ABC ∽ △ADE
∴ AC :AE=AB :AD
∴ DA · AC=AB · AE练习2.如图,AD是△ABC的高,AE是△ABC的外接圆的直径,求证:AB·AC=AE·AD。辅助线1辅助线2分析:要证:AB·AC=AE·AD证:△ABE与△ADC相似证:△ABD与△ACE相似练习例2、求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:求证(2)AC2=AD · AB CD2=AD · DB
如图:在Rt △ ABC中, ∠ACB=900,CD⊥AB于D,
若 AC=6 ,AD=2,求AB,CD,BC的长相似三角形的识别方法有那些?方法1:通过定义方法5:两角对应相等。课 堂 小 结方法2:预备定理。方法3:三边对应成比例。方法4:两边对应成比例且夹角相等。 如图,在Rt△ABC的一边AC上有一点P(点P与点A, C不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条?ABCP· 常见
图形练习.如图直线BE、DC交于A, AD·AC=AE·BA,
求证:∠E=∠C如何证明∠DEA=∠C?
EABDC解: ∵ ∠ A= ∠ A ∠ABD=∠C
∴ △ABD ∽ △ACB
∴ AB : AC=AD : AB
∴ AB2 = AD · AC
∵ AD=2 AC=8
∴ AB =43.已知如图, ∠ABD=∠C AD=2 , AC=8,求AB
