锐角三角函数(1)
图片预览



文档简介
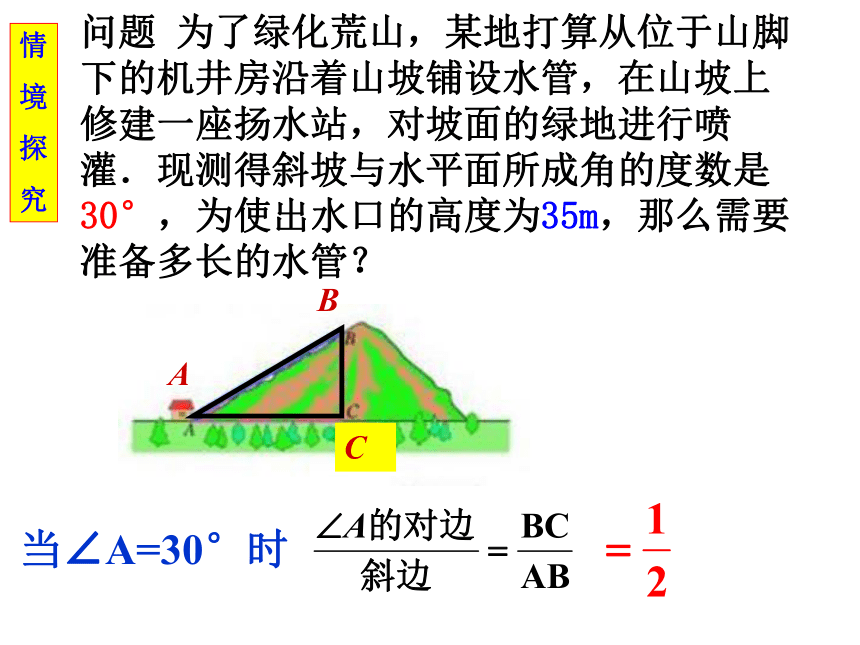
课件23张PPT。28.1 锐角三角函数(1)义务教育课程标准实验教科书九年级 上册人民教育出版社问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
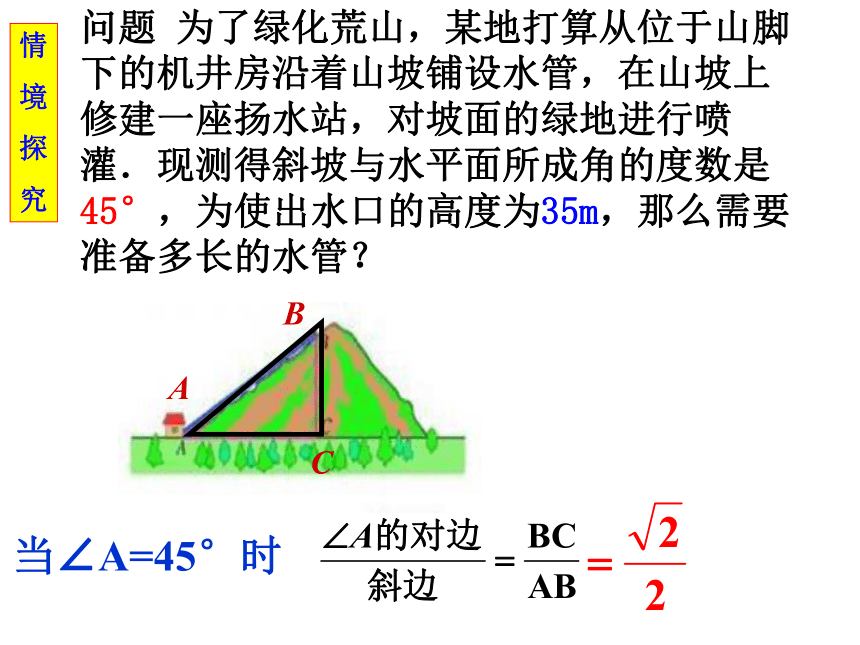
究当∠A=30°时问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是45°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
究当∠A=45°时问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是60°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
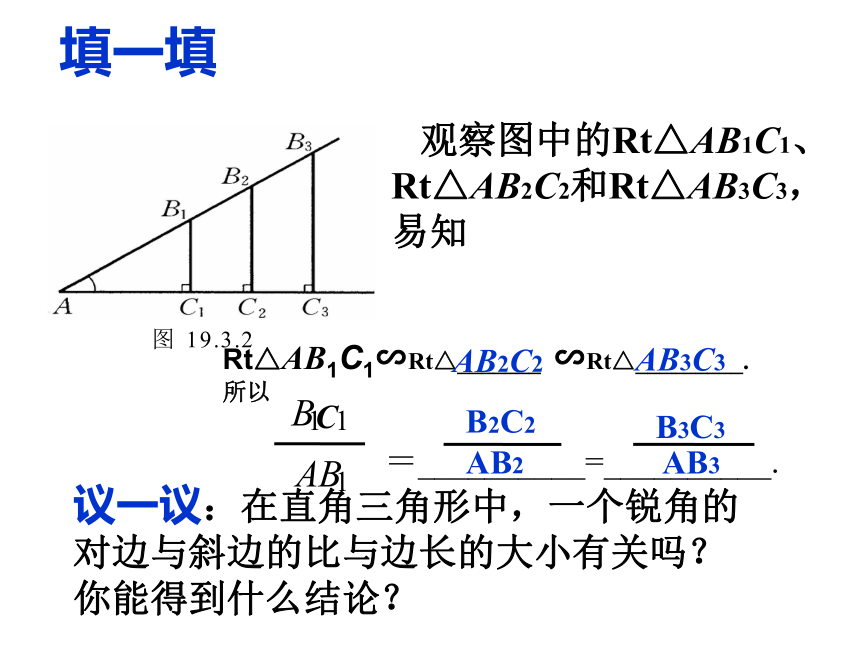
究当∠A=60°时当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值吗? 当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值呢?猜一猜AB3C3Rt△AB1C1∽Rt△_______ ∽Rt△_________.
所以 议一议:在直角三角形中,一个锐角的对边与斜边的比与边长的大小有关吗?
你能得到什么结论?填一填AB2C2 观察图中的Rt△AB1C1、
Rt△AB2C2和Rt△AB3C3,
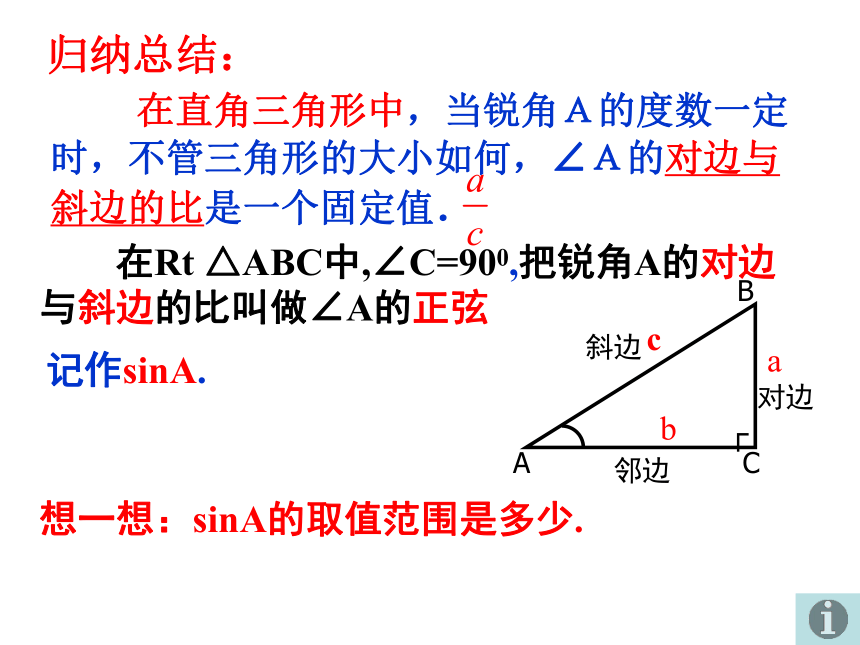
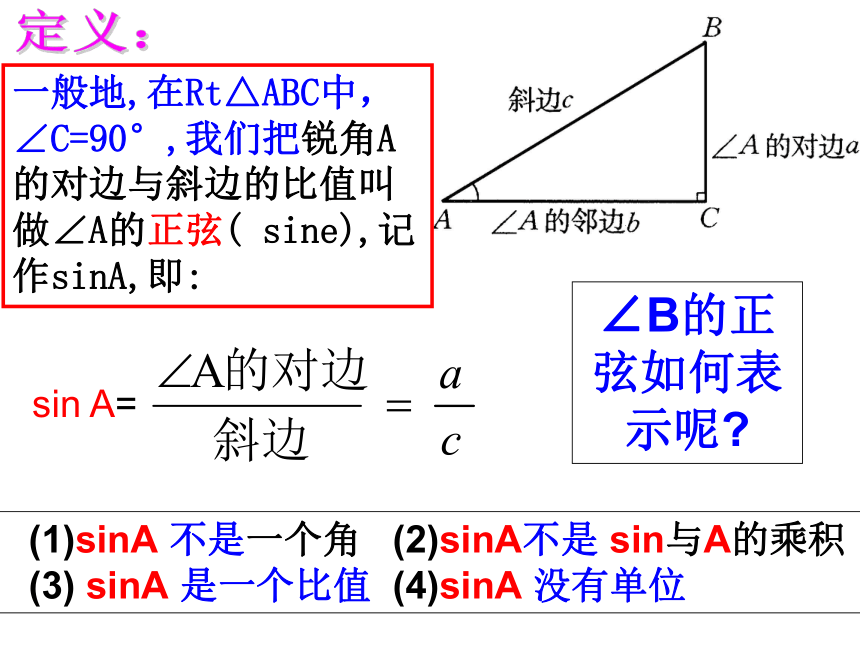
易知想一想:sinA的取值范围是多少.归纳总结: 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值. 在Rt △ABC中,∠C=900,把锐角A的对边与斜边的比叫做∠A的正弦记作sinA.一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:sin A= ∠B的正弦如何表示呢?(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积
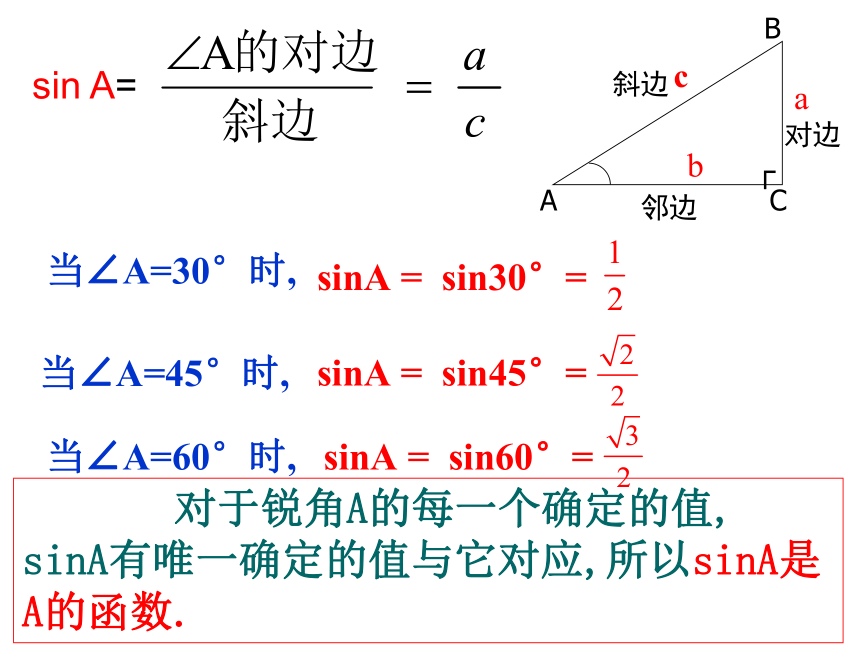
(3) sinA 是一个比值 (4)sinA 没有单位定义: 对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.当∠A=30°时,sinA = sin30°=当∠A=45°时,sinA = sin45°=sin A= 当∠A=60°时,sinA = sin60°=例1 如图,在Rt△ABC中,∠C=90°,求sinA和 sinB的值.解: (1)在Rt△ABC中,因此(2)在Rt△ABC中,因此ABCABC34135练一练1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√√××sinA是一个比值(注意比的顺序),无单位;2)如图,sinA= ( ) ×2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练根据下图,求sinA和sinB的值.C3课堂练习4、如图,P为角a的一边OA上的任一点,过P作PQ ⊥OB于点Q,则a的正弦函数值与( )
A、角a的大小无关 B、点P的位位置无关
C、角a的度数无关 D、OP的长度有关OPABQa5、如图,∠C=900,AB= ,BC= ,
求sin A 的值。BCA
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。6、如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB的值.解: ∵∠B=∠ACD ∴sinB=sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴sinB==41.在△ABC中,∠C=900,sinA+sinB=
,AC+BC=28,求AB的长.应用新知2、如图,在△ABC中, AB=BC=5,
sinA= ,求△ABC 的面积。3.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.C练一练4.已知点P(3,4)是∠ 边OA上的一点求sin 的值?A5、在平面直角坐标系中,有一条直线l:
,l与x轴的正半轴的夹角为α,求sinα的值。成果检测ABCDE6.已知在RT△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=
AE=7,求DE的长.1.锐角三角函数定义:2.sinA是∠A的函数. Sin300 =sin45°=在直角三角形中探究 如图,在Rt△ABC中, ∠C=900,当锐角A确定时, ∠A的对边与斜边的比就随之确定,
此时,其他边之间的
比是否也确定了呢?
为什么?三角函数符号最早的使用1949年至今,由于受前苏联教材的影响,我国数学书籍中“cot”改为“ctg”,“tan”改为“tg”,其余四个符号均未变。这就是为什么我国市场上流行的进口函数计算器上有“tan”而无“tg”按键的缘故。小资料sine(正弦)一词始于阿拉伯人雷基奥蒙坦。他是十五世纪西欧数学界的领导
人物,他于1464年完成的著作《论各种三角形》,1533年开始发行,这是一
本纯三角学的书,使三角学脱离天文学,独立成为一门数学分科。Cosine(余弦)及cotangent(余切)为英国人根日尔首先使用,最早在1620年伦敦出版的他所著的《炮兵测量学》中出现。Secant(正割)及tangent(正切)为丹麦数学家托马斯·劳克首创,最早见于
他的《圆几何学》一书中。Cosecant(余割)一词为锐梯卡斯所创。最早见于他1596年出版的《宫廷乐章》一书。1626年,阿尔贝特·格洛德最早推出简写的三角符号:“sin” ,“tan” ,“sec”.
1675年,英国人奥屈特最早推出余下的简写三角符号:“cos”,“cot”,“csc”。便直到1748年,经过数学家欧拉的引用后,才逐渐通用起来。
境
探
究当∠A=30°时问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是45°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
究当∠A=45°时问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是60°,为使出水口的高度为35m,那么需要准备多长的水管?ABC情
境
探
究当∠A=60°时当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值吗? 当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值呢?猜一猜AB3C3Rt△AB1C1∽Rt△_______ ∽Rt△_________.
所以 议一议:在直角三角形中,一个锐角的对边与斜边的比与边长的大小有关吗?
你能得到什么结论?填一填AB2C2 观察图中的Rt△AB1C1、
Rt△AB2C2和Rt△AB3C3,
易知想一想:sinA的取值范围是多少.归纳总结: 在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比是一个固定值. 在Rt △ABC中,∠C=900,把锐角A的对边与斜边的比叫做∠A的正弦记作sinA.一般地,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比值叫做∠A的正弦( sine),记作sinA,即:sin A= ∠B的正弦如何表示呢?(1)sinA 不是一个角 (2)sinA不是 sin与A的乘积
(3) sinA 是一个比值 (4)sinA 没有单位定义: 对于锐角A的每一个确定的值, sinA有唯一确定的值与它对应,所以sinA是A的函数.当∠A=30°时,sinA = sin30°=当∠A=45°时,sinA = sin45°=sin A= 当∠A=60°时,sinA = sin60°=例1 如图,在Rt△ABC中,∠C=90°,求sinA和 sinB的值.解: (1)在Rt△ABC中,因此(2)在Rt△ABC中,因此ABCABC34135练一练1.判断对错:1) 如图 (1) sinA= ( )
(2)sinB= ( )
(3)sinA=0.6m ( )
(4)SinB=0.8 ( )
√√××sinA是一个比值(注意比的顺序),无单位;2)如图,sinA= ( ) ×2.在Rt△ABC中,锐角A的对边和斜边同时扩大
100倍,sinA的值( )
A.扩大100倍 B.缩小
C.不变 D.不能确定C练一练根据下图,求sinA和sinB的值.C3课堂练习4、如图,P为角a的一边OA上的任一点,过P作PQ ⊥OB于点Q,则a的正弦函数值与( )
A、角a的大小无关 B、点P的位位置无关
C、角a的度数无关 D、OP的长度有关OPABQa5、如图,∠C=900,AB= ,BC= ,
求sin A 的值。BCA
求一个角的正弦值,除了用定义直接求外,还可以转化为求和它相等角的正弦值。6、如图, ∠C=90°CD⊥AB.
sinB可以由哪两条线段之比?想一想若AC=5,CD=3,求sinB的值.解: ∵∠B=∠ACD ∴sinB=sin∠ACD在Rt△ACD中,AD=sin ∠ACD=∴sinB==41.在△ABC中,∠C=900,sinA+sinB=
,AC+BC=28,求AB的长.应用新知2、如图,在△ABC中, AB=BC=5,
sinA= ,求△ABC 的面积。3.已知△ABC中,∠ACB=900,CD⊥AB于D,若AB=5,BC=4,求sinα的值.C练一练4.已知点P(3,4)是∠ 边OA上的一点求sin 的值?A5、在平面直角坐标系中,有一条直线l:
,l与x轴的正半轴的夹角为α,求sinα的值。成果检测ABCDE6.已知在RT△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=
AE=7,求DE的长.1.锐角三角函数定义:2.sinA是∠A的函数. Sin300 =sin45°=在直角三角形中探究 如图,在Rt△ABC中, ∠C=900,当锐角A确定时, ∠A的对边与斜边的比就随之确定,
此时,其他边之间的
比是否也确定了呢?
为什么?三角函数符号最早的使用1949年至今,由于受前苏联教材的影响,我国数学书籍中“cot”改为“ctg”,“tan”改为“tg”,其余四个符号均未变。这就是为什么我国市场上流行的进口函数计算器上有“tan”而无“tg”按键的缘故。小资料sine(正弦)一词始于阿拉伯人雷基奥蒙坦。他是十五世纪西欧数学界的领导
人物,他于1464年完成的著作《论各种三角形》,1533年开始发行,这是一
本纯三角学的书,使三角学脱离天文学,独立成为一门数学分科。Cosine(余弦)及cotangent(余切)为英国人根日尔首先使用,最早在1620年伦敦出版的他所著的《炮兵测量学》中出现。Secant(正割)及tangent(正切)为丹麦数学家托马斯·劳克首创,最早见于
他的《圆几何学》一书中。Cosecant(余割)一词为锐梯卡斯所创。最早见于他1596年出版的《宫廷乐章》一书。1626年,阿尔贝特·格洛德最早推出简写的三角符号:“sin” ,“tan” ,“sec”.
1675年,英国人奥屈特最早推出余下的简写三角符号:“cos”,“cot”,“csc”。便直到1748年,经过数学家欧拉的引用后,才逐渐通用起来。
