28.1 锐角三角函数2
文档属性
| 名称 | 28.1 锐角三角函数2 |

|
|
| 格式 | rar | ||
| 文件大小 | 613.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-21 00:00:00 | ||
图片预览





文档简介
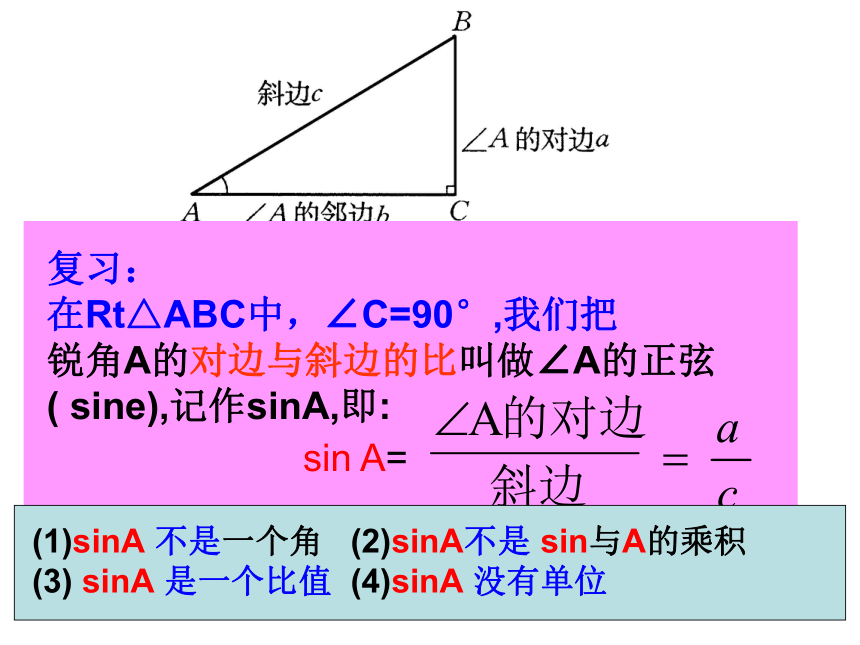
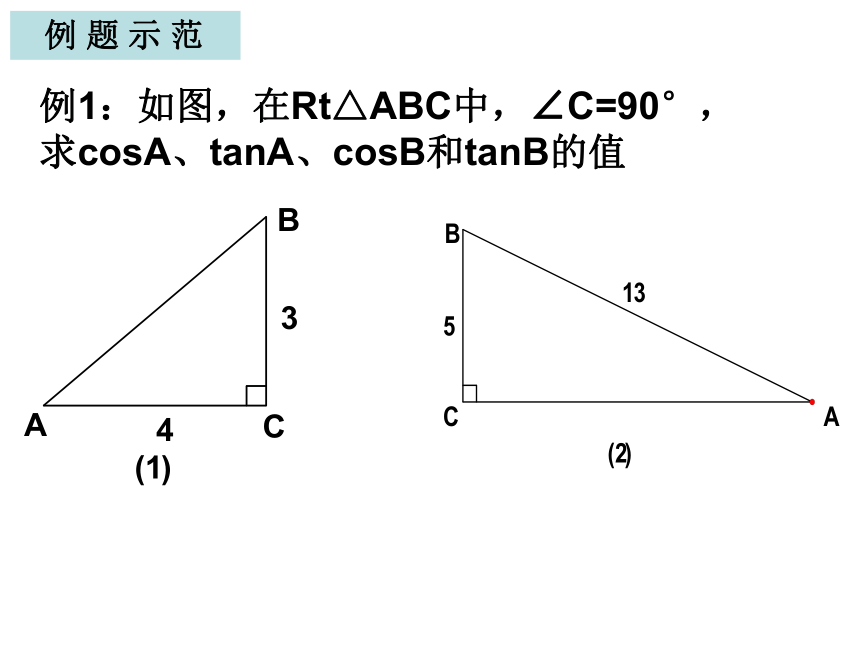
课件18张PPT。28.1 锐角三角函数(2)义务教育课程标准实验教科书九年级 上册人民教育出版社sin A= 如图,在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么? 当锐角A的大小确定时,∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的,我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即 把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.例1:如图,在Rt△ABC中,∠C=90°,求cosA、tanA、cosB和tanB的值 例 题 示 范 例2 如图,在Rt△ABC中,∠C=90°,BC=6,sinA= ,求
cosA、tanB的值.解:∵又 例 题 示 范 例3、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.练 习2. 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?3. 如图,在Rt△ABC中,∠C=90°,AC=
8,tanA= , 求:sinA、cosB的值.1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.练 习解:由勾股定理2. 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?解:设各边长分别为a、b、c,∠A的三个三角函数分别为则扩大2倍后三边分别为2a、2b、2c3. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,
求:sinA、cosB的值.ABC8解:4.已知锐角α的始边在x轴的正半轴上,
(顶点在原点)终边上一点P的坐标为(2, 3),
求角α的三个三角函数值。M解:过P作OM⊥x轴于M,则OM=2,PM=3sinα= ,
cosα= ,tanα= ,(1)Rt△ABC中,∠C=900,sinA=,则cosA =_______. tanA= .
(2)Rt△ABC中,∠C=900,若AC∶AB=1∶3,
则tanA= .
(3)如图,在△ABC中,若∠ACB=900,且CD⊥AB于D,用线段的比表示∠а的余弦值:___________。1.下图中∠ACB=90°,CD⊥AB,垂足为D.
指出∠A和∠B的对边、邻边.试一试:CDABBCACADABBCCD如图,在△ABC中,AD、BE分别是边BC、AC的高,且BF=4,AC=3,求tan∠BAD的值cosB= ,sinB= , tanB = .sinA= ,cosA= ,tanA= . 观察探究如图,已知在△ABC中,∠C= 90°BC=5,AC=12
求∠A,∠B的三个三角函数. 判断:
① sinA+ sinB = sin(A+B) ( )
② cosA+cosB = cos(A+B) ( )××练习 :1. 在Rt△ABC中,∠C=Rt∠,BC:AC=1:2,则sinA= 。2.如图, 在Rt△ABC中,∠B=Rt∠,b= c= ,则sin(90°-A)= 。45°45°在Rt△ABC中定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
cosA、tanB的值.解:∵又 例 题 示 范 例3、在△ABC中,AB=AC=4,BC=6,求∠B的三角函数值。1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.练 习2. 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?3. 如图,在Rt△ABC中,∠C=90°,AC=
8,tanA= , 求:sinA、cosB的值.1. 分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.练 习解:由勾股定理2. 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?解:设各边长分别为a、b、c,∠A的三个三角函数分别为则扩大2倍后三边分别为2a、2b、2c3. 如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,
求:sinA、cosB的值.ABC8解:4.已知锐角α的始边在x轴的正半轴上,
(顶点在原点)终边上一点P的坐标为(2, 3),
求角α的三个三角函数值。M解:过P作OM⊥x轴于M,则OM=2,PM=3sinα= ,
cosα= ,tanα= ,(1)Rt△ABC中,∠C=900,sinA=,则cosA =_______. tanA= .
(2)Rt△ABC中,∠C=900,若AC∶AB=1∶3,
则tanA= .
(3)如图,在△ABC中,若∠ACB=900,且CD⊥AB于D,用线段的比表示∠а的余弦值:___________。1.下图中∠ACB=90°,CD⊥AB,垂足为D.
指出∠A和∠B的对边、邻边.试一试:CDABBCACADABBCCD如图,在△ABC中,AD、BE分别是边BC、AC的高,且BF=4,AC=3,求tan∠BAD的值cosB= ,sinB= , tanB = .sinA= ,cosA= ,tanA= . 观察探究如图,已知在△ABC中,∠C= 90°BC=5,AC=12
求∠A,∠B的三个三角函数. 判断:
① sinA+ sinB = sin(A+B) ( )
② cosA+cosB = cos(A+B) ( )××练习 :1. 在Rt△ABC中,∠C=Rt∠,BC:AC=1:2,则sinA= 。2.如图, 在Rt△ABC中,∠B=Rt∠,b= c= ,则sin(90°-A)= 。45°45°在Rt△ABC中定义中应该注意的几个问题: 1、sinA、cosA、tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形)。 2、sinA、 cosA、tanA是一个比值(数值)。 3、sinA、 cosA 、tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
