28.1锐角三角函数复习
文档属性
| 名称 | 28.1锐角三角函数复习 |

|
|
| 格式 | rar | ||
| 文件大小 | 362.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-21 00:00:00 | ||
图片预览




文档简介
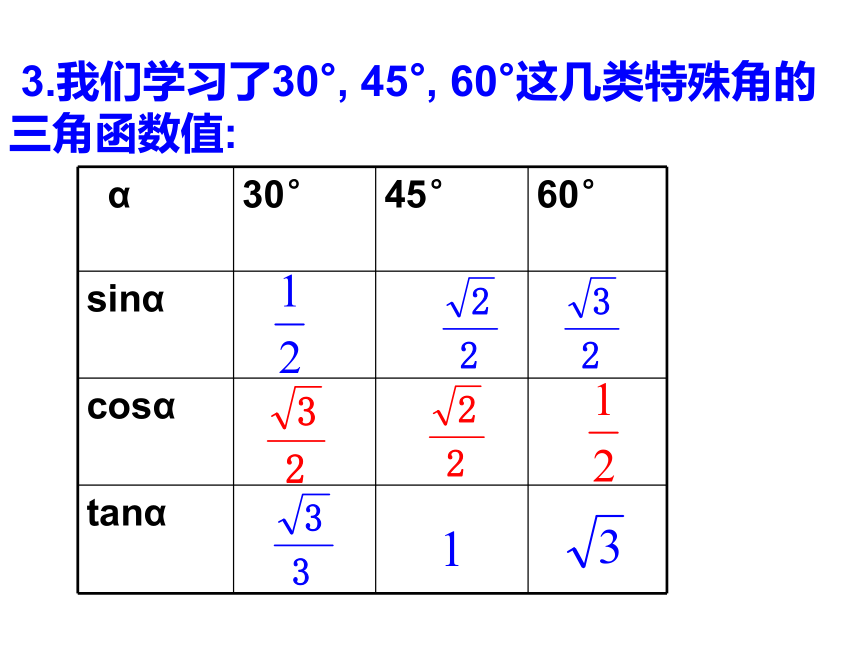
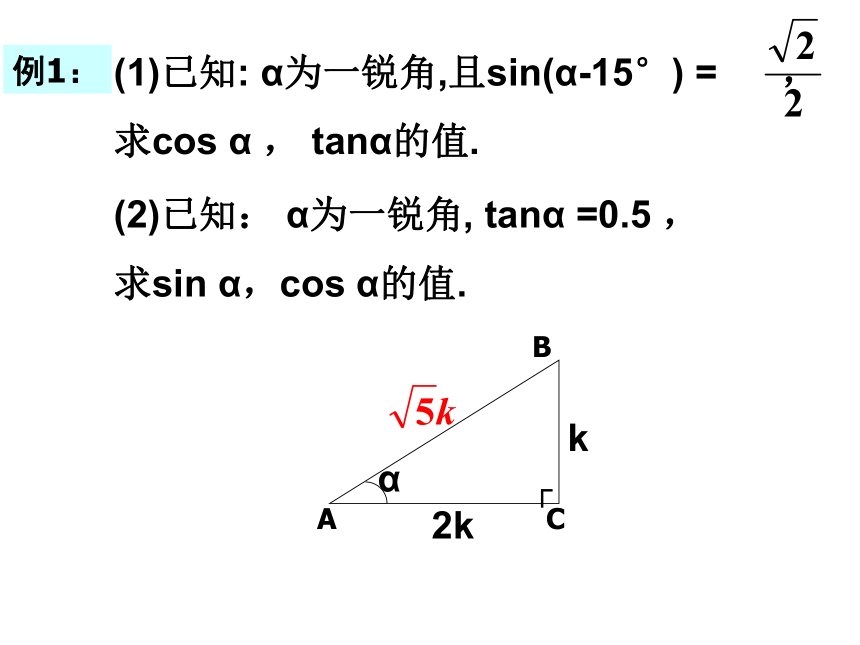
课件16张PPT。28.1 锐角三角函数(复习巩固)义务教育课程标准实验教科书九年级 上册人民教育出版社复习: 1.锐角三角函数的定义: 在 中, ∠A的余弦 :∠A的正弦:互余两角之间的三角函数关系:同角之间的三角函数关系:特殊角300,450,600角的三角函数值.2.性质: ◆范围:00sinA=cosB,tanA●tanB=1.sin2A+cos2A=1. 3.我们学习了30°, 45°, 60°这几类特殊角的三角函数值: 例1:(2)已知: α为一锐角, tanα =0.5 ,
求sin α,cos α的值.(1)已知: α为一锐角,且sin(α-15°) = ,
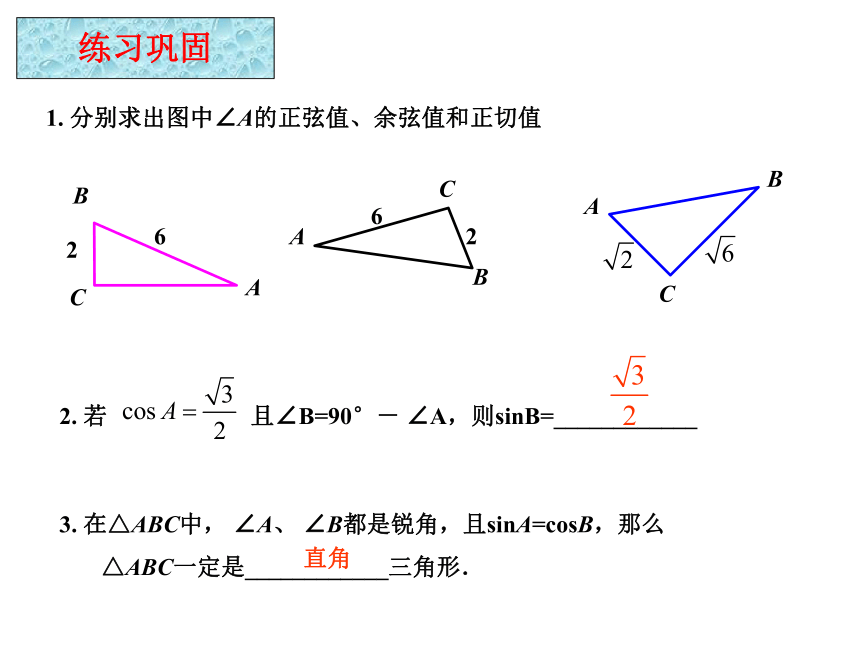
求cos α , tanα的值.k2k2. 若 且∠B=90°- ∠A,则sinB=____________3. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么
△ABC一定是____________三角形.直角练习巩固1. 分别求出图中∠A的正弦值、余弦值和正切值(4)4、计算:例题2
在Rt△ABC中,∠C=90°,化简(∠ A <45°)
1. α是锐角,且sinα+cosα= ,则sinα·cosα
等于( )
(A) (B) (C) (D) 12.若∠A为锐角,且sinA= ,那么( )
(A)0°<∠A<30 ° (B)30°<∠A<45°
(C)45°<∠A<60° (D)60°<∠A<90°3. 已知sinα·cosα= ,45°<α<90°,
则cosα-sinα= .CB练习巩固0⑶ tan44°tan46°=( ).1(4)tan29°tan60°tan61°=( ).14.⑴ 已知:Rt△ABC中,∠C=90°∠A为锐角,且tanA=0.6,tanB=( ).⑵ sin2A+tanAtanB -2+cos2A=( )(5) sin53°cos37°+cos53°sin37°=( )例3:在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。H思考:求tan22.5°的值。1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且DA= AC,求∠ABD的三个三角函数值。练习2、Rt△BAC中,∠ACB=900,sinB= D是BC上一点,DE⊥AB于E,CD=DE,AC+CD=9,分别求BC、DE的长,3.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.D4.已知在Rt△ABC中,∠C=900,
D是BC中点,DE⊥AB,垂足为E,
sin∠BDE= AE=7,求DE的长.5. 如图,在RT△ABC中,∠C=900,若tanA+tanB=4,S△ABC=8.求斜边AB的长.6. 如图,△ABC中,∠C=900,BD平分∠ABC,BC=12,BD= ,求∠A的度数及AD的长.
求sin α,cos α的值.(1)已知: α为一锐角,且sin(α-15°) = ,
求cos α , tanα的值.k2k2. 若 且∠B=90°- ∠A,则sinB=____________3. 在△ABC中, ∠A、 ∠B都是锐角,且sinA=cosB,那么
△ABC一定是____________三角形.直角练习巩固1. 分别求出图中∠A的正弦值、余弦值和正切值(4)4、计算:例题2
在Rt△ABC中,∠C=90°,化简(∠ A <45°)
1. α是锐角,且sinα+cosα= ,则sinα·cosα
等于( )
(A) (B) (C) (D) 12.若∠A为锐角,且sinA= ,那么( )
(A)0°<∠A<30 ° (B)30°<∠A<45°
(C)45°<∠A<60° (D)60°<∠A<90°3. 已知sinα·cosα= ,45°<α<90°,
则cosα-sinα= .CB练习巩固0⑶ tan44°tan46°=( ).1(4)tan29°tan60°tan61°=( ).14.⑴ 已知:Rt△ABC中,∠C=90°∠A为锐角,且tanA=0.6,tanB=( ).⑵ sin2A+tanAtanB -2+cos2A=( )(5) sin53°cos37°+cos53°sin37°=( )例3:在△ABC中,D是AB的中点,DC⊥AC,tan∠BCD=0.5,AB=4 ,求AC。H思考:求tan22.5°的值。1、Rt△BAC中,∠C=900,CA=CB
D是AC上一点,且DA= AC,求∠ABD的三个三角函数值。练习2、Rt△BAC中,∠ACB=900,sinB= D是BC上一点,DE⊥AB于E,CD=DE,AC+CD=9,分别求BC、DE的长,3.△ABC中,AB=8,BC=6,S△ABC=12,试求sinB的值.D4.已知在Rt△ABC中,∠C=900,
D是BC中点,DE⊥AB,垂足为E,
sin∠BDE= AE=7,求DE的长.5. 如图,在RT△ABC中,∠C=900,若tanA+tanB=4,S△ABC=8.求斜边AB的长.6. 如图,△ABC中,∠C=900,BD平分∠ABC,BC=12,BD= ,求∠A的度数及AD的长.
