正切函数的图像和性质
图片预览



文档简介
课件19张PPT。1.4.3正切函数的图象及性质 我们已经学习了正弦、余弦函数的图像
我们是怎么得到其的图像的呢?一、复习回顾思考 利用单位圆中的三角函数线作图
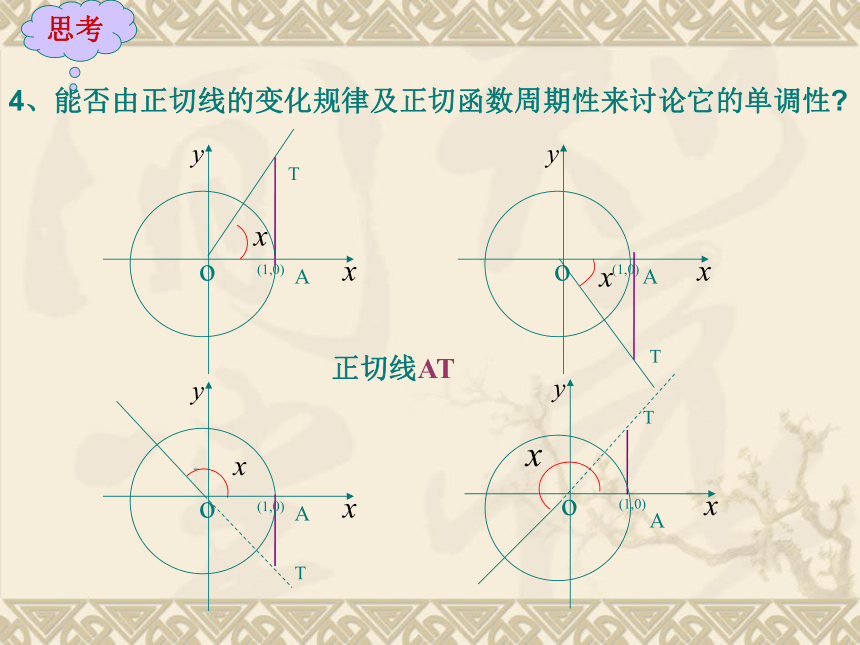
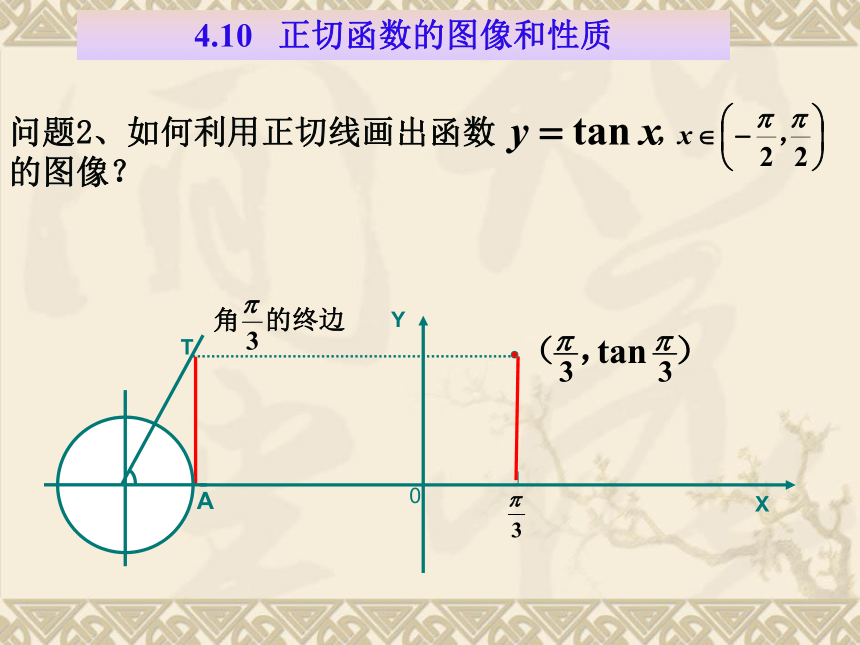
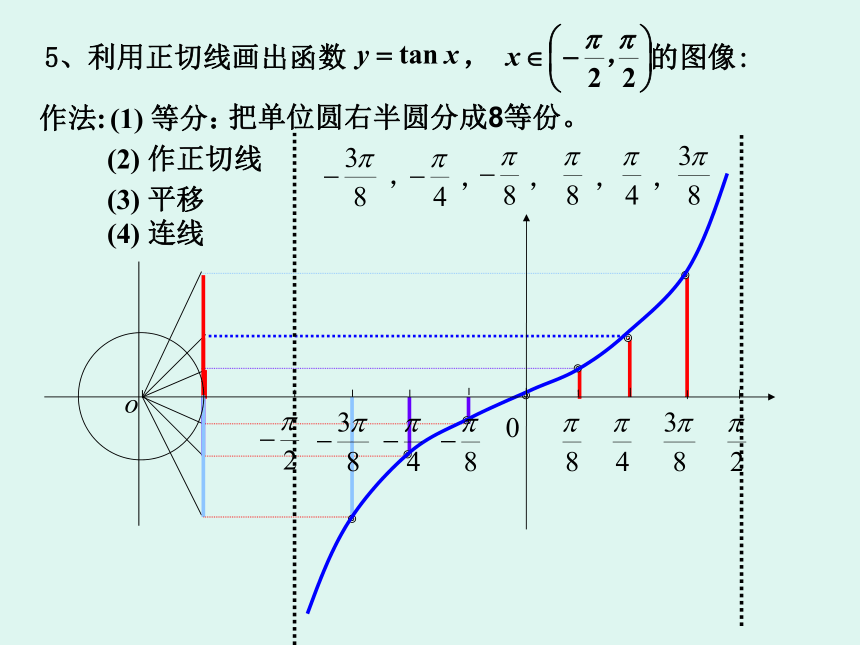
(由一个周期到整个定义域)1、利用正切函数的定义,说出正切函数的定义域; ∴ 是周期函数, 是它的一个周期. 思考由诱导公式知2、正切函数 是否为周期函数? 3、正切函数 是否具有奇偶性? 思考由诱导公式知正切函数是奇函数. 4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?思考AT正切线ATATATAT4.10 正切函数的图像和性质问题2、如何利用正切线画出函数 , 的图像? 作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。5、利用正切线画出函数 , 的图像: 6、利用正切函数的周期性,把图象向左,右扩展,得到正切函数叫做正切曲线.从图中可以看出,正切曲线是由被相互平行的直线所隔的无穷多支曲线组成的.yx1-1?/2-?/2?3?/2-3?/2-?0定义域值域周期性奇偶性单调性 RT= ?奇函数 函数y=tanx增区间二:性质tt+?t-?你能从正切函数的图象出发,讨论它的性质吗?(1)正切函数是整个定义域上的增函数吗?为什么?(2)正切函数会不会在某一区间内是减函数?为什么? 问题: 在每一个开区间
, 内都是增函数。问 题 讨 论例1 求函数 的定义域那么函数 的定义域是:
所以由 可得:
所以函数 的定义域是:四、灵活运用解:令换元例2 求下列函数的周期:由上面两例,你能得到函数y=Atan(ωx+Ф)的周期吗(提示:利用正切函数的最小正周期 来解) 例3 求下列函数的单调区间:例3.比较下列各组数的大小 1 . tan1670 与 tan1730解:900<1670<1730<1800
又有y=tanx, 在(900,2700)上是增函数 所以:tan1670例4.观察正切曲线,写出满足下列条件的x的值的范围。
(1) tanx >1 (2)tanx
?/2–?/2–?/2?/200xxy?/4y1?/2课堂练习:<1、求函数y=tan3x的定义域 . >3、观察正切曲线。写出满足下列条件的x值的范围
(1)若 则 .
若 ,则 .
(3)若 ,则 。 解:观察正切曲线,写出满足条件的 的取值范围小结:
1.正切曲线的几何画法以及正切函数的性质
2.正切函数性质
3.用数形结合的思想理解和处理有关的问题. 性质作业p73.1、4、5
我们是怎么得到其的图像的呢?一、复习回顾思考 利用单位圆中的三角函数线作图
(由一个周期到整个定义域)1、利用正切函数的定义,说出正切函数的定义域; ∴ 是周期函数, 是它的一个周期. 思考由诱导公式知2、正切函数 是否为周期函数? 3、正切函数 是否具有奇偶性? 思考由诱导公式知正切函数是奇函数. 4、能否由正切线的变化规律及正切函数周期性来讨论它的单调性?思考AT正切线ATATATAT4.10 正切函数的图像和性质问题2、如何利用正切线画出函数 , 的图像? 作法:(1) 等分:(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成8等份。5、利用正切线画出函数 , 的图像: 6、利用正切函数的周期性,把图象向左,右扩展,得到正切函数叫做正切曲线.从图中可以看出,正切曲线是由被相互平行的直线所隔的无穷多支曲线组成的.yx1-1?/2-?/2?3?/2-3?/2-?0定义域值域周期性奇偶性单调性 RT= ?奇函数 函数y=tanx增区间二:性质tt+?t-?你能从正切函数的图象出发,讨论它的性质吗?(1)正切函数是整个定义域上的增函数吗?为什么?(2)正切函数会不会在某一区间内是减函数?为什么? 问题: 在每一个开区间
, 内都是增函数。问 题 讨 论例1 求函数 的定义域那么函数 的定义域是:
所以由 可得:
所以函数 的定义域是:四、灵活运用解:令换元例2 求下列函数的周期:由上面两例,你能得到函数y=Atan(ωx+Ф)的周期吗(提示:利用正切函数的最小正周期 来解) 例3 求下列函数的单调区间:例3.比较下列各组数的大小 1 . tan1670 与 tan1730解:900<1670<1730<1800
又有y=tanx, 在(900,2700)上是增函数 所以:tan1670
(1) tanx >1 (2)tanx
?/2–?/2–?/2?/200xxy?/4y1?/2课堂练习:<1、求函数y=tan3x的定义域 . >3、观察正切曲线。写出满足下列条件的x值的范围
(1)若 则 .
若 ,则 .
(3)若 ,则 。 解:观察正切曲线,写出满足条件的 的取值范围小结:
1.正切曲线的几何画法以及正切函数的性质
2.正切函数性质
3.用数形结合的思想理解和处理有关的问题. 性质作业p73.1、4、5
