9.2锐角三角比

9.1锐角三角比
山东单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一学习目标：
1通过实例认识直角三角形的边角关系。
2理解锐角三角比的概念。
3已知直角三角形的两边，会求一个锐角的三角比。
4感知锐角三角比在实际生活中的应用，提高理论联系实际的意识。
二知识回顾：
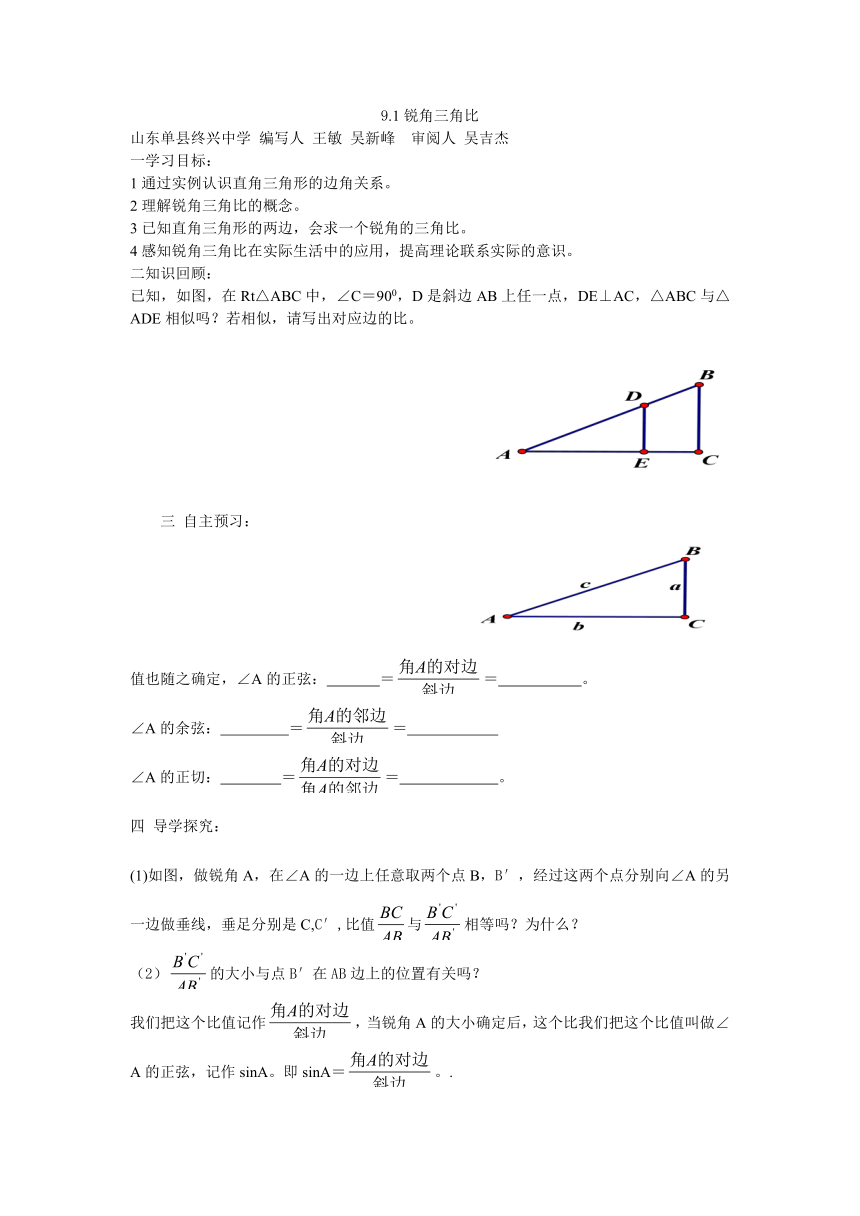
已知，如图，在Rt△ABC中，∠C＝900，D是斜边AB上任一点，DE⊥AC，△ABC与△ADE相似吗？若相似，请写出对应边的比。
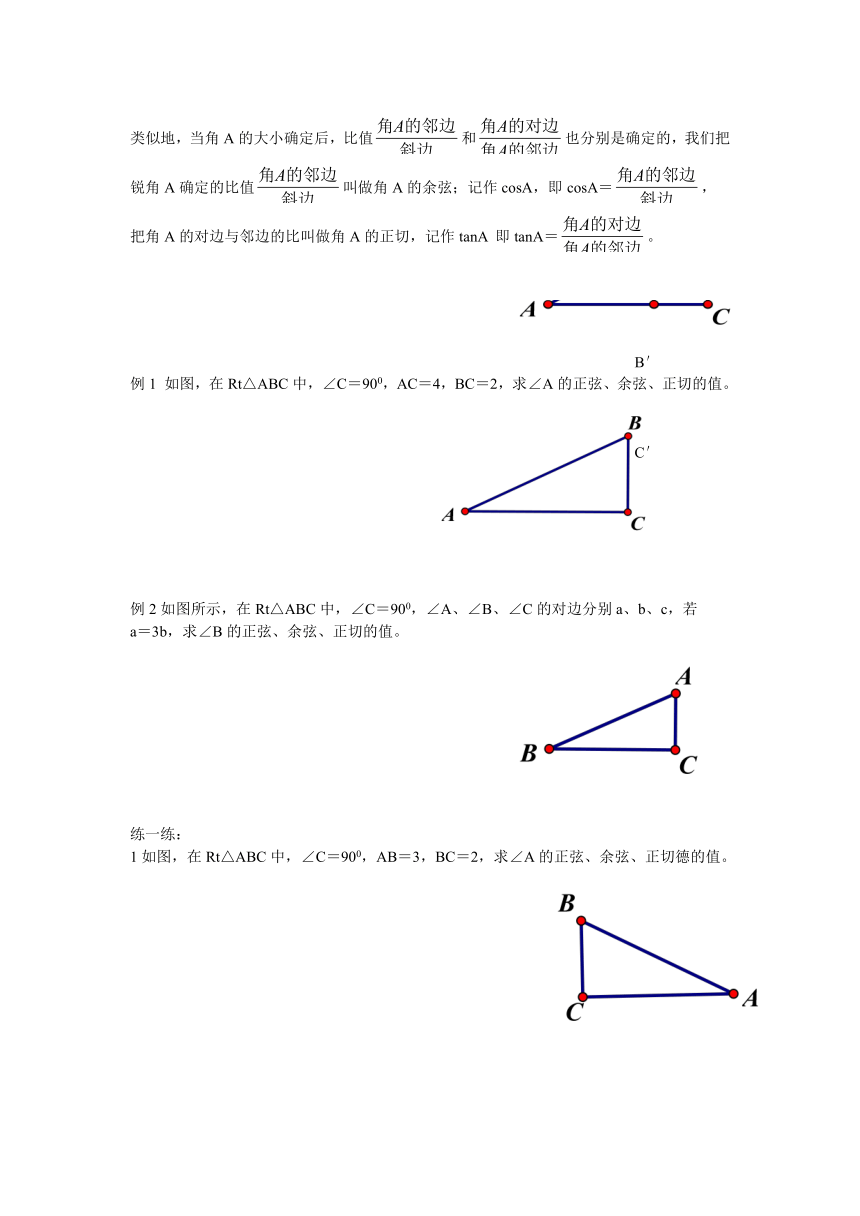
三 自主预习：
值也随之确定，∠A的正弦： ＝＝ 。
∠A的余弦： ＝＝
∠A的正切： ＝＝ 。
四 导学探究：
(1)如图，做锐角A，在∠A的一边上任意取两个点B，B′，经过这两个点分别向∠A的另一边做垂线，垂足分别是C,C′,比值与相等吗？为什么？
（2）的大小与点B′在AB边上的位置有关吗？
我们把这个比值记作，当锐角A的大小确定后，这个比我们把这个比值叫做∠A的正弦，记作sinA。即sinA＝。.
类似地，当角A的大小确定后，比值和也分别是确定的，我们把锐角A确定的比值叫做角A的余弦；记作cosA，即cosA＝，
把角A的对边与邻边的比叫做角A的正切，记作tanA 即tanA＝。
例1 如图，在Rt△ABC中，∠C＝900，AC＝4，BC＝2，求∠A的正弦、余弦、正切的值。
例2如图所示，在Rt△ABC中，∠C＝900，∠A、∠B、∠C的对边分别a、b、c，若
a＝3b，求∠B的正弦、余弦、正切的值。
练一练：
1如图，在Rt△ABC中，∠C＝900，AB＝3，BC＝2，求∠A的正弦、余弦、正切德的值。
2如1题图，在Rt△ABC中，∠C＝900，AB＝8，cosA＝，则AC＝ ，BC＝ 。
五 当堂达标：
1 如图，P是∠α的边OA上一点，且P的坐标为（3,4），则sinα的值为（ ）
A B C D
2 在Rt⊿ABC中，∠C=900，BC=2，sinA=,则边AB的长为 。
3在Rt⊿ABC中，∠C=900，BC=2，sinA=，则cosB的值等于（ ）
A B C D
4在Rt⊿ABC中，∠C=900，AB=3，BC=2，则cosA的值是 。
5在Rt⊿ABC中，∠C=900，∠C=900，a=1,b=,则tanA等于（ ）
A B C D
6在Rt⊿ABC中，∠C=900，a,b,c分别是∠A,∠B,∠C的对边，若b=2a,则tanA=
7 如图，CD是Rt⊿ABC斜边上的高，AC=4，BC=3，则cos∠BCD的值是（ ）
A B C D
(7题) (8题) （9题）
8 如图，Rt⊿ABC中，∠C=900，BC=1，AB=2，则下列结论正确的是（ ）
A sinA= B tanA= C cosB= D tanB=
9 如图，在⊿ABC中，∠ACB=900，CD⊥AB于D,若AC=2，AB=3，则tan∠BCD=( )
A B C D
10 已知Rt⊿ABC中，∠C=900，sinA= ，则tanB=（ ）
A B C D
11 如图，在Rt⊿ABC中，∠C=900，AM是BC边上的中线，sin∠CAM=,则tanB的值为
。
12 如图，⊿ABC中，AB=AC, ∠A=450，AC的垂直平分线分别交AB、AC于D、E两点，连接CD,如果AD=1，那么tan∠BCD= 。
(11题) （12题）
解答题
1 已知α为锐角，tanα= ，求∠α的其他三角比。
能力提升
如图，在Rt⊿ABC中，∠C=900，BC,AC,AB三边的长分别为a,b,c，则sinA=
，cosA=,tanA=,
(1)试根据定义并结合勾股定理探求sinA、cosA、tanA之间存在的一般关系，并说明理由。
（2）利用上面探索的结论解答下面问题，若∠A为锐角，sinA=，求cosA。
B′
C′
3
4
P
O
x
y
α