全等三角形判定sas（2）

课件18张PPT。教学目标：通过画图、操作、实验、观察等数学活动，探索三角形全等的判定方法。
了解判定方法SAS，能初步运用它判定两个三角形全等。
在运用判定方法的过程中，培养学生的合情推理能力。“角边角”以及“角角边”都是通过两个三角形的三对元素对应相等来判定三角形全等的。除此之外，在两个三角形中，三对元素对应相等的情况还有哪几种？还有三种情况，它们是两边一角、三条边和
三个角分别对应相等。这三种情况都能判定
两个三角形全等吗？本节课我们先来探究利
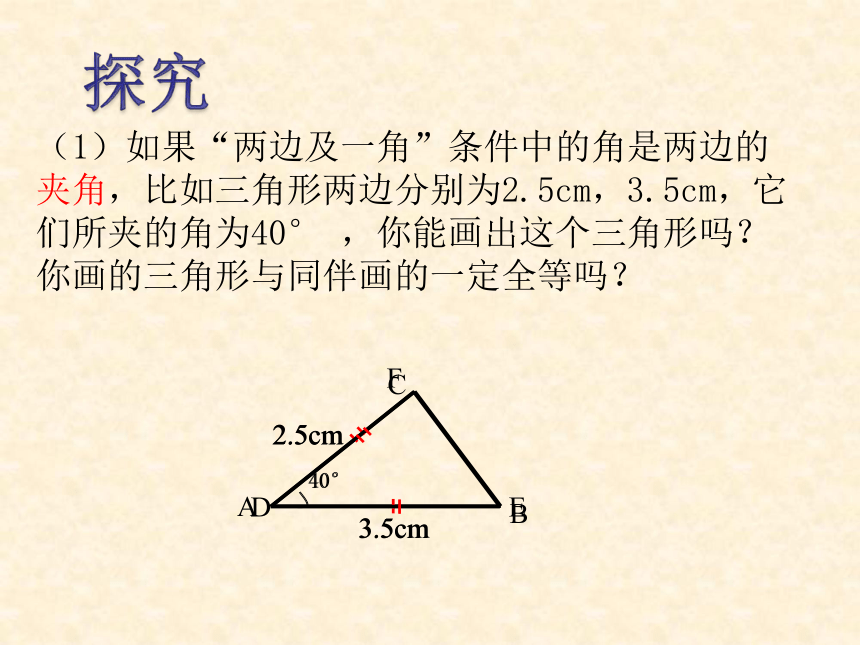
用两边一角，能否判定两个三角形全等。（1）如果“两边及一角”条件中的角是两边的夹角，比如三角形两边分别为2.5cm，3.5cm，它们所夹的角为40° ，你能画出这个三角形吗？你画的三角形与同伴画的一定全等吗？探究1. 画∠MA′ N = ∠AABCMNA ′2. 在射线 A M ，A N 上分别取 A ′B ′ = AB ，
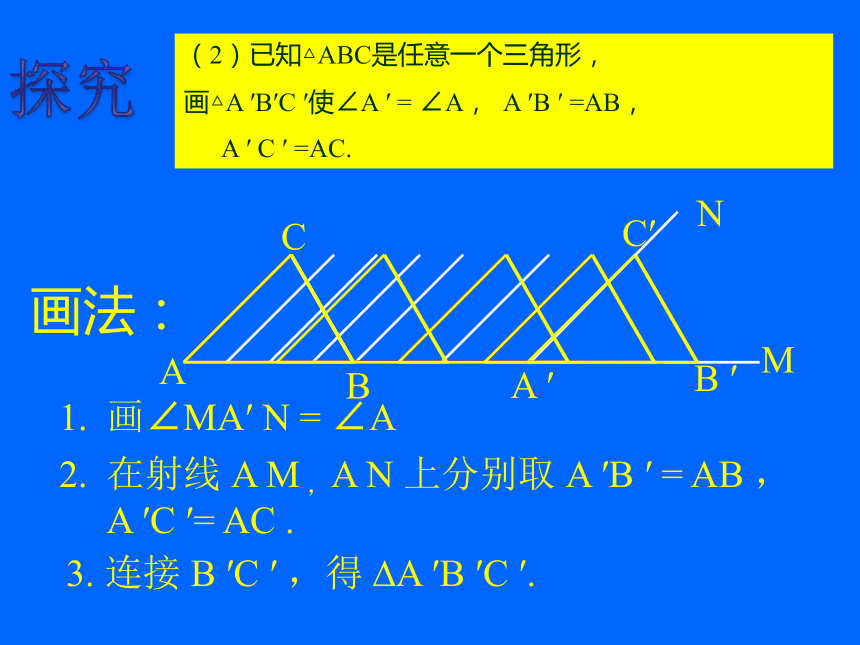
A ′C ′= AC .B ′C′3. 连接 B ′C ′ ，得 ?A ′B ′C ′.（2）已知△ABC是任意一个三角形，
画△A ′B′C ′使∠A ′ = ∠A， A ′B ′ =AB，
A ′ C ′ =AC.画法：探究边角边定理 如果一个三角形的两条边及其夹角与另一个三角形的两条边及其夹角分别相等，那么这两个三角形全等。
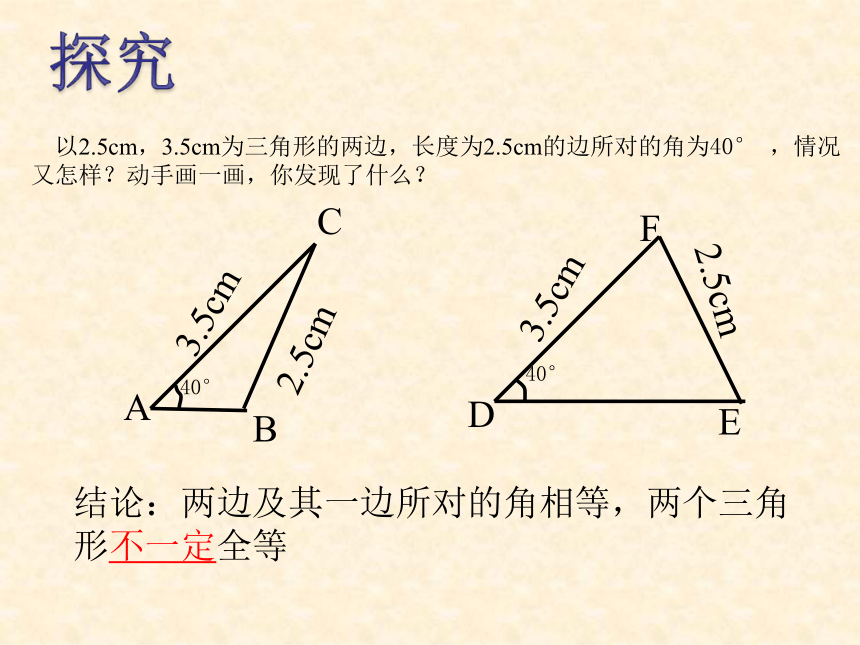
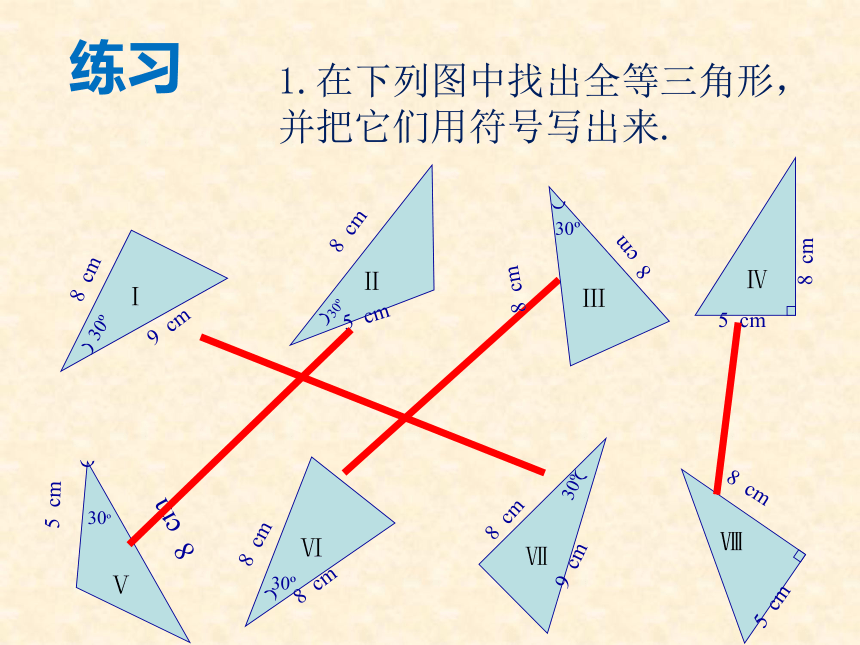
可以简写成 “边角边” 或“ SAS ” 归纳 以2.5cm，3.5cm为三角形的两边，长度为2.5cm的边所对的角为40° ，情况又怎样？动手画一画，你发现了什么？ABCDEF2.5cm3.5cm40°40°3.5cm2.5cm结论：两边及其一边所对的角相等，两个三角形不一定全等探究1.在下列图中找出全等三角形，
并把它们用符号写出来.练习BCDEA如图，已知AB＝AC，AD＝AE。
求证：∠B＝∠CCEABAD证明：在△ABD和△ACE中∴△ABD≌△ACE（SAS）
∴∠B＝∠C（全等三角形
对应角相等）思考与讨论一FEDCBA如图，∠B＝∠E，AB＝EF
BD＝EC，那么△ABC与　
△FED全等吗？为什么？解：全等。∵BD=EC（已知）　　　
∴BD－CD＝EC－CD。
即BC＝ED　　在△ABC与△FED中∴△ABC≌△FED（SAS）AC∥FD吗？为什么？∴∠1＝∠2∴∠3＝∠4∴AC∥FD（内错角相等，两直线平行43）21（思考与讨论二思考与讨论三 如图线段AB是一个池塘的长度，现在想测量这个池塘的长度，在水上测量不方便，你有什么好的方法较方便地把池塘的长度测量出来吗？想想看。AB 小明的设计方案：先在池塘旁取一个能直接到达A和B处的点C，连结AC并延长至D点，使AC=DC，连结BC并延长至E点，使BC=EC，连结CD，用米尺测出DE的长，这个长度就等于A，B两点的距离。请你说明理由。ABCED 理由： AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS)
AB=DE在下列推理中填写需要补充的条件，使结论成立：
(1)如图，在△AOB和△DOC中AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC（ ）∠ AOB∠ DOC对顶角相等SAS思考与讨论四（2）如图，在△AEC和△ADB中，____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB（ ）AEADACABSAS已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
ABCD证明:在△ACB 和 △ADB中 AC = A D
∠CAB=∠DAB
A B = A B (公共边）∴△ACB≌△ADB（SAS）例题解析.若AB=AC，则添加什么条件可得△ABD≌ △ACD?△ABD≌ △ACDAD=ADAB=AC∠BAD= ∠CADSAS 练习三.已知如图，点D 在AB上，点E在AC上，BE与CD交于点O，△ABE≌ △ACDSASAB=AC∠A= ∠ AAD=AE要证△ABE≌ △ACD需添加什么条件? 练习四.已知如图，点D 在AB上，点E在AC上，BE与CD交于点O，SASOB=OC∠BOD= ∠ COEOD=OE要证△BOD≌ △COE需添加什么条件?△BOD≌ △COE课堂小结1.边角边公理：有两边和它们的______对应相等的两个三角形全等（SAS）夹角2.边角边公理的发现过程所用到的数学方法（包括画 图、猜想、分析、归纳等.)3.边角边公理的应用中所用到的数学方法:
证明线段（或角相等） 证明线段（或角）所在的两个三角形全等.转化 1. 证明两个三角形全等所需的条件应按对应边、对应角、对应边顺序书写.
2. 公理中所出现的边与角必须在所证明的两个三角形中.
3. 公理中涉及的角必须是两边的夹角.用公理证明两个三角形全等需注意