18.1勾股定理(2)
图片预览


文档简介
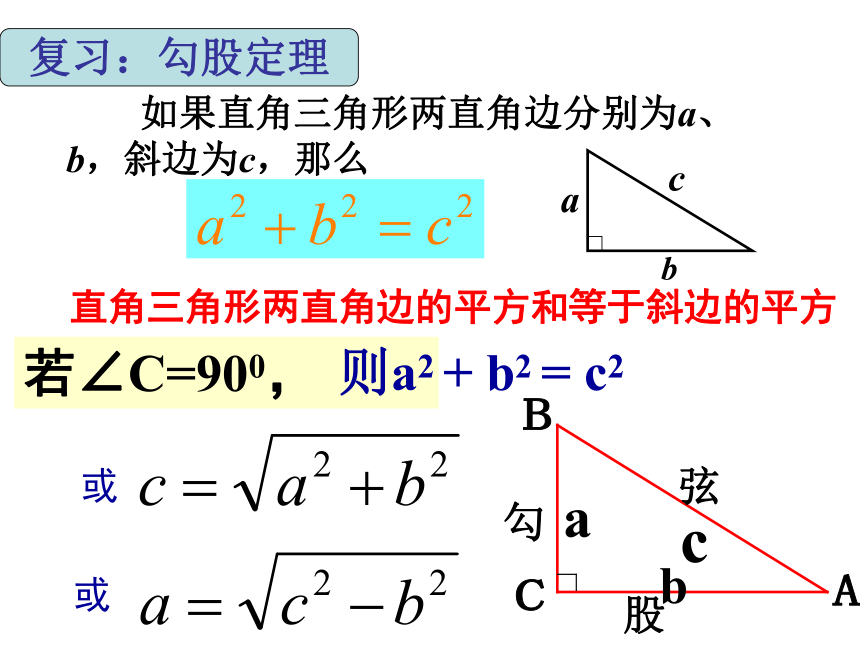
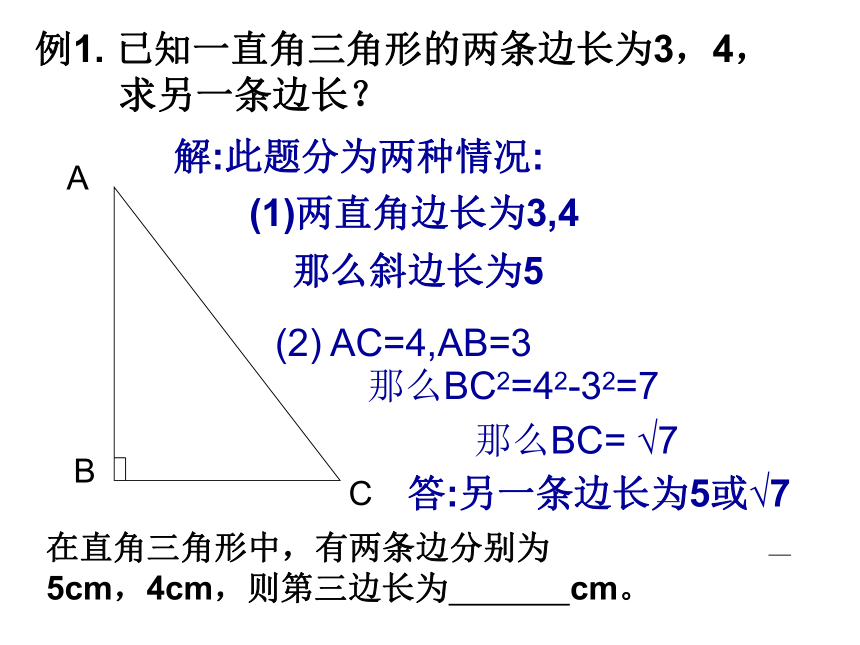
课件22张PPT。 如果直角三角形两直角边分别为a、b,斜边为c,那么直角三角形两直角边的平方和等于斜边的平方若∠C=900,则a2 + b2 = c2或或复习:勾股定理 例1. 已知一直角三角形的两条边长为3,4,
求另一条边长?(1)两直角边长为3,4AB那么斜边长为5(2) AC=4,AB=3那么BC2=42-32=7那么BC= √7C解:此题分为两种情况:答:另一条边长为5或√7
在直角三角形中,有两条边分别为
5cm,4cm,则第三边长为 cm。例2、在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b ;
已知: a=7, c=8, 求b .例3、一直角三角形的一直角边长为7, 另两条边
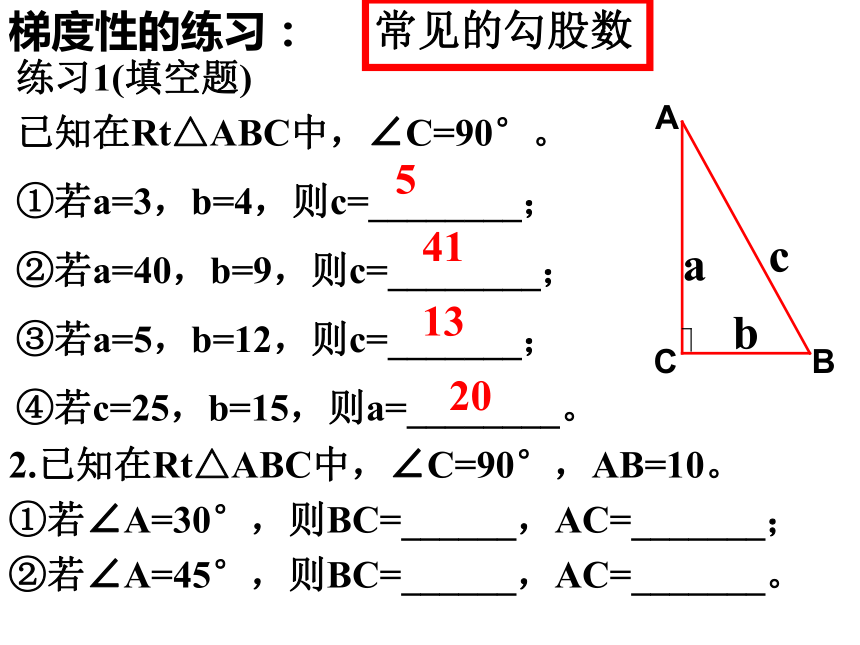
长为两个连续整数,求这个直角三角形的周长.练习1(填空题)
已知在Rt△ABC中,∠C=90°。
①若a=3,b=4,则c=________;
②若a=40,b=9,则c=________;
③若a=5,b=12,则c=_______;
④若c=25,b=15,则a=________。梯度性的练习: 常见的勾股数54113202.已知在Rt△ABC中,∠C=90°,AB=10。
①若∠A=30°,则BC=______,AC=_______;
②若∠A=45°,则BC=______,AC=_______。2.已知:∠C=900, a:b=3:4,
c=10,a= __ 和 b=___3.已知:△ABC, AB=AC=17,BC=16,
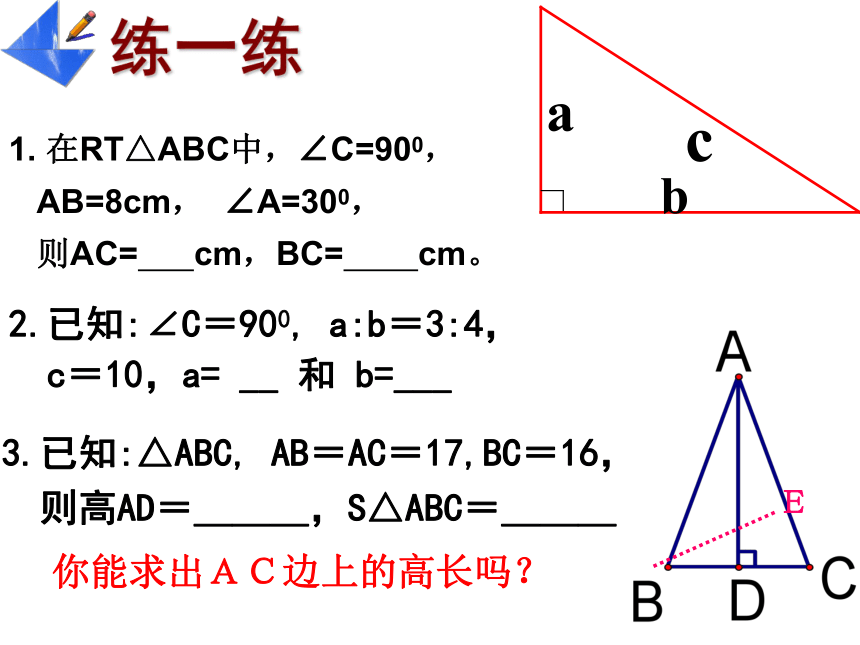
则高AD=___,S△ABC=___你能求出AC边上的高长吗?E1. 在RT△ABC中,∠C=900,
AB=8cm, ∠A=300,
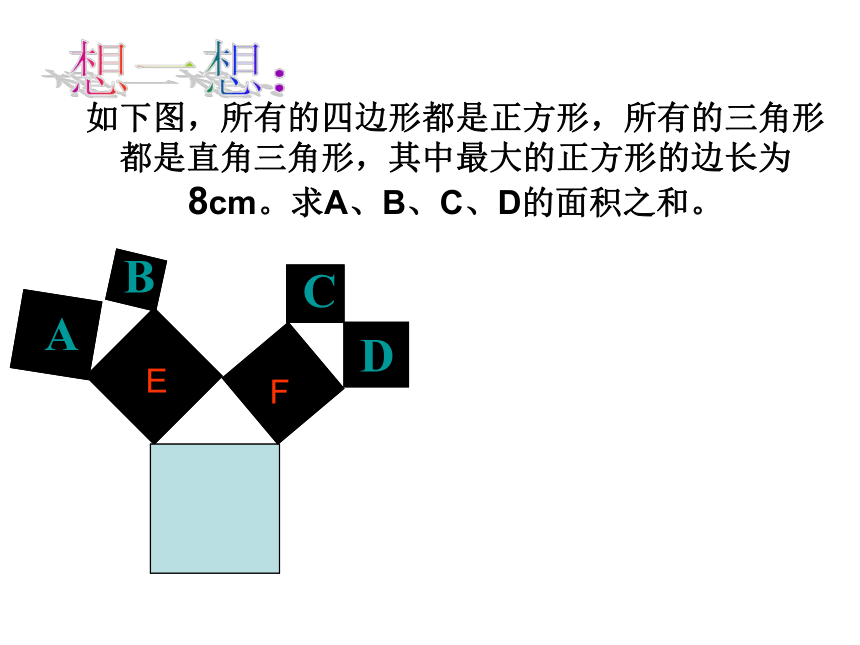
则AC= cm,BC= cm。想一想:如下图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为
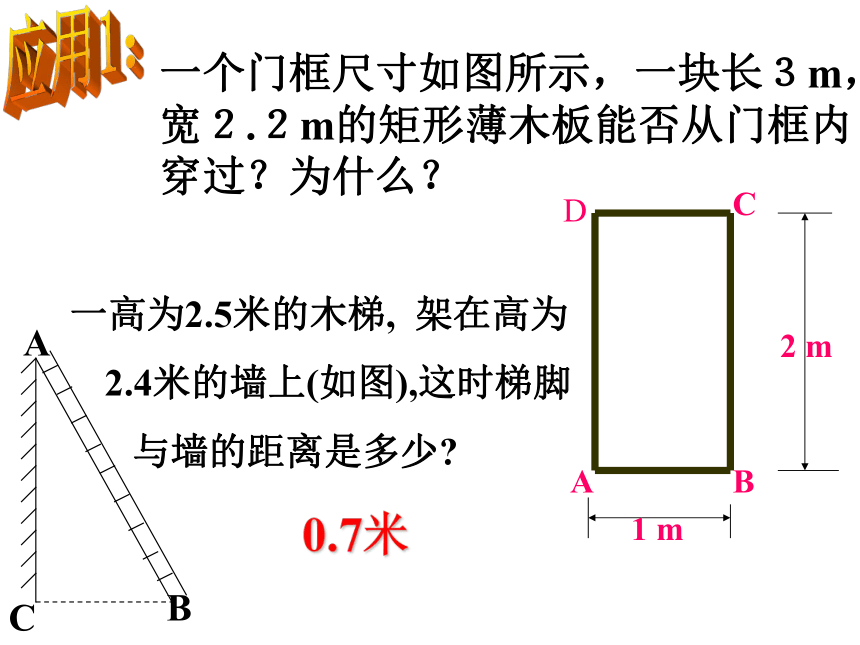
8cm。求A、B、C、D的面积之和。EEEEF一个门框尺寸如图所示,一块长3m,宽2.2m的矩形薄木板能否从门框内穿过?为什么?应用1: 一高为2.5米的木梯, 架在高为
2.4米的墙上(如图),这时梯脚
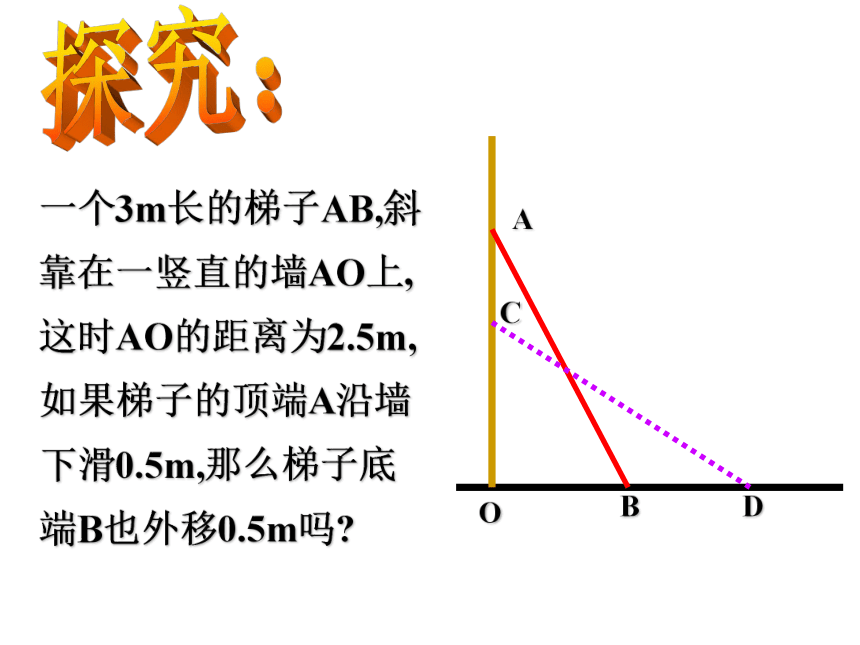
与墙的距离是多少? 0.7米探究:ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?分析:DB=OD-OB,求BD,可以 先求OB,OD.梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?练3、放学以后,小红和小颖从学校
分手,分别沿着东方向和南方向回家,
若小红和小颖行走的速度都是40米/分,
小红用15分钟到家,小颖用20分钟到家,
小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定C 例1、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?A4000米5000米20秒后BC例2.一辆卡车装满货物后,能否通过如图所示的工厂门(上方为半圆)?卡车高3.0m,宽1.6m。请说明你的理由。ABC2m2.3m能力升级?????????如图,在棱长为10厘米的正方体的
一个顶点A处有一只蚂蚁,现要向
顶点B处爬行,已知蚂蚁爬行的速
度是1厘米/秒,且速度保持不变,
问蚂蚁能否在20秒内从A爬到B?BAB约22秒 棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,
现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,
且速度保持不变,问蚂蚁能否在20秒内从A爬到B?如改为:有一个圆拄,它的高为12cm,底面半
径为3cm,在圆拄下底面的A点有一只蚂蚁,
它想吃到上底面与A相对的B点处的食物,
沿圆拄侧面爬行的最短路程是 。ABDA补练2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形28厘米试一试 如图,一根旗杆在离地5米处断裂,旗杆顶部落在离旗杆底部12米处.旗杆折断之前有多高?5米12米应用三:小明妈妈买了一部29英寸(约74厘米)的电视机。小明量了电视机屏幕后,发现屏幕只有约58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗? 我们利用数格子的方法得到:即直角三角形两直角边的平方和等于斜边的平方A的面积+B的面积=C的面积a2+b2=c2从而探索了直角三角形的三边关系,得到勾股定理:
求另一条边长?(1)两直角边长为3,4AB那么斜边长为5(2) AC=4,AB=3那么BC2=42-32=7那么BC= √7C解:此题分为两种情况:答:另一条边长为5或√7
在直角三角形中,有两条边分别为
5cm,4cm,则第三边长为 cm。例2、在直角三角形ABC中, ∠C=900,
已知: a=5, b=12, 求c;
已知: b=6,c=10 , 求a;
已知: a=7, c=25, 求b ;
已知: a=7, c=8, 求b .例3、一直角三角形的一直角边长为7, 另两条边
长为两个连续整数,求这个直角三角形的周长.练习1(填空题)
已知在Rt△ABC中,∠C=90°。
①若a=3,b=4,则c=________;
②若a=40,b=9,则c=________;
③若a=5,b=12,则c=_______;
④若c=25,b=15,则a=________。梯度性的练习: 常见的勾股数54113202.已知在Rt△ABC中,∠C=90°,AB=10。
①若∠A=30°,则BC=______,AC=_______;
②若∠A=45°,则BC=______,AC=_______。2.已知:∠C=900, a:b=3:4,
c=10,a= __ 和 b=___3.已知:△ABC, AB=AC=17,BC=16,
则高AD=___,S△ABC=___你能求出AC边上的高长吗?E1. 在RT△ABC中,∠C=900,
AB=8cm, ∠A=300,
则AC= cm,BC= cm。想一想:如下图,所有的四边形都是正方形,所有的三角形
都是直角三角形,其中最大的正方形的边长为
8cm。求A、B、C、D的面积之和。EEEEF一个门框尺寸如图所示,一块长3m,宽2.2m的矩形薄木板能否从门框内穿过?为什么?应用1: 一高为2.5米的木梯, 架在高为
2.4米的墙上(如图),这时梯脚
与墙的距离是多少? 0.7米探究:ACOBD一个3m长的梯子AB,斜
靠在一竖直的墙AO上,
这时AO的距离为2.5m,
如果梯子的顶端A沿墙
下滑0.5m,那么梯子底
端B也外移0.5m吗?分析:DB=OD-OB,求BD,可以 先求OB,OD.梯子的顶端沿墙下滑0.5m,梯子底端外移_______.在Rt△AOB中,在Rt△COD中,OD-OB = 2.236 -1.658 ≈0.580.58 m一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?练3、放学以后,小红和小颖从学校
分手,分别沿着东方向和南方向回家,
若小红和小颖行走的速度都是40米/分,
小红用15分钟到家,小颖用20分钟到家,
小红和小颖家的距离为 ( )
A、600米 B、800米
C、1000米 D、不能确定C 例1、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?A4000米5000米20秒后BC例2.一辆卡车装满货物后,能否通过如图所示的工厂门(上方为半圆)?卡车高3.0m,宽1.6m。请说明你的理由。ABC2m2.3m能力升级?????????如图,在棱长为10厘米的正方体的
一个顶点A处有一只蚂蚁,现要向
顶点B处爬行,已知蚂蚁爬行的速
度是1厘米/秒,且速度保持不变,
问蚂蚁能否在20秒内从A爬到B?BAB约22秒 棱长为10厘米的正方体的一个顶点A处有一只蚂蚁,
现要向顶点B处爬行,已知蚂蚁爬行的速度是1厘米/秒,
且速度保持不变,问蚂蚁能否在20秒内从A爬到B?如改为:有一个圆拄,它的高为12cm,底面半
径为3cm,在圆拄下底面的A点有一只蚂蚁,
它想吃到上底面与A相对的B点处的食物,
沿圆拄侧面爬行的最短路程是 。ABDA补练2、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE提示构造直角三角形28厘米试一试 如图,一根旗杆在离地5米处断裂,旗杆顶部落在离旗杆底部12米处.旗杆折断之前有多高?5米12米应用三:小明妈妈买了一部29英寸(约74厘米)的电视机。小明量了电视机屏幕后,发现屏幕只有约58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗? 我们利用数格子的方法得到:即直角三角形两直角边的平方和等于斜边的平方A的面积+B的面积=C的面积a2+b2=c2从而探索了直角三角形的三边关系,得到勾股定理:
