九年级数学第三章《圆》检测题
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
九年级数学第三章《圆》检测题
(时间:60分钟,满分:100分)
一、选择题:(每小题4分,共20分)
1.⊙O的直径是15㎝,CD经过圆心O,与⊙O交于C、D两点,垂直弦AB于M,且OM:OC=3 :5,则AB=( )
A.24㎝ B.12㎝ C.6㎝ D.3㎝
2.⊙O的直径是3,直线与⊙O相交,圆心O到直线的距离是d,则d应满足( )
A.d>3 B.1.53.已知两圆的半径分别为R,r(R>r),圆心距为d,且R2+d2-r2=2Rd,则这两圆的位置关系是( )
A.内含B.相切C.相交D.相离
4.若直径为4㎝,6㎝的两个圆相外切,那么与这两个圆都相切且半径为5㎝的圆的个数是( )
A.5个 B.4个 C.3个 D.2个
5.圆内接正方形与该圆的内接正六边形的周长比为( )
A.2:3 B.: C.:2 D.2:3
二、填空题:(每小题4分,共20分)
6.过⊙O内一点P的最长的弦是10㎝,最短的弦是8㎝,则OP和长为 ㎝。
7.如图弦AC,BD相交于E,并且,∠BEC=110°,则∠ACD的度数是 。
8.若三角形的周长为P,面积为S,其内切圆的半径为r,则r:S= 。
9.已知∠AOB=30°,M为OB边上一点,以M为圆心,2㎝为半径作⊙M与OA相切,切点为N,则△MON的面积为 。
10.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③……,则第n(n>1)个图形阴影部分的面积是 。
……
三、解答题:(每小题8分,共40分)
11.如图,AB是⊙O的直径,CF⊥AB交⊙O于E、F,连结AC交⊙O于D。 求证:CD·AD = DE·DF。
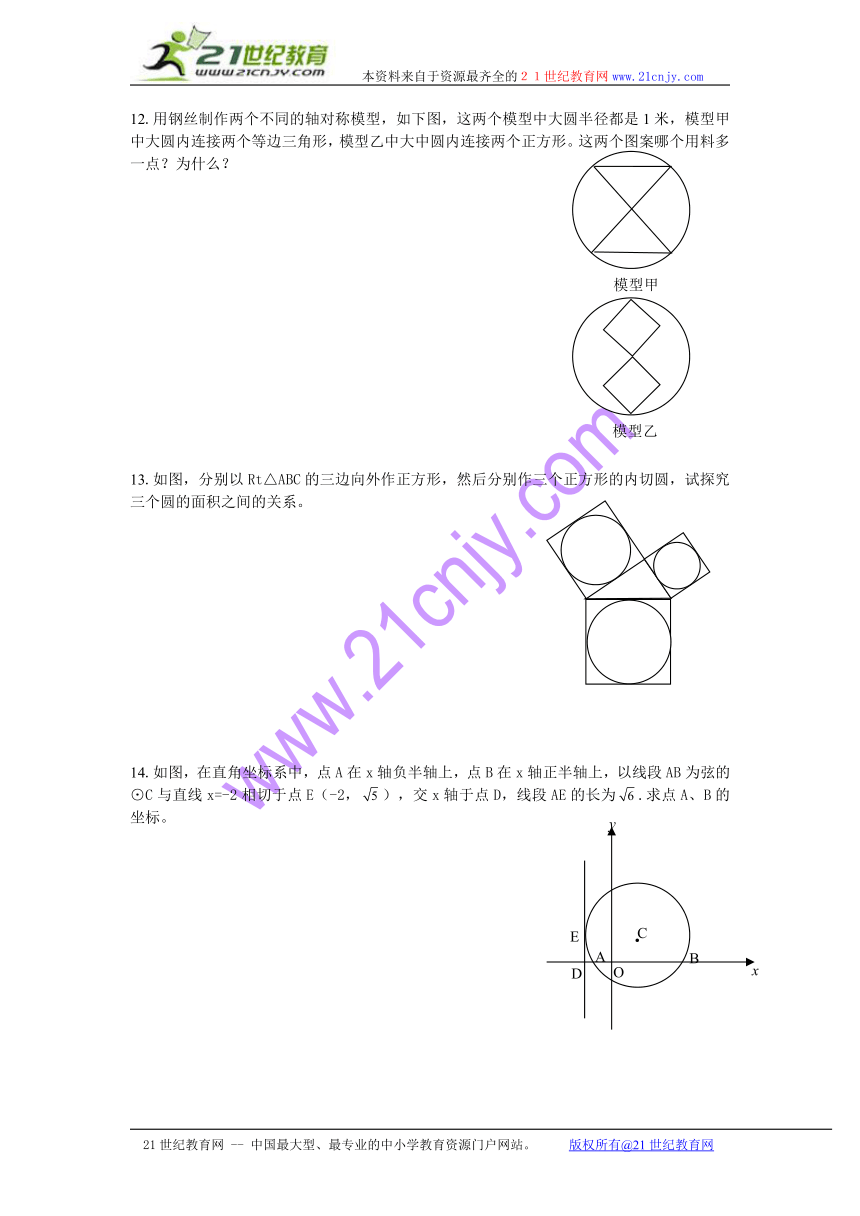
12.用钢丝制作两个不同的轴对称模型,如下图,这两个模型中大圆半径都是1米,模型甲中大圆内连接两个等边三角形,模型乙中大中圆内连接两个正方形。这两个图案哪个用料多一点?为什么?
13.如图,分别以Rt△ABC的三边向外作正方形,然后分别作三个正方形的内切圆,试探究三个圆的面积之间的关系。
14.如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,),交x轴于点D,线段AE的长为.求点A、B的坐标。
15.如图,四边形ABCD内接于圆,若AB=AC,且∠ABD=60°.求证:AB=BD+CD。
四、解答题:(每小题10分,共20分)
⊙16.已知:如图,AB为半圆O的直径,过圆心O作EO⊥AB,交半圆于F,过E作EC切⊙O于M,交AB的延长线于C,在EC上取一点 D,使CD=OC,请你判断DF与⊙O有什么关系,并证明你的判断的正确性。
17.如图,正三角形ABC的中心O恰好为扇形ODE的圆心,且点B在扇形内,要使扇形ODE绕点O无论怎样转动,△ABC与扇形重叠部分的面积总等于△ABC的面积的,扇形的圆心角应为多少度?说明你的理由。
检测题答案
一、选择题:(每小题4分,共20分)
BCBAD
二、填空题:(每小题4分,共20分)
6、3,7、75°,8、2:9,9、2㎝2,10、(1-)。
三、解答题:(每小题8分,共40分)
11.证明:连结AF,
∵AB中直径,CF⊥AB,
∴,
∴∠ADF=∠AFE,
∵A、D、E、F四点共圆,
∴∠CED=∠CAF=180°-∠DEF,
同理∠CDE=∠AFE,
∴∠CDE=∠ADF,
∴△CDE∽△FDA,
∴,∴CD·AD=DE·DF。
12.解:模型甲用料多一点。
理由:模型甲用料(2+6)米,模型乙用料(2+4)米,
∵4=,而6=,
∴2+6>2+4.
∴模型甲用料多一点。
13.解:设分别以AB、BC、CA为边长的正方形的内切圆面积分别为S1,S2,S3,
则S1==AB2,S2==BC2,S3==AC2
∵△ABC直角三角形,∴AB2=BC2+AC2.
∴AB2=BC2+AC2.
即S1=S2+S3。
14.解:连结EA,则Rt△ADE中,DE=,AE=,
∴DA=
∴OD=2,∴OA=OD-AD=1,
∴点A的坐标为(-1,0),
再连结EB,
∵∠DEA=∠B, ∠EDA=∠BDE,
∴,∴DB==5,
∴OB=DB-OD=5-2=3, ∴点B坐标为(3,0)。
15.证明:延长CD,使DE=BD,连结AE,
∵四边形ABCD内接于圆,
∴∠ADE=∠ABC=180°-∠ADC,
∵AB=AC,∴∠ABC=∠ACB,
∵∠ADB=∠ACB,∴∠ADB=∠ADE,
∵AD=AD
∴△ABD≌△AED,∴AB=AE,∴AC=AE,
∵∠ABD=∠ACD=60°,
∴△ACE是等边三角形,
∴CE=AE=AB,
∵CE=ED+DC=BD+CD,∴AB=BD+CD。
16.解:DF与⊙O相切。
证明:连结OM,
∵CD=CO,∴∠COD=∠CDO,
∵CE切⊙O于M,∴OM⊥CE,
∴∠C+∠COM=90°,
∵EO⊥AC,∴∠C+∠E=90°,
∴∠COM=∠E,
∵∠CDO=∠E+∠DOF, ∠COD=∠COM+∠DOM.
∴∠DOF=∠DOM,
∵OF=OM,OD=OD, ∴△OFD≌△OMD,
∴∠OFD=∠OMD=90°, ∴DF⊥OF, ∴DF与⊙O相切。
17.解:扇形的圆心角应为120°。
(1)当扇形的圆心角与正三角形的中心角重合时,显然△ABC与扇形重叠部分的面积等于△ABC的面积的。
(2)当扇形的圆心角与正三角形的中心角不重合时,连结OA、OB,设OD交AB于F,OE交BC于G,
∵O是正三角形的中心,
∴OA=OB,∠OAF=∠OBG,∠AOB=120°,
∴∠AOF=120°-∠BOF,∠BOG=∠DOE-∠BOF=120°-∠BOF,
∴∠AOF=∠BOG,
∴△AOF≌△BOG,
S四边形OFBG=S△OAB=S△ABC。
即扇形与△ABC的重叠部分的面积总等于△ABC的面积的。
由(1)(2)可知,当扇形的圆心角为120°时,△ABC与扇形重叠部分的面积总等于△ABC的面积的。
A
B
C
D
E
第7题
图②
图③
图①
A
F
B
E
C
D
O
·
模型甲
模型乙
A
D
E
O
B
x
y
·
C
A
B
C
D
F
E
D
M
·
A
O
B
C
D
E
O
C
A
B
A
F
B
E
C
D
O
·
A
D
E
O
B
x
y
·
C
A
B
C
D
E
F
E
D
M
·
A
O
B
C
D
E
O
C
A
B
F
G
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
九年级数学第三章《圆》检测题
(时间:60分钟,满分:100分)
一、选择题:(每小题4分,共20分)
1.⊙O的直径是15㎝,CD经过圆心O,与⊙O交于C、D两点,垂直弦AB于M,且OM:OC=3 :5,则AB=( )
A.24㎝ B.12㎝ C.6㎝ D.3㎝
2.⊙O的直径是3,直线与⊙O相交,圆心O到直线的距离是d,则d应满足( )
A.d>3 B.1.5
A.内含B.相切C.相交D.相离
4.若直径为4㎝,6㎝的两个圆相外切,那么与这两个圆都相切且半径为5㎝的圆的个数是( )
A.5个 B.4个 C.3个 D.2个
5.圆内接正方形与该圆的内接正六边形的周长比为( )
A.2:3 B.: C.:2 D.2:3
二、填空题:(每小题4分,共20分)
6.过⊙O内一点P的最长的弦是10㎝,最短的弦是8㎝,则OP和长为 ㎝。
7.如图弦AC,BD相交于E,并且,∠BEC=110°,则∠ACD的度数是 。
8.若三角形的周长为P,面积为S,其内切圆的半径为r,则r:S= 。
9.已知∠AOB=30°,M为OB边上一点,以M为圆心,2㎝为半径作⊙M与OA相切,切点为N,则△MON的面积为 。
10.如图①是半径为1的圆,在其中挖去2个半径为的圆得到图②,挖去22个半径为()2的圆得到图③……,则第n(n>1)个图形阴影部分的面积是 。
……
三、解答题:(每小题8分,共40分)
11.如图,AB是⊙O的直径,CF⊥AB交⊙O于E、F,连结AC交⊙O于D。 求证:CD·AD = DE·DF。
12.用钢丝制作两个不同的轴对称模型,如下图,这两个模型中大圆半径都是1米,模型甲中大圆内连接两个等边三角形,模型乙中大中圆内连接两个正方形。这两个图案哪个用料多一点?为什么?
13.如图,分别以Rt△ABC的三边向外作正方形,然后分别作三个正方形的内切圆,试探究三个圆的面积之间的关系。
14.如图,在直角坐标系中,点A在x轴负半轴上,点B在x轴正半轴上,以线段AB为弦的⊙C与直线x=-2相切于点E(-2,),交x轴于点D,线段AE的长为.求点A、B的坐标。
15.如图,四边形ABCD内接于圆,若AB=AC,且∠ABD=60°.求证:AB=BD+CD。
四、解答题:(每小题10分,共20分)
⊙16.已知:如图,AB为半圆O的直径,过圆心O作EO⊥AB,交半圆于F,过E作EC切⊙O于M,交AB的延长线于C,在EC上取一点 D,使CD=OC,请你判断DF与⊙O有什么关系,并证明你的判断的正确性。
17.如图,正三角形ABC的中心O恰好为扇形ODE的圆心,且点B在扇形内,要使扇形ODE绕点O无论怎样转动,△ABC与扇形重叠部分的面积总等于△ABC的面积的,扇形的圆心角应为多少度?说明你的理由。
检测题答案
一、选择题:(每小题4分,共20分)
BCBAD
二、填空题:(每小题4分,共20分)
6、3,7、75°,8、2:9,9、2㎝2,10、(1-)。
三、解答题:(每小题8分,共40分)
11.证明:连结AF,
∵AB中直径,CF⊥AB,
∴,
∴∠ADF=∠AFE,
∵A、D、E、F四点共圆,
∴∠CED=∠CAF=180°-∠DEF,
同理∠CDE=∠AFE,
∴∠CDE=∠ADF,
∴△CDE∽△FDA,
∴,∴CD·AD=DE·DF。
12.解:模型甲用料多一点。
理由:模型甲用料(2+6)米,模型乙用料(2+4)米,
∵4=,而6=,
∴2+6>2+4.
∴模型甲用料多一点。
13.解:设分别以AB、BC、CA为边长的正方形的内切圆面积分别为S1,S2,S3,
则S1==AB2,S2==BC2,S3==AC2
∵△ABC直角三角形,∴AB2=BC2+AC2.
∴AB2=BC2+AC2.
即S1=S2+S3。
14.解:连结EA,则Rt△ADE中,DE=,AE=,
∴DA=
∴OD=2,∴OA=OD-AD=1,
∴点A的坐标为(-1,0),
再连结EB,
∵∠DEA=∠B, ∠EDA=∠BDE,
∴,∴DB==5,
∴OB=DB-OD=5-2=3, ∴点B坐标为(3,0)。
15.证明:延长CD,使DE=BD,连结AE,
∵四边形ABCD内接于圆,
∴∠ADE=∠ABC=180°-∠ADC,
∵AB=AC,∴∠ABC=∠ACB,
∵∠ADB=∠ACB,∴∠ADB=∠ADE,
∵AD=AD
∴△ABD≌△AED,∴AB=AE,∴AC=AE,
∵∠ABD=∠ACD=60°,
∴△ACE是等边三角形,
∴CE=AE=AB,
∵CE=ED+DC=BD+CD,∴AB=BD+CD。
16.解:DF与⊙O相切。
证明:连结OM,
∵CD=CO,∴∠COD=∠CDO,
∵CE切⊙O于M,∴OM⊥CE,
∴∠C+∠COM=90°,
∵EO⊥AC,∴∠C+∠E=90°,
∴∠COM=∠E,
∵∠CDO=∠E+∠DOF, ∠COD=∠COM+∠DOM.
∴∠DOF=∠DOM,
∵OF=OM,OD=OD, ∴△OFD≌△OMD,
∴∠OFD=∠OMD=90°, ∴DF⊥OF, ∴DF与⊙O相切。
17.解:扇形的圆心角应为120°。
(1)当扇形的圆心角与正三角形的中心角重合时,显然△ABC与扇形重叠部分的面积等于△ABC的面积的。
(2)当扇形的圆心角与正三角形的中心角不重合时,连结OA、OB,设OD交AB于F,OE交BC于G,
∵O是正三角形的中心,
∴OA=OB,∠OAF=∠OBG,∠AOB=120°,
∴∠AOF=120°-∠BOF,∠BOG=∠DOE-∠BOF=120°-∠BOF,
∴∠AOF=∠BOG,
∴△AOF≌△BOG,
S四边形OFBG=S△OAB=S△ABC。
即扇形与△ABC的重叠部分的面积总等于△ABC的面积的。
由(1)(2)可知,当扇形的圆心角为120°时,△ABC与扇形重叠部分的面积总等于△ABC的面积的。
A
B
C
D
E
第7题
图②
图③
图①
A
F
B
E
C
D
O
·
模型甲
模型乙
A
D
E
O
B
x
y
·
C
A
B
C
D
F
E
D
M
·
A
O
B
C
D
E
O
C
A
B
A
F
B
E
C
D
O
·
A
D
E
O
B
x
y
·
C
A
B
C
D
E
F
E
D
M
·
A
O
B
C
D
E
O
C
A
B
F
G
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
