平行四边形判定(一)课件
文档属性
| 名称 | 平行四边形判定(一)课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-29 00:00:00 | ||
图片预览


文档简介
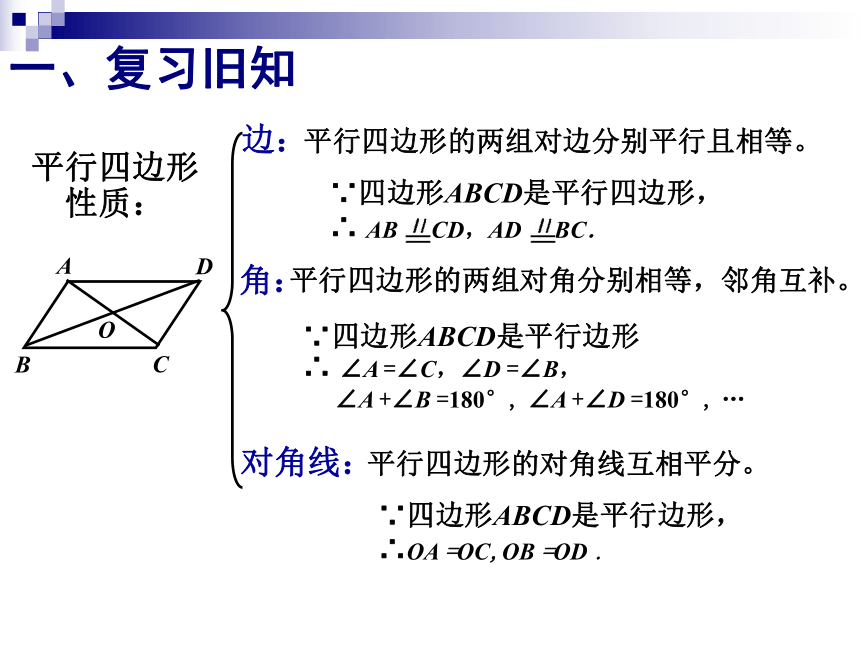
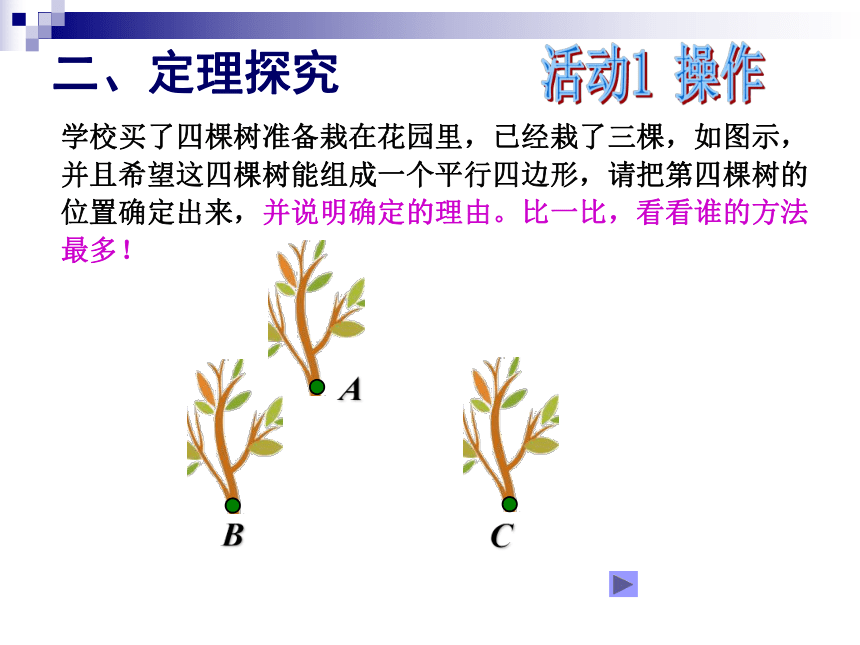
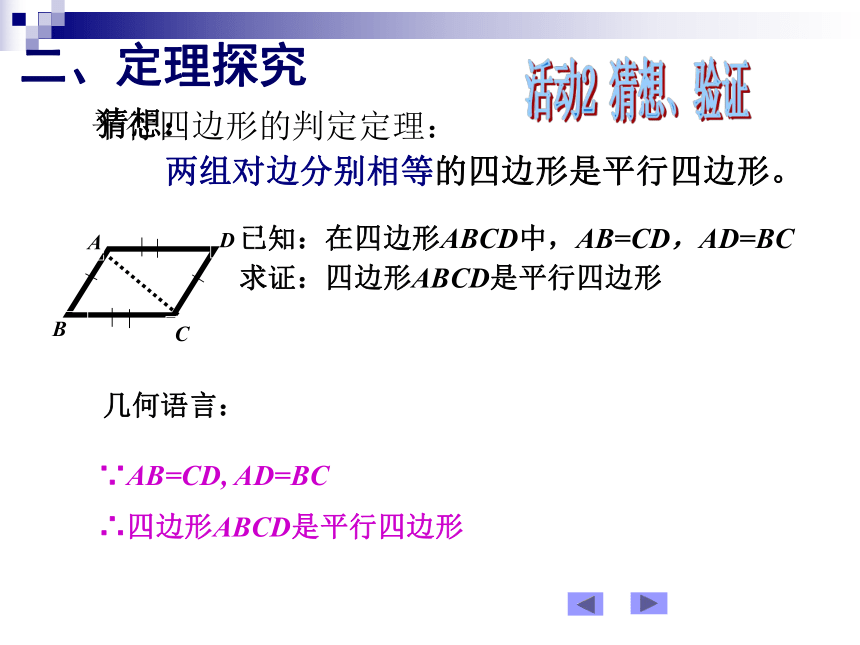
课件14张PPT。平行四边形的判定执教:中数组 汤秀芳(一) 两组对边分别相等的四边形是平行四边形。已知:在四边形ABCD中,AB=CD,AD=BC
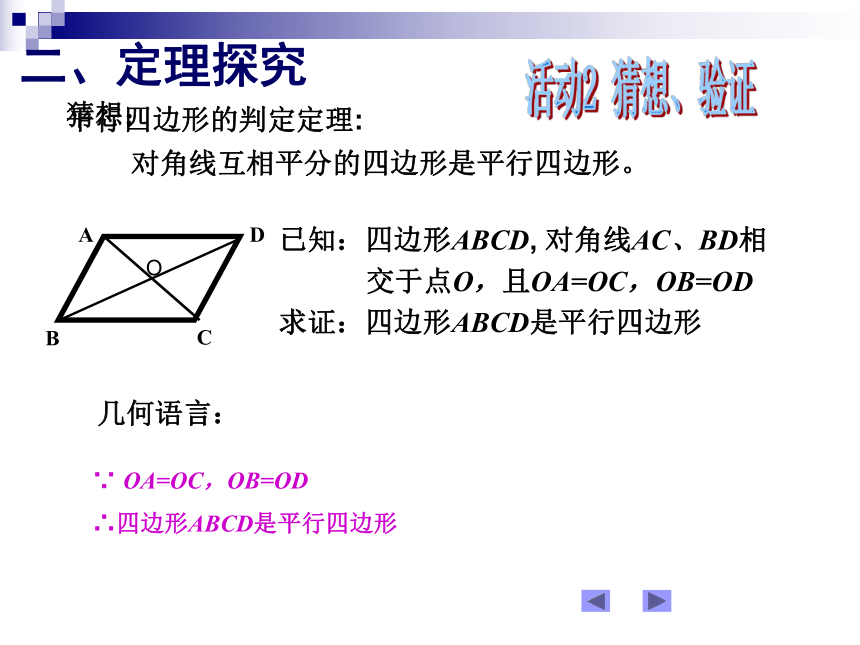
求证:四边形ABCD是平行四边形活动2 猜想、验证二、定理探究猜想:已知:四边形ABCD, 对角线AC、BD相
交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形二、定理探究猜想:
对角线互相平分的四边形是平行四边形。平行四边形的判定定理:
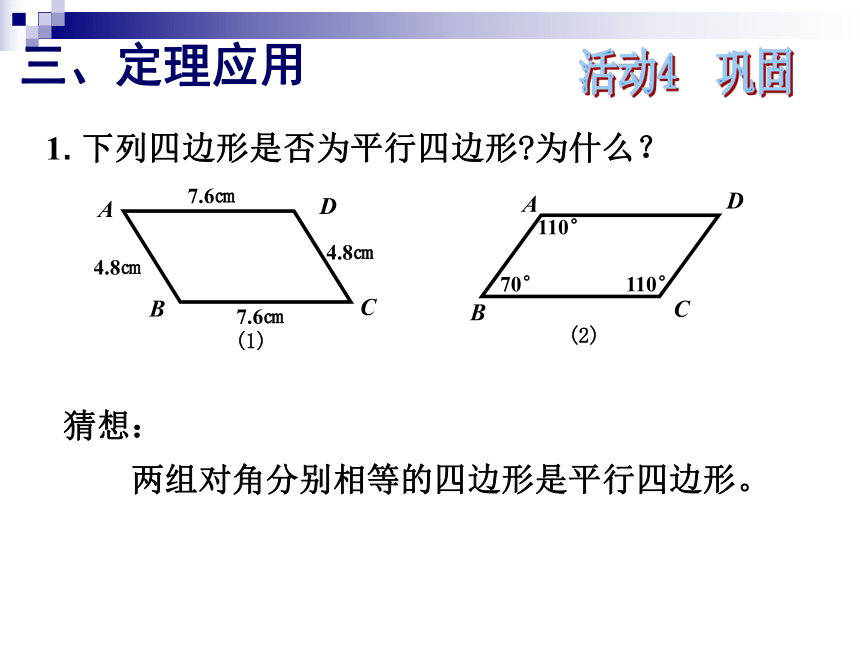
活动2 猜想、验证从边来判定两组对边分别平行的四边形是平行四边形。 两组对边分别相等的四边形是平行四边形。从角来判定两组对角分别相等的四边形是平行四边形。从对角线来判定对角线互相平分的四边形是平行四边形。平行四边形的判定方法:活动3 归纳二、定理探究一组对边平行且相等的四边形是平行四边形。1. 下列四边形是否为平行四边形?为什么?(1)(2)BADC4.8㎝4.8㎝7.6㎝7.6㎝活动4 巩固三、定理应用猜想: 两组对角分别相等的四边形是平行四边形。已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
几何语言
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形 两组对角分别相等的四边形是平行四边形。平行四边形的判定定理 :证明:∵ ∠A +∠B+∠C + ∠D =360°
∠A=∠C, ∠B =∠D
∴ 2 ∠A + 2 ∠B = 360°
∴ ∠A+∠B=180°
∴ AD∥BC
同理可证:∠B+∠C=180°
∴ AB∥CD
∴ 四边形ABCD是平行四边形。
验证猜想3. 选择: 下面给出了四边形ABCD中∠A、∠B、∠C、
∠D的度数之比,其中能判定四边形ABCD是
平行四边形的是( ) A.1:2:3:4 B.2:2:3:3 C.2:3:2:3 D.2:3:3:2C活动4 巩固三、定理应用2. 判断:一组对边平行,另一组对边相等的四边
形是平行四边形. ( )×一组对边平行,另一组对边相等的四边形是平行四边形或等腰梯形5. 变式训练: (1)在上题中,若E、F分别在对角线AC延长线上, 如图所示,其余条件不变,结论仍然成立吗? 若成立,请证明.DABCEF活动5 提升三、定理应用ADCBEFGHO活动5 提升三、定理应用5. 变式训练: (2)在上题中,若E、 F 、G、H分别是AO、BO、 CO、DO的中点,其它条件不变,请以图中的 点为顶点,尽可能多地画出平行四边形。1. 本节课你学会了几种平行四边形的判定方法?2. 本节课所学的解决问题的思路是: (2)平行四边形的问题常转化为三角形来解决.(1)探究数学问题,一般要经历“动手实践” →
“猜想” →“验证猜想(证明)” →“得出结
论”等过程。3. 数学思想:转化、类比活动6 小结三、回顾与反思欢迎批评指教谢谢大家!2011.03.18
求证:四边形ABCD是平行四边形活动2 猜想、验证二、定理探究猜想:已知:四边形ABCD, 对角线AC、BD相
交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形二、定理探究猜想:
对角线互相平分的四边形是平行四边形。平行四边形的判定定理:
活动2 猜想、验证从边来判定两组对边分别平行的四边形是平行四边形。 两组对边分别相等的四边形是平行四边形。从角来判定两组对角分别相等的四边形是平行四边形。从对角线来判定对角线互相平分的四边形是平行四边形。平行四边形的判定方法:活动3 归纳二、定理探究一组对边平行且相等的四边形是平行四边形。1. 下列四边形是否为平行四边形?为什么?(1)(2)BADC4.8㎝4.8㎝7.6㎝7.6㎝活动4 巩固三、定理应用猜想: 两组对角分别相等的四边形是平行四边形。已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
几何语言
∵∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形 两组对角分别相等的四边形是平行四边形。平行四边形的判定定理 :证明:∵ ∠A +∠B+∠C + ∠D =360°
∠A=∠C, ∠B =∠D
∴ 2 ∠A + 2 ∠B = 360°
∴ ∠A+∠B=180°
∴ AD∥BC
同理可证:∠B+∠C=180°
∴ AB∥CD
∴ 四边形ABCD是平行四边形。
验证猜想3. 选择: 下面给出了四边形ABCD中∠A、∠B、∠C、
∠D的度数之比,其中能判定四边形ABCD是
平行四边形的是( ) A.1:2:3:4 B.2:2:3:3 C.2:3:2:3 D.2:3:3:2C活动4 巩固三、定理应用2. 判断:一组对边平行,另一组对边相等的四边
形是平行四边形. ( )×一组对边平行,另一组对边相等的四边形是平行四边形或等腰梯形5. 变式训练: (1)在上题中,若E、F分别在对角线AC延长线上, 如图所示,其余条件不变,结论仍然成立吗? 若成立,请证明.DABCEF活动5 提升三、定理应用ADCBEFGHO活动5 提升三、定理应用5. 变式训练: (2)在上题中,若E、 F 、G、H分别是AO、BO、 CO、DO的中点,其它条件不变,请以图中的 点为顶点,尽可能多地画出平行四边形。1. 本节课你学会了几种平行四边形的判定方法?2. 本节课所学的解决问题的思路是: (2)平行四边形的问题常转化为三角形来解决.(1)探究数学问题,一般要经历“动手实践” →
“猜想” →“验证猜想(证明)” →“得出结
论”等过程。3. 数学思想:转化、类比活动6 小结三、回顾与反思欢迎批评指教谢谢大家!2011.03.18
