解直角三角形
图片预览






文档简介
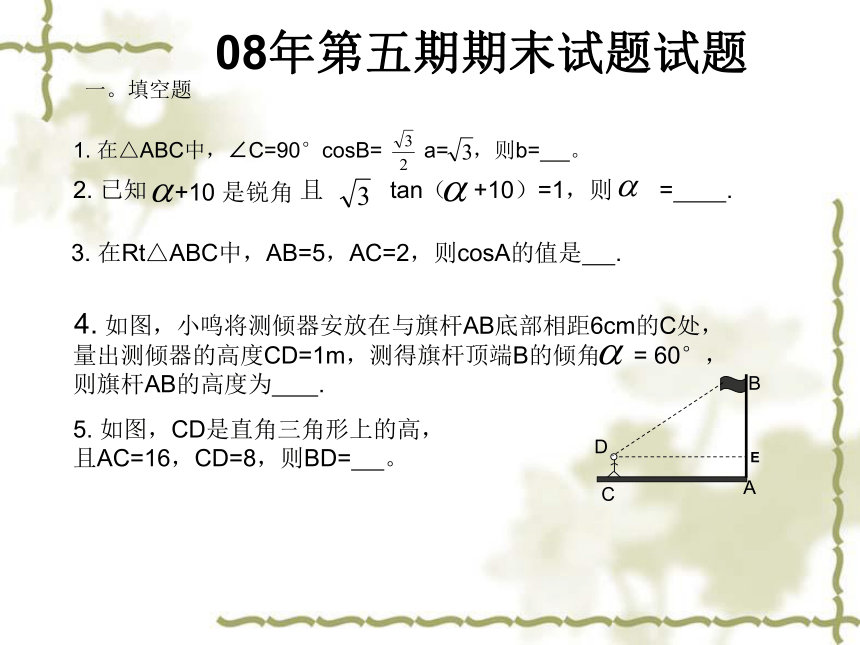
课件24张PPT。解直角三角形一.本节重点二.应用题型三.怎样强化解直角三角形一。填空题1. 在△ABC中,∠C=90°cosB= a= ,则b= 。2. 已知 且 tan( +10)=1,则 = .+10 是锐角 3. 在Rt△ABC中,AB=5,AC=2,则cosA的值是 . 4. 如图,小鸣将测倾器安放在与旗杆AB底部相距6cm的C处,
量出测倾器的高度CD=1m,测得旗杆顶端B的倾角 = 60°,
则旗杆AB的高度为 .5. 如图,CD是直角三角形上的高,
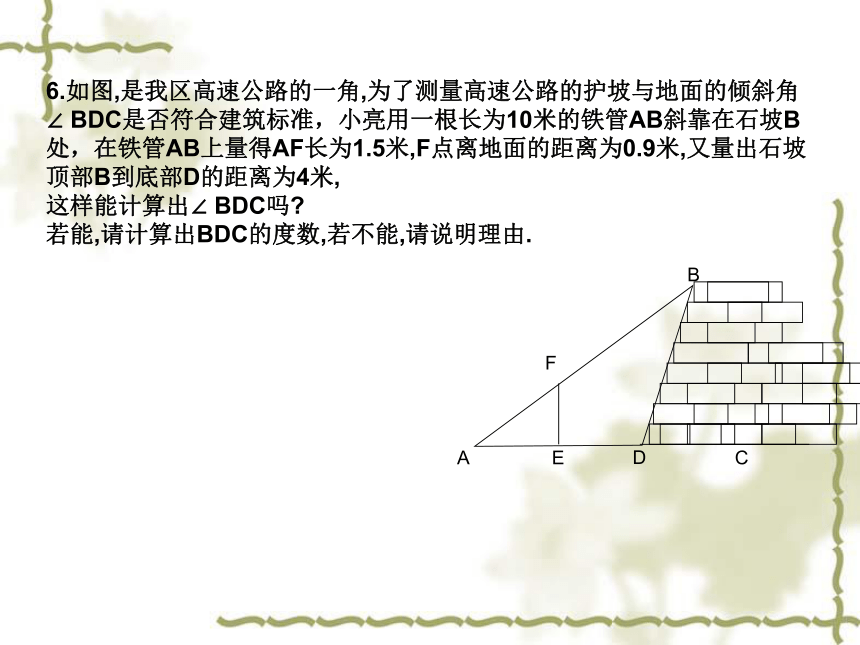
且AC=16,CD=8,则BD= 。08年第五期期末试题试题6.如图,是我区高速公路的一角,为了测量高速公路的护坡与地面的倾斜角
∠ BDC是否符合建筑标准,小亮用一根长为10米的铁管AB斜靠在石坡B
处,在铁管AB上量得AF长为1.5米,F点离地面的距离为0.9米,又量出石坡
顶部B到底部D的距离为4米,
这样能计算出∠ BDC吗?
若能,请计算出BDC的度数,若不能,请说明理由.ADBFEC09年第五期期末试题试题1.计算:
2.如图,在△ABC中,∠C=90°,BC=6,AC=8,则cosA等于 .
3.如图,CD是直角三角形斜边上的高,且AC=16,CD=8,则BD= .
4.如图,为了测量河岸A,B两点距离,在与AB垂直的方向取点C,
测量AC=20米, ∠ACB,则AB= 米.
5.如图,CD是一平面镜,光线从A点出发经CD上点E反射到B点,若入射
角为X(入射角等于反射角),AC ⊥ CD,BDCD,垂足分别为C,D,且AC=3
BD=6,CD=11,则tanx的值为 .
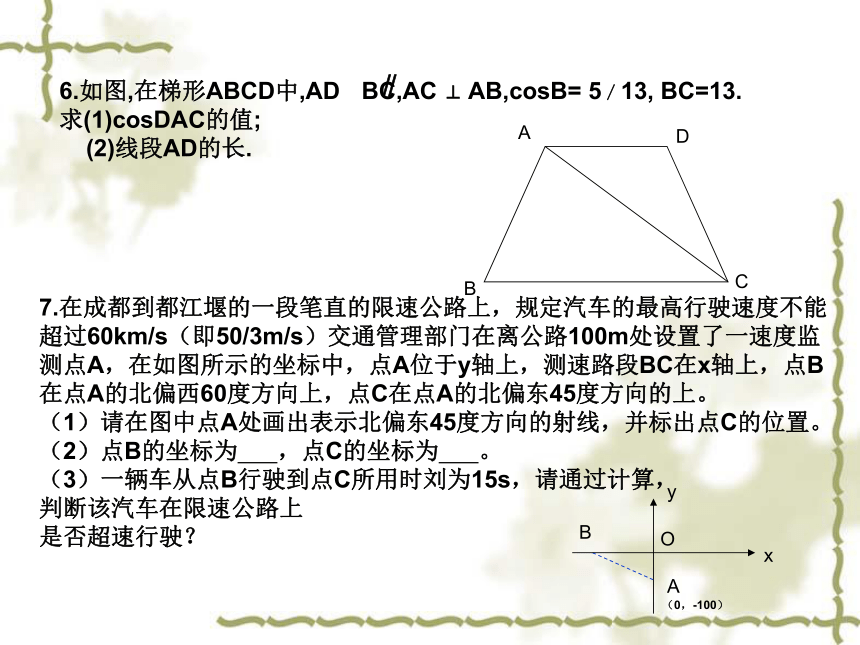
ABDCExx6.如图,在梯形ABCD中,AD BC,AC ⊥ AB,cosB= 5/13, BC=13.
求(1)cosDAC的值;
(2)线段AD的长.∥C7.在成都到都江堰的一段笔直的限速公路上,规定汽车的最高行驶速度不能
超过60km/s(即50/3m/s)交通管理部门在离公路100m处设置了一速度监
测点A,在如图所示的坐标中,点A位于y轴上,测速路段BC在x轴上,点B
在点A的北偏西60度方向上,点C在点A的北偏东45度方向的上。
(1)请在图中点A处画出表示北偏东45度方向的射线,并标出点C的位置。
(2)点B的坐标为 ,点C的坐标为 。
(3)一辆车从点B行驶到点C所用时刘为15s,请通过计算,
判断该汽车在限速公路上
是否超速行驶?(0,-100)1.如图,在Rt△ABC 中 是斜边上的中线,已知
则 的值是( )
2. 菱形在平面直角坐标系中的位置如图所示,
则点B的坐标为 .
3.如图,在 中, 且 ,那么BC= .10年第五期期末试题试题4 .计算题: 6.某中学九年级学生在学习“解直角三角形”一章时,
开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度.
如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,
然后向教学楼前进60米到达点D,又测得点A的仰角为45°.
请你根据这些数据,求出这幢教学楼的高度.(计算过程和结果均不取近似值)5.如图, ,点P是 的角平分线上一点,过点P作 交BO于C,
若0C=4,则点P到OA的距离PD( ) A一.近三年情况分析1.已知角,求值
2.已知值,求角
3. 确定值、角的范围
已知 tanA= ,求锐角A .
在Rt△ABC中∠C=90°,当 锐角A>45°时,
sinA的取值范围( )
4 .在方格纸中求三角函数值在正方形网格中,点A、B、C、D的位置如图所示,
则cosB的值为( )5。等角的三角函数值转化已知如图,在Rt△ABC中,CD ⊥ AB,
AC= 3 ,BC=2,那么sin ∠ ACD=强化知识点:?在△ABC中,若 ,
则∠C= . 6。非负数与三角函数值的套用7。坡度问题三.如何复习!一。锐角三角函数二。解直角三角形
知识结构
第一节课:
锐角三角函数 第二节课:
解直角三角形解直角三角形第一课时:锐角三角函数目的:夯实基础,三角函数有关公式的灵活转化,解决疑难。方式:接龙,竞赛活动,探究方式具体安排:
1。回顾特殊三角函数值表,
2。根据表格内容复习函数的增减性,
同角函数关系,互为余角间的函数转化。
3。定时小测验。
4。疑难解答。内容:1.锐角三角函数的有关概念;
2.特殊角三角函数值
3.锐角三角函数运用特殊角的三角函数值1、2、直角三角形的边角关系
在Rt△ABC中,∠C=90°,分别是∠A,∠B,∠C的对边,则
(1)三边之间的关系:;(勾股定理)
(2)锐角之间的关系:∠A+∠B= ;
(3)锐角三角函数的定义:
3、锐角三角函数的有关性质
(1)当0°<A<90°时, <sinA< , <cosA< ,
tanA> , cotA> .
(2)在0°~90°之间,正弦(或正切)值随角度的增大而 ,随角度的减小而 ;
余弦(余切)值随角度的增大而 ,随角度的减小而 .
(3)同角三角函数的关系:
sin2A+ cos2A= , tanA·cotA=
(4)正弦(切)与余弦(切)的转换关系:
sinA=cos( ), cosA=sin( ) ,
tanA=cot( ), cotA=tan( )
(5)直角三角形中,30°所对的直角边等于斜边的 .
(6)直角三角形中,斜边上的中线等于斜边的 .10分钟小测验
6。如图,在矩形ABCD中,DE⊥AC于E,设∠ADE= ,且cos= ,AB=4,
则AD的长为 .2、在Rt△ABC中,∠C=90°,如果cosA= ,那么tanB的值为 。
5。在Rt△ABC中,CD为斜边AB上的高,且AD=4,BD=2,那么tanA等于 1。在Rt△ABC中, ∠C=90° ∠B=50°,AB=10,则BC的长为 ?3.比较大小sin 20° cos 40°,tan 55° cot 75°4。锐角A满足2sin(A—15°)= ,则∠ A=一题多解已知在方格纸中,求∠1 + ∠2 + ∠3=?
第二课时:解直角三角形应用目的:1.通过复习,提练解直角三角形与方程之间的关系
2通过练习,使学生能提练出解直角三角
形的两个基本图。让学生把实际问题转化为数学
问题的思想 ,数形结合的思想
3.归纳出解直角三角形的意义,类型和相应的解法。内容:1.解直角三角形的概念
2.仰角和俯角,方位角,坡度的概念
3.解直角三角形的实际应用
具体安排:1、解直角三角形的基本类型及其解法总结:2、解直角三角形的应用概念反馈(1)仰角和俯角(2)方位角
(3)坡度两个基本图形例1。
小明在距白塔AD100米外的点B测得塔顶的仰角为60度,
则该AD塔的高度为( )例2。
如图,小明先在点B测得白塔AD的顶点A的仰角为30°,
然后向白塔前进60米到达点C,又测得点A的仰角为45°,
请你根据这些数据,求出这座白塔的高度。ADB典例赏析例3.如图,海岛A四周20海里周围内为暗礁区,
一艘货轮由东向西航行,在B处见岛A在北偏西60?,
航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,
有无触礁的危险?例4、如图所示,B、C是河对岸的两点,A是对岸岸边一点,测量∠ABC=45°,
∠ACB=30°,BC=60米,则点A到BC的距离是 米。
(精确到0.01米)
例5、如图,拦水坝的横截面是梯形ABCD,
已知坝高为4米,坝顶宽AD为3米,
背水坡AB的坡度i=1:3,
迎水坡CD长为5米.
(1)求大坝的下底宽CD的长;
(2)修建这种大坝100米,需要多少土石方?谢谢,再见!
量出测倾器的高度CD=1m,测得旗杆顶端B的倾角 = 60°,
则旗杆AB的高度为 .5. 如图,CD是直角三角形上的高,
且AC=16,CD=8,则BD= 。08年第五期期末试题试题6.如图,是我区高速公路的一角,为了测量高速公路的护坡与地面的倾斜角
∠ BDC是否符合建筑标准,小亮用一根长为10米的铁管AB斜靠在石坡B
处,在铁管AB上量得AF长为1.5米,F点离地面的距离为0.9米,又量出石坡
顶部B到底部D的距离为4米,
这样能计算出∠ BDC吗?
若能,请计算出BDC的度数,若不能,请说明理由.ADBFEC09年第五期期末试题试题1.计算:
2.如图,在△ABC中,∠C=90°,BC=6,AC=8,则cosA等于 .
3.如图,CD是直角三角形斜边上的高,且AC=16,CD=8,则BD= .
4.如图,为了测量河岸A,B两点距离,在与AB垂直的方向取点C,
测量AC=20米, ∠ACB,则AB= 米.
5.如图,CD是一平面镜,光线从A点出发经CD上点E反射到B点,若入射
角为X(入射角等于反射角),AC ⊥ CD,BDCD,垂足分别为C,D,且AC=3
BD=6,CD=11,则tanx的值为 .
ABDCExx6.如图,在梯形ABCD中,AD BC,AC ⊥ AB,cosB= 5/13, BC=13.
求(1)cosDAC的值;
(2)线段AD的长.∥C7.在成都到都江堰的一段笔直的限速公路上,规定汽车的最高行驶速度不能
超过60km/s(即50/3m/s)交通管理部门在离公路100m处设置了一速度监
测点A,在如图所示的坐标中,点A位于y轴上,测速路段BC在x轴上,点B
在点A的北偏西60度方向上,点C在点A的北偏东45度方向的上。
(1)请在图中点A处画出表示北偏东45度方向的射线,并标出点C的位置。
(2)点B的坐标为 ,点C的坐标为 。
(3)一辆车从点B行驶到点C所用时刘为15s,请通过计算,
判断该汽车在限速公路上
是否超速行驶?(0,-100)1.如图,在Rt△ABC 中 是斜边上的中线,已知
则 的值是( )
2. 菱形在平面直角坐标系中的位置如图所示,
则点B的坐标为 .
3.如图,在 中, 且 ,那么BC= .10年第五期期末试题试题4 .计算题: 6.某中学九年级学生在学习“解直角三角形”一章时,
开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度.
如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,
然后向教学楼前进60米到达点D,又测得点A的仰角为45°.
请你根据这些数据,求出这幢教学楼的高度.(计算过程和结果均不取近似值)5.如图, ,点P是 的角平分线上一点,过点P作 交BO于C,
若0C=4,则点P到OA的距离PD( ) A一.近三年情况分析1.已知角,求值
2.已知值,求角
3. 确定值、角的范围
已知 tanA= ,求锐角A .
在Rt△ABC中∠C=90°,当 锐角A>45°时,
sinA的取值范围( )
4 .在方格纸中求三角函数值在正方形网格中,点A、B、C、D的位置如图所示,
则cosB的值为( )5。等角的三角函数值转化已知如图,在Rt△ABC中,CD ⊥ AB,
AC= 3 ,BC=2,那么sin ∠ ACD=强化知识点:?在△ABC中,若 ,
则∠C= . 6。非负数与三角函数值的套用7。坡度问题三.如何复习!一。锐角三角函数二。解直角三角形
知识结构
第一节课:
锐角三角函数 第二节课:
解直角三角形解直角三角形第一课时:锐角三角函数目的:夯实基础,三角函数有关公式的灵活转化,解决疑难。方式:接龙,竞赛活动,探究方式具体安排:
1。回顾特殊三角函数值表,
2。根据表格内容复习函数的增减性,
同角函数关系,互为余角间的函数转化。
3。定时小测验。
4。疑难解答。内容:1.锐角三角函数的有关概念;
2.特殊角三角函数值
3.锐角三角函数运用特殊角的三角函数值1、2、直角三角形的边角关系
在Rt△ABC中,∠C=90°,分别是∠A,∠B,∠C的对边,则
(1)三边之间的关系:;(勾股定理)
(2)锐角之间的关系:∠A+∠B= ;
(3)锐角三角函数的定义:
3、锐角三角函数的有关性质
(1)当0°<A<90°时, <sinA< , <cosA< ,
tanA> , cotA> .
(2)在0°~90°之间,正弦(或正切)值随角度的增大而 ,随角度的减小而 ;
余弦(余切)值随角度的增大而 ,随角度的减小而 .
(3)同角三角函数的关系:
sin2A+ cos2A= , tanA·cotA=
(4)正弦(切)与余弦(切)的转换关系:
sinA=cos( ), cosA=sin( ) ,
tanA=cot( ), cotA=tan( )
(5)直角三角形中,30°所对的直角边等于斜边的 .
(6)直角三角形中,斜边上的中线等于斜边的 .10分钟小测验
6。如图,在矩形ABCD中,DE⊥AC于E,设∠ADE= ,且cos= ,AB=4,
则AD的长为 .2、在Rt△ABC中,∠C=90°,如果cosA= ,那么tanB的值为 。
5。在Rt△ABC中,CD为斜边AB上的高,且AD=4,BD=2,那么tanA等于 1。在Rt△ABC中, ∠C=90° ∠B=50°,AB=10,则BC的长为 ?3.比较大小sin 20° cos 40°,tan 55° cot 75°4。锐角A满足2sin(A—15°)= ,则∠ A=一题多解已知在方格纸中,求∠1 + ∠2 + ∠3=?
第二课时:解直角三角形应用目的:1.通过复习,提练解直角三角形与方程之间的关系
2通过练习,使学生能提练出解直角三角
形的两个基本图。让学生把实际问题转化为数学
问题的思想 ,数形结合的思想
3.归纳出解直角三角形的意义,类型和相应的解法。内容:1.解直角三角形的概念
2.仰角和俯角,方位角,坡度的概念
3.解直角三角形的实际应用
具体安排:1、解直角三角形的基本类型及其解法总结:2、解直角三角形的应用概念反馈(1)仰角和俯角(2)方位角
(3)坡度两个基本图形例1。
小明在距白塔AD100米外的点B测得塔顶的仰角为60度,
则该AD塔的高度为( )例2。
如图,小明先在点B测得白塔AD的顶点A的仰角为30°,
然后向白塔前进60米到达点C,又测得点A的仰角为45°,
请你根据这些数据,求出这座白塔的高度。ADB典例赏析例3.如图,海岛A四周20海里周围内为暗礁区,
一艘货轮由东向西航行,在B处见岛A在北偏西60?,
航行24海里到C,见岛A在北偏西30?,货轮继续向西航行,
有无触礁的危险?例4、如图所示,B、C是河对岸的两点,A是对岸岸边一点,测量∠ABC=45°,
∠ACB=30°,BC=60米,则点A到BC的距离是 米。
(精确到0.01米)
例5、如图,拦水坝的横截面是梯形ABCD,
已知坝高为4米,坝顶宽AD为3米,
背水坡AB的坡度i=1:3,
迎水坡CD长为5米.
(1)求大坝的下底宽CD的长;
(2)修建这种大坝100米,需要多少土石方?谢谢,再见!
