弧度制课件
图片预览










文档简介
课件54张PPT。一、阅读教材P6~8回答
1.弧度制的概念
(1)定义
我们把弧长等于 长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作 .
用弧度作为单位来度量角的制度叫做 .
用弧度制表示角的时候,“弧度”或“rad”经常省略,即只写一实数表示角的度量,但以角度制表示角时,单位不能省略.半径弧度弧度制(2)我们知道,角有正、负、零角之分,它的弧度数也应该有正、负、零之分,由角的旋转方向决定.一般地,正角的弧度数为 ,负角的弧度数为 ,零角的弧度数为 .正数负数零
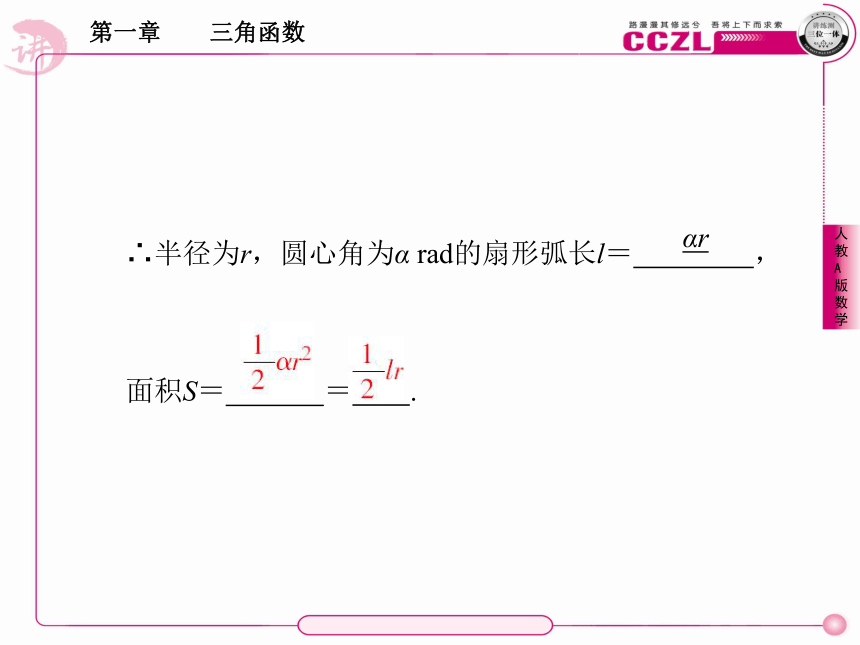
∴半径为r,圆心角为α rad的扇形弧长l= ,
面积S= = .αr3.角度与弧度的换算
180°= rad.
1°= rad≈0.01745rad,
1rad=( )°≈57.30°.
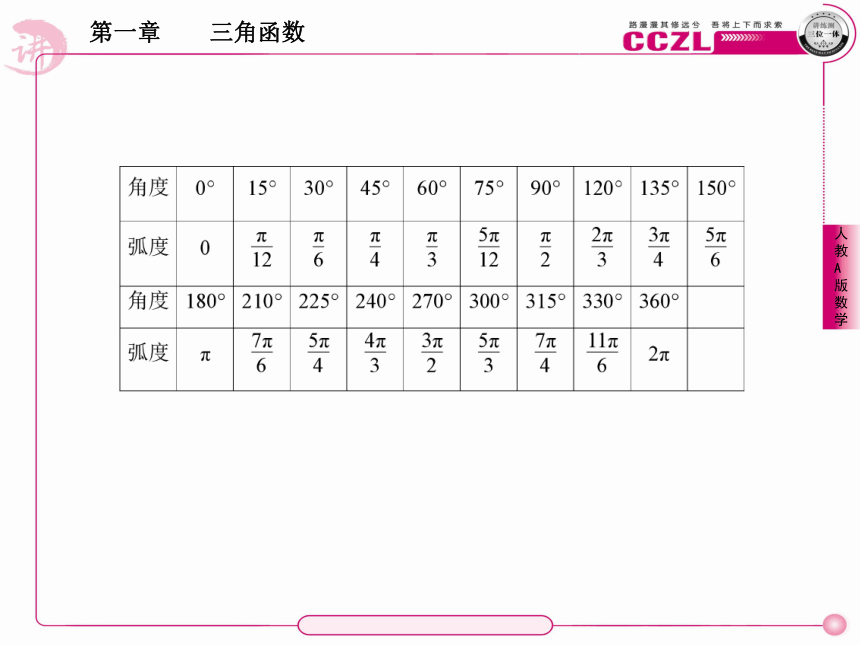
角度与弧度的换算要熟练掌握,见下表.π重点:弧度的概念,角度与弧度的互化,弧长公式.
难点:角度与弧度互化和公式的应用.1.对概念的理解
关于弧度的理解,主要明确以下几点:
(1)和角度制对比,弧度制是以“弧度”为单位来度量角的单位制,而角度制是以“度”为单位来度量角的单位制.(2)在弧度制中,角的弧度数表示弧长与半径的比值,是一个实数.建立弧度制后,在角的集合与实数集R之间建立了一一对应的关系.即:每一个角都有惟一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有惟一的一个角(角的弧度数等于这个实数)与它对应.
2.角度制与弧度制的互化要牢记π rad=180°.[分析] 角度与弧度的互化要抓住π rad=180°.
[例2] 如图所示.
(1)分别写出终边落在OA,OB位置上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.(2)角的终边为实线时表示包括该角,为虚线时不包括该角.
如图,用弧度制表示顶点在原点,始边与x轴的非负半轴重合,终边落在阴影部分的角的集合(不包括边界).
[例3] 已知扇形的面积为S,当扇形的中心角为多少弧度时,扇形的周长最小?并求出此最小值.
[分析] 欲求周长C的最小值,以扇形的半径r为自变量确定函数关系,转化为求函数最值.
已知一扇形的周长为c(c>0),当扇形的圆心角为何值时,它的面积最大?求出面积的最大值?[辨析] 错解对集合的概念不理解,认为两个集合中的k取同一个值时找M与P的对应元素.[答案] B[答案] D[答案] A[答案] C[答案] A7.在直径为10cm的轮上,有一长为6cm的弦,P为该弦的中点,轮子以每秒5弧度的角速度旋转,则经过5秒钟后点P转过的弧长是________.
[答案] 100cm
[解析] 即以4cm为半径,圆心角为25弧度的弧长,由弧长公式知,该弧长为100cm.8.(用弧度制表示)第一象限角的集合为__________,第一或第三象限角的集合为__________.终边落在x轴上的角的集合为________,终边落在坐标轴上的角的集合为________,终边落在直线y=-x上的角的集合为________.三、解答题
9.(1)已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.
(2)已知扇形周长为20 cm,当扇形的中心角为多大时它有最大面积?
1.弧度制的概念
(1)定义
我们把弧长等于 长的弧所对的圆心角叫做1弧度的角,用符号rad表示,读作 .
用弧度作为单位来度量角的制度叫做 .
用弧度制表示角的时候,“弧度”或“rad”经常省略,即只写一实数表示角的度量,但以角度制表示角时,单位不能省略.半径弧度弧度制(2)我们知道,角有正、负、零角之分,它的弧度数也应该有正、负、零之分,由角的旋转方向决定.一般地,正角的弧度数为 ,负角的弧度数为 ,零角的弧度数为 .正数负数零
∴半径为r,圆心角为α rad的扇形弧长l= ,
面积S= = .αr3.角度与弧度的换算
180°= rad.
1°= rad≈0.01745rad,
1rad=( )°≈57.30°.
角度与弧度的换算要熟练掌握,见下表.π重点:弧度的概念,角度与弧度的互化,弧长公式.
难点:角度与弧度互化和公式的应用.1.对概念的理解
关于弧度的理解,主要明确以下几点:
(1)和角度制对比,弧度制是以“弧度”为单位来度量角的单位制,而角度制是以“度”为单位来度量角的单位制.(2)在弧度制中,角的弧度数表示弧长与半径的比值,是一个实数.建立弧度制后,在角的集合与实数集R之间建立了一一对应的关系.即:每一个角都有惟一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有惟一的一个角(角的弧度数等于这个实数)与它对应.
2.角度制与弧度制的互化要牢记π rad=180°.[分析] 角度与弧度的互化要抓住π rad=180°.
[例2] 如图所示.
(1)分别写出终边落在OA,OB位置上的角的集合;
(2)写出终边落在阴影部分(包括边界)的角的集合.(2)角的终边为实线时表示包括该角,为虚线时不包括该角.
如图,用弧度制表示顶点在原点,始边与x轴的非负半轴重合,终边落在阴影部分的角的集合(不包括边界).
[例3] 已知扇形的面积为S,当扇形的中心角为多少弧度时,扇形的周长最小?并求出此最小值.
[分析] 欲求周长C的最小值,以扇形的半径r为自变量确定函数关系,转化为求函数最值.
已知一扇形的周长为c(c>0),当扇形的圆心角为何值时,它的面积最大?求出面积的最大值?[辨析] 错解对集合的概念不理解,认为两个集合中的k取同一个值时找M与P的对应元素.[答案] B[答案] D[答案] A[答案] C[答案] A7.在直径为10cm的轮上,有一长为6cm的弦,P为该弦的中点,轮子以每秒5弧度的角速度旋转,则经过5秒钟后点P转过的弧长是________.
[答案] 100cm
[解析] 即以4cm为半径,圆心角为25弧度的弧长,由弧长公式知,该弧长为100cm.8.(用弧度制表示)第一象限角的集合为__________,第一或第三象限角的集合为__________.终边落在x轴上的角的集合为________,终边落在坐标轴上的角的集合为________,终边落在直线y=-x上的角的集合为________.三、解答题
9.(1)已知扇形OAB的圆心角α为120°,半径为6,求扇形弧长及所含弓形的面积.
(2)已知扇形周长为20 cm,当扇形的中心角为多大时它有最大面积?
