1.2 任意角的三角函数
图片预览








文档简介
课件68张PPT。1.2 任意角的三角函数一、阅读教材P11~14回答
1.单位圆的定义:在直角坐标系中,我们称以 为圆心,以 为半径的圆为单位圆.
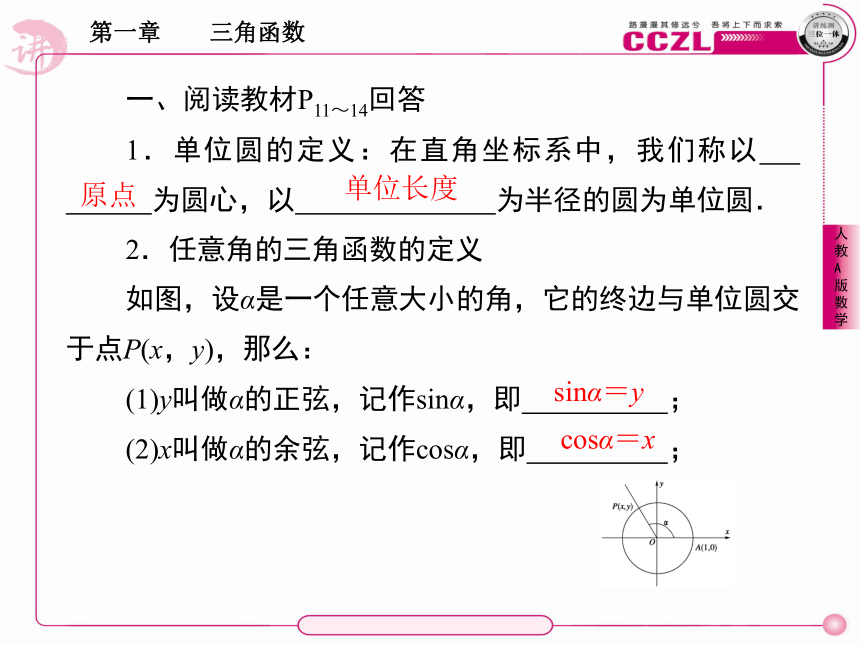
2.任意角的三角函数的定义
如图,设α是一个任意大小的角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的正弦,记作sinα,即 ;
(2)x叫做α的余弦,记作cosα,即 ;原点单位长度sinα=ycosα=x(3) 叫做α的正切,记作tanα,即 .
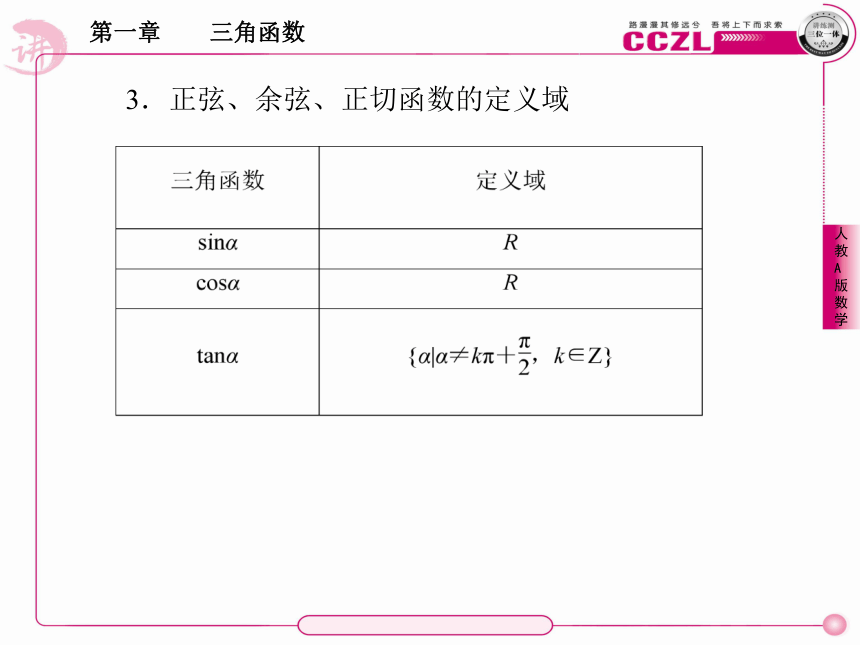
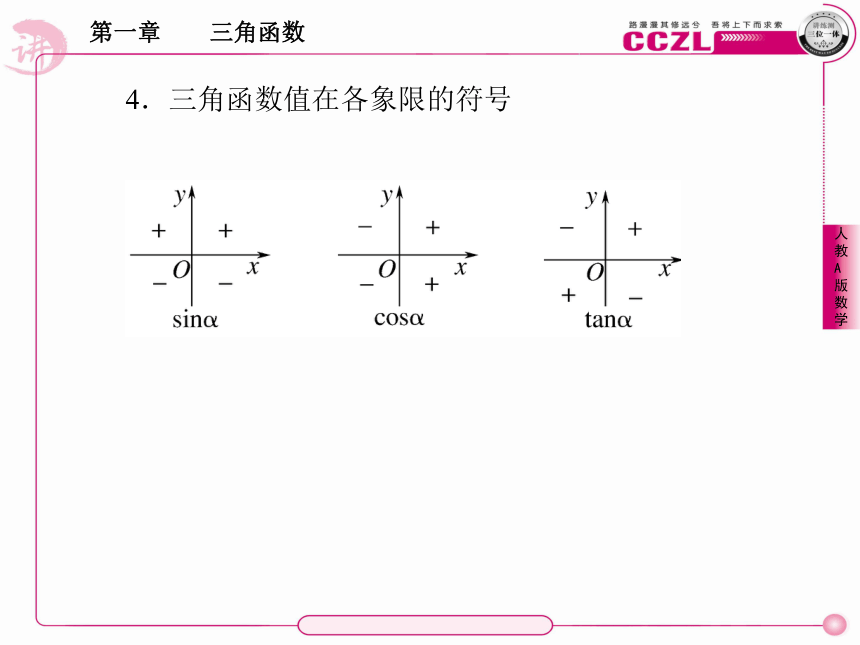
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或比值为函数值的函数,我们将它们统称为三角函数.由于角的集合与实数之间可以建立一一对应关系,三角函数可以看成自变量为 的函数.实数3.正弦、余弦、正切函数的定义域4.三角函数值在各象限的符号5.诱导公式(一)
根据三角函数的定义可以知道,终边相同的角的同名三角函数的值 .
由此得到诱导公式(一).
sin(α+k·2π)= ,
cos(α+k·2π)= ,
tan(α+k·2π)= .
其中k∈Z.相等sinαcosαtanα二、解答下列问题
1.sin0= ,cosπ= ,sin = , tan
= .
2.(1)如果sinα>0,且cosα<0,则α是第 象限的角;
(2)如果tanα>0,且cosα<0,则α是第 象限的角;
(3)如果sinα<0,且tanα<0,则α是第 象限的角;
(4)如果cosα>0,且sinα<0,则α是第 象限的角.0-1-1不存在二三四四重点:①任意角三角函数的定义与正弦、余弦、正切函数的定义域.
②三角函数值的符号的判定和诱导公式(一).
难点:①根据三角函数的定义求三角函数值.
②正切函数定义域.1.对三角函数定义的理解
(1)各三角函数都是以实数为自变量,以比值为函数值的函数,其关系如下图所示.
这样,三角函数就像前面研究的其它基本初等函数一样,都是以实数为自变量的函数了.2.各象限三角函数值的符号可只记忆正的:“一全正,二正弦,三正切,四余弦”.
3.相等的角终边一定相同,但终边相同的角却不一定相等,终边相同的角有无数个,它们之间相差360°的整数倍.
在三角函数中,角和三角函数值的对应关系是多对一,即给定一个角,它的各个三角函数值是惟一确定的(不存在的情况除外);反过来,给定一个三角函数值,有无穷多个角和它对应,如:α=0时,sinα=0,但当sinα=0时,α=kπ,k∈Z.4.判断三角函数值的符号时,应特别注意角所在象限的确定,不要忽略终边落在坐标轴上的情况.
5.要重视单位圆在理解三角函数定义、定义域及三角函数值的符号中的作用.由于P(x,y)是角α的终边与单位圆的交点,∴当点P落在x轴上时sinα=0,tanα=0,cosα=±1,当点P落在y轴上时,cosα=0,tanα无意义,sinα=±1.当点P落在第二象限时,x<0,y>0,∴cosα<0,sinα>0,tanα<0等等.当角的终边相同时,点P的坐标相同,从而各三角函数值对应相等.这就是诱导公式(一).
[例1] 已知角α的终边经过点P(2,-3),求sinα,cosα,tanα的值.[点评] 本题易错点是开方时,忽视x的符号讨论,得出r=2x致误.
[分析] 计算r时,由于含有cosθ,应据角θ的象限确定cosθ的符号,再求r.[点评] 根据三角函数定义的要求,在角α终边上任取一点P(x,y),应有r=|OP|>0,故P与原点不重合;求已知角的三角函数值时,先在角的终边上取点P(x,y)探求x、y与r的关系,然后据定义求三角函数值.[答案] (1)< (2)< (3)<[分析] 先把角α表达成α=k·360°+β k∈Z,0°≤β<360°或α=2kπ+β k∈Z,0≤β<2π的形式,再套用诱导公式,然后结合象限定符号.选择题
1.若三角形的两内角α、β满足sinαcosβ<0,则此三角形必为
( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上三种情况都有可能[答案] B
[解析] ∵sinαcosβ<0,∴cosβ<0,
∴β是钝角,故选B.2.若角α的终边过点(-3,-2),则( )
A.sinαtanα>0 B.cosαtanα>0
C.sinαcosα>0 D.sinαcosα<0
[答案] C
[解析] ∵角α的终边过点(-3,-2),
∴sinα<0,cosα<0,tanα>0,
∴sinαcosα>0,故选C.3.角α满足条件sinα·cosα>0,sinα+cosα<0,则α在
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[答案] C
[解析] ∵sinαcosα>0,sinα+cosα<0
∴sinα<0,cosα<0,∴α是第三象限角.[答案] B[答案] B[答案] D7.(2010·深圳中学)若sin2α>0且cosα<0,则α是
( )
A.第二象限角
B.第一或第三象限角
C.第三象限角
D.第二或第三象限角
[答案] C[点评] 要熟记三角函数值的符号与角终边位置的关系.[答案] B
[解析] 当θ在第一象限时,sinθ>0,cosθ>0,tanθ>0,排除A、D;当θ在第四象限时,sinθ<0,cosθ>0,tanθ<0,排除C,故选B.
1.单位圆的定义:在直角坐标系中,我们称以 为圆心,以 为半径的圆为单位圆.
2.任意角的三角函数的定义
如图,设α是一个任意大小的角,它的终边与单位圆交于点P(x,y),那么:
(1)y叫做α的正弦,记作sinα,即 ;
(2)x叫做α的余弦,记作cosα,即 ;原点单位长度sinα=ycosα=x(3) 叫做α的正切,记作tanα,即 .
正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或比值为函数值的函数,我们将它们统称为三角函数.由于角的集合与实数之间可以建立一一对应关系,三角函数可以看成自变量为 的函数.实数3.正弦、余弦、正切函数的定义域4.三角函数值在各象限的符号5.诱导公式(一)
根据三角函数的定义可以知道,终边相同的角的同名三角函数的值 .
由此得到诱导公式(一).
sin(α+k·2π)= ,
cos(α+k·2π)= ,
tan(α+k·2π)= .
其中k∈Z.相等sinαcosαtanα二、解答下列问题
1.sin0= ,cosπ= ,sin = , tan
= .
2.(1)如果sinα>0,且cosα<0,则α是第 象限的角;
(2)如果tanα>0,且cosα<0,则α是第 象限的角;
(3)如果sinα<0,且tanα<0,则α是第 象限的角;
(4)如果cosα>0,且sinα<0,则α是第 象限的角.0-1-1不存在二三四四重点:①任意角三角函数的定义与正弦、余弦、正切函数的定义域.
②三角函数值的符号的判定和诱导公式(一).
难点:①根据三角函数的定义求三角函数值.
②正切函数定义域.1.对三角函数定义的理解
(1)各三角函数都是以实数为自变量,以比值为函数值的函数,其关系如下图所示.
这样,三角函数就像前面研究的其它基本初等函数一样,都是以实数为自变量的函数了.2.各象限三角函数值的符号可只记忆正的:“一全正,二正弦,三正切,四余弦”.
3.相等的角终边一定相同,但终边相同的角却不一定相等,终边相同的角有无数个,它们之间相差360°的整数倍.
在三角函数中,角和三角函数值的对应关系是多对一,即给定一个角,它的各个三角函数值是惟一确定的(不存在的情况除外);反过来,给定一个三角函数值,有无穷多个角和它对应,如:α=0时,sinα=0,但当sinα=0时,α=kπ,k∈Z.4.判断三角函数值的符号时,应特别注意角所在象限的确定,不要忽略终边落在坐标轴上的情况.
5.要重视单位圆在理解三角函数定义、定义域及三角函数值的符号中的作用.由于P(x,y)是角α的终边与单位圆的交点,∴当点P落在x轴上时sinα=0,tanα=0,cosα=±1,当点P落在y轴上时,cosα=0,tanα无意义,sinα=±1.当点P落在第二象限时,x<0,y>0,∴cosα<0,sinα>0,tanα<0等等.当角的终边相同时,点P的坐标相同,从而各三角函数值对应相等.这就是诱导公式(一).
[例1] 已知角α的终边经过点P(2,-3),求sinα,cosα,tanα的值.[点评] 本题易错点是开方时,忽视x的符号讨论,得出r=2x致误.
[分析] 计算r时,由于含有cosθ,应据角θ的象限确定cosθ的符号,再求r.[点评] 根据三角函数定义的要求,在角α终边上任取一点P(x,y),应有r=|OP|>0,故P与原点不重合;求已知角的三角函数值时,先在角的终边上取点P(x,y)探求x、y与r的关系,然后据定义求三角函数值.[答案] (1)< (2)< (3)<[分析] 先把角α表达成α=k·360°+β k∈Z,0°≤β<360°或α=2kπ+β k∈Z,0≤β<2π的形式,再套用诱导公式,然后结合象限定符号.选择题
1.若三角形的两内角α、β满足sinαcosβ<0,则此三角形必为
( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.以上三种情况都有可能[答案] B
[解析] ∵sinαcosβ<0,∴cosβ<0,
∴β是钝角,故选B.2.若角α的终边过点(-3,-2),则( )
A.sinαtanα>0 B.cosαtanα>0
C.sinαcosα>0 D.sinαcosα<0
[答案] C
[解析] ∵角α的终边过点(-3,-2),
∴sinα<0,cosα<0,tanα>0,
∴sinαcosα>0,故选C.3.角α满足条件sinα·cosα>0,sinα+cosα<0,则α在
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
[答案] C
[解析] ∵sinαcosα>0,sinα+cosα<0
∴sinα<0,cosα<0,∴α是第三象限角.[答案] B[答案] B[答案] D7.(2010·深圳中学)若sin2α>0且cosα<0,则α是
( )
A.第二象限角
B.第一或第三象限角
C.第三象限角
D.第二或第三象限角
[答案] C[点评] 要熟记三角函数值的符号与角终边位置的关系.[答案] B
[解析] 当θ在第一象限时,sinθ>0,cosθ>0,tanθ>0,排除A、D;当θ在第四象限时,sinθ<0,cosθ>0,tanθ<0,排除C,故选B.
