单位圆中的三角函数线

课件44张PPT。一、阅读教材P15～17回答
1．有向线段
带有 的线段叫做有向线段．方向2．单位圆中的三角函数线
设单位圆与x轴的正半轴交于点A，与角α的终边交于点P(x，y)，|OP|＝1.
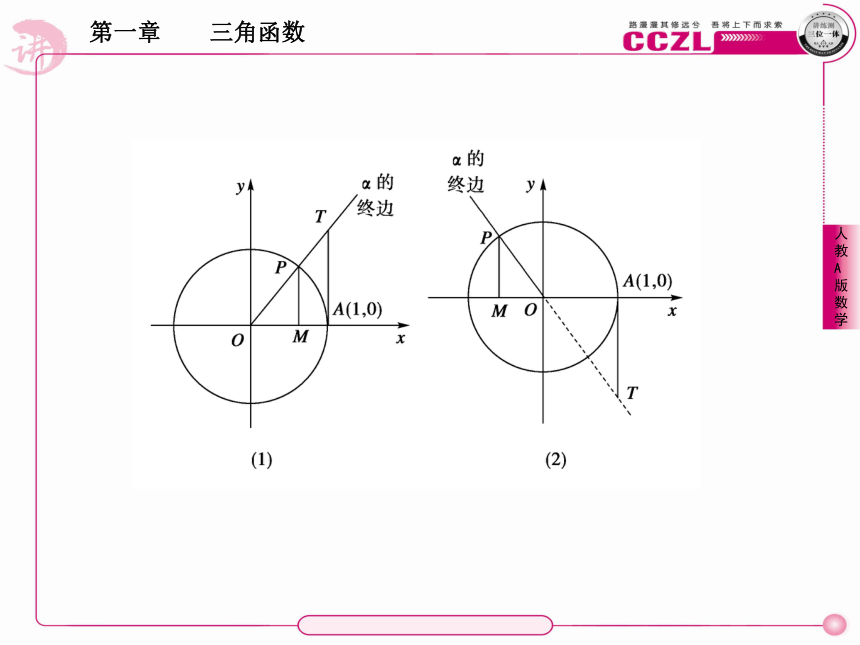
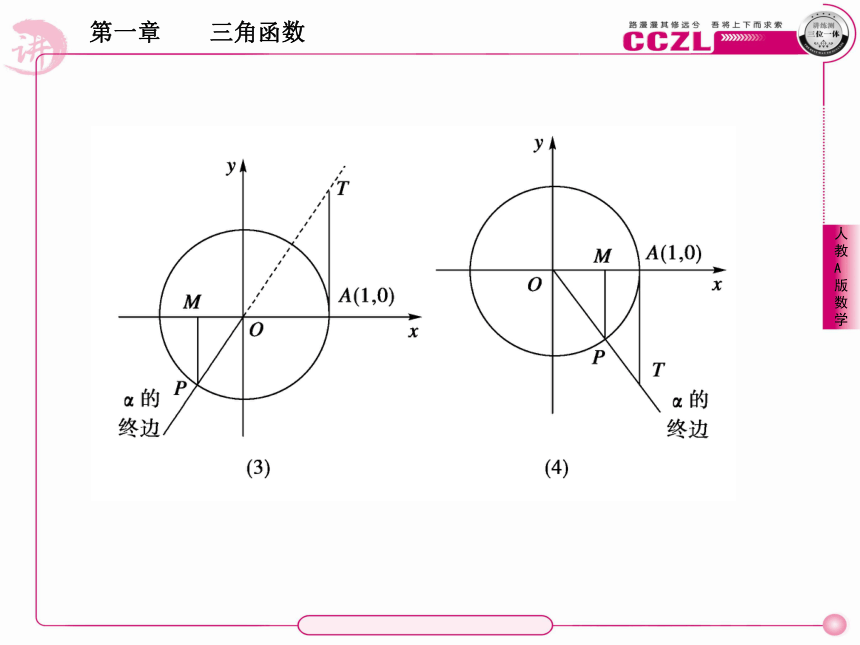
(1)当角α的终边不在坐标轴上时，过P作PM⊥x轴，M为垂足，过A作AT⊥x轴，与角α的终边(或其反向延长线)交于点T.
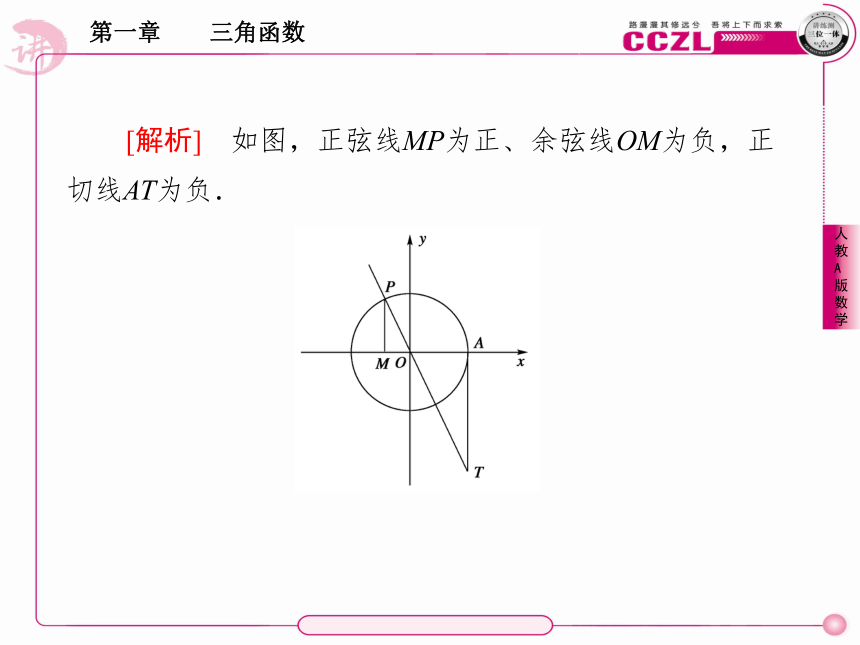
根据三角函数的定义可得：sinα＝ ，cosα＝ .yx如果我们规定有向线段MP与y轴的方向一致时取正值，相反时取负值，则可以用MP来表示sinα，即sinα＝MP，同样，规定OM与x轴方向相同时取正，相反时取负，则cosα＝OM，规定AT与y轴方向相同时取正，相反时取负，则tanα＝AT，把有向线段MP、OM、AT分别叫做角α的 线、 线、 线，如图．正弦余弦正切当角α的终边与x轴重合时，正弦线、正切线分别变成 ，此时角α的正弦值和正切值都为 ，余弦值为 ；当角α的终边与y轴重合时，余弦线变成 ，正切线不存在，此时角α的正切值 ，余弦值为 ，正弦值为 .一个点01或－1一个点不存在01或－1[解析]　如图，正弦线MP为正、余弦线OM为负，正切线AT为负．重点：用三角函数线表示任意角的三角函数值．
难点：应用三角函数线解决问题．应特别注意正弦线、余弦线、正切线的位置、方向、符号．
正弦线为α的终边与单位圆“交点”到x轴的垂直线段，由“垂足”指向“交点”，与y轴同向为正、反向为负；余弦线在x轴上，由“原点”指向“垂足”，与x轴同向为正，反向为负；正切线在过单位圆与x轴正向的交点的切线上，由“切点”指向与α终边的交点，与y轴同向为正，反向为负．
[分析]　先在单位圆中画出角θ的终边对应的区域，然后由各象限三角函数值的符号及大小变化规律确定函数值的变化范围，函数值为正时，有向线段越长值越大，函数值为负时，有向线段越长值越小．[解析]　如图所示，设角α的终边与单位圆相交于P(x，y)，过P作PQ⊥x轴，PR⊥y轴，Q、R为垂足．
(1)∵y＝sinα，x＝cosα，而在△OPQ中，QP＋OQ>OP.
∴sinα＋cosα>1.(2)∵0∴cos3αcos3α＋sin3α即cos3α＋sin3α<1.
[分析]　构造单位圆，利用单位圆中的三角函数线及三角形和扇形的面积来证明．一、选择题
1．下列判断中错误的是 (　　)
A．α一定时，单位圆中的正弦线一定
B．单位圆中有相同正弦线的角相等
C．α和α＋π有相同的正切线
D．有相同正切线的两个角的终边在同一直线上
[答案]　B
[解析]　有相同正弦线的角相差2π的整数倍，不一定相等，故选B.[答案]　D
[解析]　作出单位圆中的正弦线、余弦线，比较知D正确．4．若0≤θ<2π，则使tanθ≤1成立的角θ的取值范围是________________．5．(1)已知tanx>0，且sinx＋cosx>0，则角x的集合为____________．
(2)已知tanx<0，且sinx－cosx<0，则角x的集合为____________．
[答案]　(1){x|2kπ(2){x|2kπ－