1.3 三角函数的诱导公式
图片预览










文档简介
课件55张PPT。1.3 三角函数的诱导公式1.诱导公式二~四
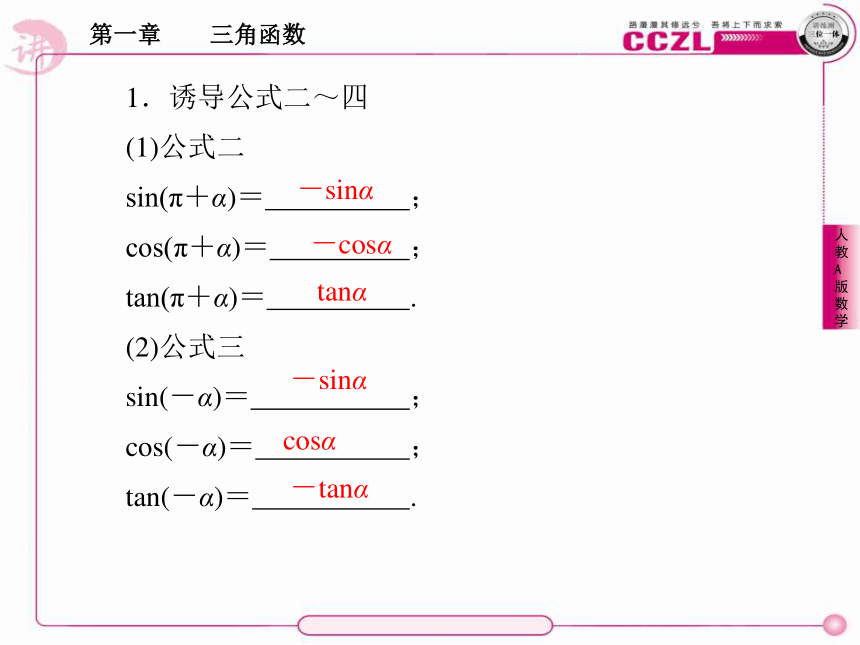
(1)公式二
sin(π+α)= ;
cos(π+α)= ;
tan(π+α)= .
(2)公式三
sin(-α)= ;
cos(-α)= ;
tan(-α)= .-sinα-cosαtanα-sinαcosα-tanα(3)公式四
sin(π-α)= ;
cos(π-α)= ;
tan(π-α)= .sinα-cosα-tanα2.公式一~四可以概括为
2kπ+α(k∈Z),-α,π±α的三角函数值,等于α的 函数值,前面加上一个 .同名把α看成锐角时原函数值的符号重点:诱导公式的探究,运用诱导公式进行简单三角函数式的求值、化简与恒等式的证明.
难点:从单位圆的对称性与任意角终边的对称性中发现问题,提出研究方法.
1.诱导公式的记忆方法
诱导公式一~四可用口诀“函数名不变,符号看象限”记忆,其中“函数名不变”是指等式两边的三角函数同名,“符号”是指等号右边是正号还是负号,“看象限”是指把α看成锐角时原三角函数中角所在的象限.2.公式的推导过程应借助单位圆重点领会π±α,-α与角α的终边的对称关系,从而找出其终边与单位圆的交点的坐标关系.进而利用任意角的三角函数的定义导出公式.3.应用诱导公式把任意角的三角函数化为锐角的三角函数的步骤.一般遵循:负化正→正化主→主化锐→求值(习惯上称[0,2π)为主区间),即
还要注意灵活运用.
4.通过诱导公式的学习,要深刻领会化归与转化的思想.
(3)tan(-855°)=-tan855°
=-tan(2×360°+135°)=-tan135°
=-tan(180°-45°)=tan45°=1.
[点评] 要养成解题前分析,解题后反思的习惯,以提高灵活应用诱导公式的能力.[答案] (1)0 (2)0(2)原式
=tan10°+tan(180°-10°)+sin(5×360°+66°)-sin[(-2)×360°+114°]
=tan10°-tan10°+sin66°-sin114°
=sin66°-sin(180°-66°)
=sin66°-sin66°=0.[分析] 先观察角的特点,选用恰当的诱导公式化简,然后依据同角关系式求解.[答案] -1
[分析] 由于k的奇偶性影响到sin(kπ-α),cos(kπ+α)等的结果,故应对k分奇偶讨论.[分析] 由已知出发可求出tanα的值,利用诱导公式可把被求式转化为含sinα与cosα的齐次式,这样进行适当的变形后可将其表示为关于tanα的表示式,代入值即可求解.[点评] 已知某式的三角函数值,求其它式子的三角函数值,关键是寻求已知式与被求式的内在联系,恰当选择公式,体现了把未知问题转化为已知问题的数学思想.
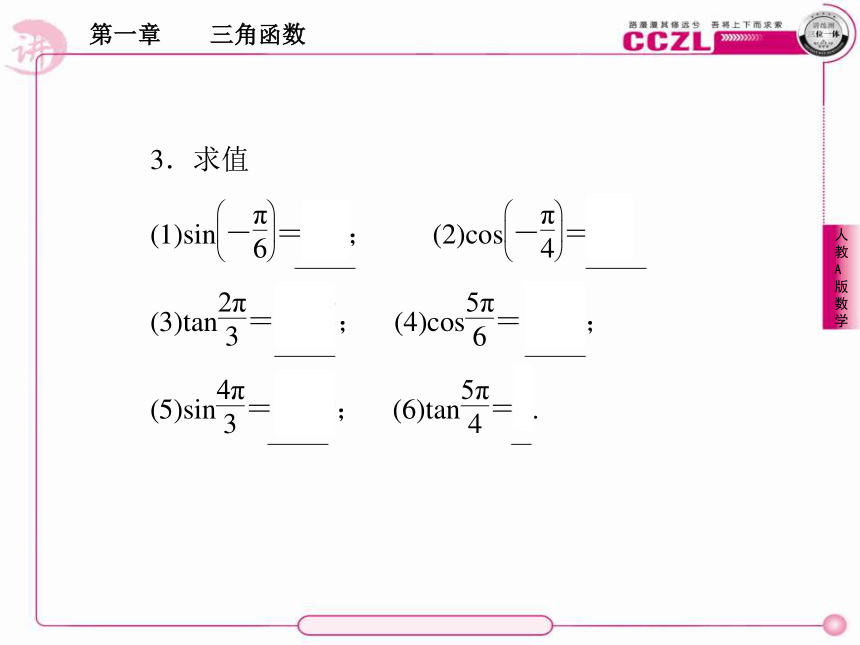
若cos165°=a,则tan195°=________.[分析] 题中所给条件式比较繁琐,故先化简,然后利用平方关系消去α(或β)解方程可求出角α与β的一个三角函数值和其范围,进一步求出角.[辨析] 应用平方关系sin2α+cos2α=1,由sinα=a,求cosα的值时,应依据角α的范围判定cosα的符号.[答案] D[答案] C[答案] A4.cos1030°等于
( )
A.cos50° B.-cos50°
C.sin50° D.-sin50°
[答案] A
[解析] cos1030°=cos(3×360°-50°)=cos(-50°)=cos50°.[答案] B
[解析] 在使用诱导公式求三角函数值时,一般可按以下步骤进行:先化负角为正角,再去掉圆周角k·360°,k∈Z,最后化0°~360°间的角为锐角.7.已知tan(π+α)=3,则sin(π+α)·cos(π-α)=________.8.cos1°+cos2°+cos3°+…+cos180°=________.
[答案] -1
[解析] 原式=(cos1°+cos179°)+(cos2°+cos178°)+…+(cos89°+cos91°)+cos90°+cos180°
=0+0+…+0+0+0+(-1)=-1.
(1)公式二
sin(π+α)= ;
cos(π+α)= ;
tan(π+α)= .
(2)公式三
sin(-α)= ;
cos(-α)= ;
tan(-α)= .-sinα-cosαtanα-sinαcosα-tanα(3)公式四
sin(π-α)= ;
cos(π-α)= ;
tan(π-α)= .sinα-cosα-tanα2.公式一~四可以概括为
2kπ+α(k∈Z),-α,π±α的三角函数值,等于α的 函数值,前面加上一个 .同名把α看成锐角时原函数值的符号重点:诱导公式的探究,运用诱导公式进行简单三角函数式的求值、化简与恒等式的证明.
难点:从单位圆的对称性与任意角终边的对称性中发现问题,提出研究方法.
1.诱导公式的记忆方法
诱导公式一~四可用口诀“函数名不变,符号看象限”记忆,其中“函数名不变”是指等式两边的三角函数同名,“符号”是指等号右边是正号还是负号,“看象限”是指把α看成锐角时原三角函数中角所在的象限.2.公式的推导过程应借助单位圆重点领会π±α,-α与角α的终边的对称关系,从而找出其终边与单位圆的交点的坐标关系.进而利用任意角的三角函数的定义导出公式.3.应用诱导公式把任意角的三角函数化为锐角的三角函数的步骤.一般遵循:负化正→正化主→主化锐→求值(习惯上称[0,2π)为主区间),即
还要注意灵活运用.
4.通过诱导公式的学习,要深刻领会化归与转化的思想.
(3)tan(-855°)=-tan855°
=-tan(2×360°+135°)=-tan135°
=-tan(180°-45°)=tan45°=1.
[点评] 要养成解题前分析,解题后反思的习惯,以提高灵活应用诱导公式的能力.[答案] (1)0 (2)0(2)原式
=tan10°+tan(180°-10°)+sin(5×360°+66°)-sin[(-2)×360°+114°]
=tan10°-tan10°+sin66°-sin114°
=sin66°-sin(180°-66°)
=sin66°-sin66°=0.[分析] 先观察角的特点,选用恰当的诱导公式化简,然后依据同角关系式求解.[答案] -1
[分析] 由于k的奇偶性影响到sin(kπ-α),cos(kπ+α)等的结果,故应对k分奇偶讨论.[分析] 由已知出发可求出tanα的值,利用诱导公式可把被求式转化为含sinα与cosα的齐次式,这样进行适当的变形后可将其表示为关于tanα的表示式,代入值即可求解.[点评] 已知某式的三角函数值,求其它式子的三角函数值,关键是寻求已知式与被求式的内在联系,恰当选择公式,体现了把未知问题转化为已知问题的数学思想.
若cos165°=a,则tan195°=________.[分析] 题中所给条件式比较繁琐,故先化简,然后利用平方关系消去α(或β)解方程可求出角α与β的一个三角函数值和其范围,进一步求出角.[辨析] 应用平方关系sin2α+cos2α=1,由sinα=a,求cosα的值时,应依据角α的范围判定cosα的符号.[答案] D[答案] C[答案] A4.cos1030°等于
( )
A.cos50° B.-cos50°
C.sin50° D.-sin50°
[答案] A
[解析] cos1030°=cos(3×360°-50°)=cos(-50°)=cos50°.[答案] B
[解析] 在使用诱导公式求三角函数值时,一般可按以下步骤进行:先化负角为正角,再去掉圆周角k·360°,k∈Z,最后化0°~360°间的角为锐角.7.已知tan(π+α)=3,则sin(π+α)·cos(π-α)=________.8.cos1°+cos2°+cos3°+…+cos180°=________.
[答案] -1
[解析] 原式=(cos1°+cos179°)+(cos2°+cos178°)+…+(cos89°+cos91°)+cos90°+cos180°
=0+0+…+0+0+0+(-1)=-1.
