1．4 三角函数的图象与性质

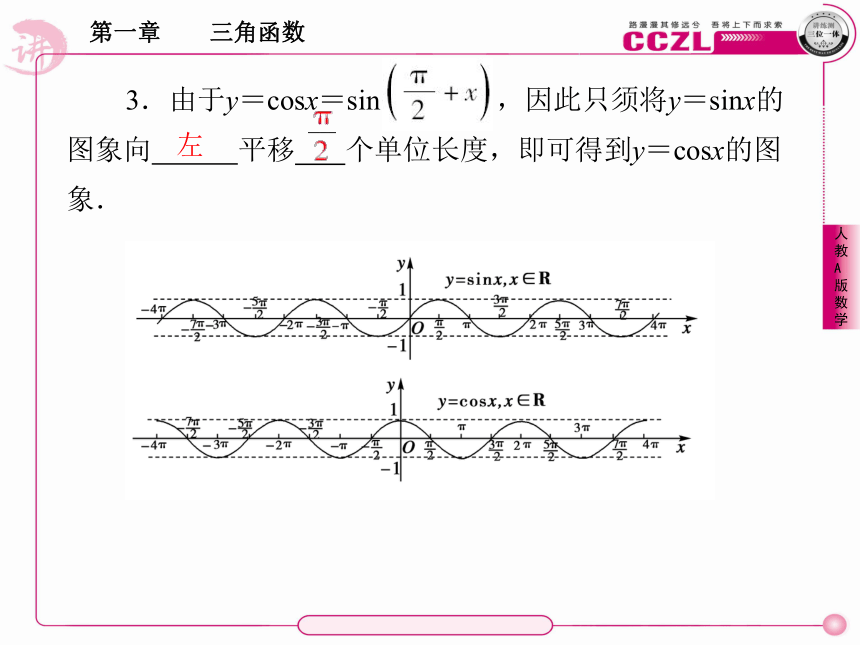
课件35张PPT。1．4　三角函数的图象与性质x x 正弦 终点 因为终边相同的角有相同的三角函数值，所以函数y＝sinx，x∈[2kπ，2(k＋1)π)，k∈Z且k≠0的图象，与函数y＝sinx，x∈[0,2π)的图象的形状完全一致．于是只要将函数y＝sinx，x∈[0,2π)的图象向左、向右平行移动(每次移动 个单位长度)，就可以得到正弦函数y＝sinx，x∈R的图象．2π2．观察函数y＝sinx，x∈[0,2π]的图象上，起关键作用的点有以下五个：在精确度要求不太高时，我们常常先找出这五个关键点，再用 的曲线将它们连接起来，就得到函数的简图．这种近似作图的方法，习惯上称作“ ”．光滑五点法3．由于y＝cosx＝sin ，因此只须将y＝sinx的图象向 平移 个单位长度，即可得到y＝cosx的图象．左由此可知，在余弦函数y＝cosx(0≤x≤2π)的图象上起关键作用的五个点是 ， ， ， ， ．(0,1)(2π，1)( π，1)重点：正弦函数、余弦函数的图象．
难点：将单位圆的正弦线通过平移转化为正弦函数图象上的点；正弦函数和余弦函数图象间的关系．2．画三角函数的图象一般采用“五点法”，三角函数图象上的五个关键点，大致反映了三角函数的图象特征和三角函数的性质，应熟练掌握．
3．要熟悉正弦曲线、余弦曲线的形状、位置、分布特征，要熟练掌握其五个关键点，弄清正弦曲线与余弦曲线的关系．
[例1]　作出下列函数的图象：
(1)y＝－sinx(0≤x≤2π)；
(2)y＝1＋cosx(0≤x≤2π)．
[分析]　找出起关键作用的五个点，描点作图．[解析]　(1)列表：描点连线，如图．(2)列表：描点连线，如图．
用五点法作函数y＝2－sinx，x∈[0,2π]的图象．
[解析]　(1)列表：(2)描点、连线：(图形如下)
[例2]　利用图象变换作出下列函数的简图：
(1)y＝1－cosx，x∈[0,2π]．
(2)y＝|sinx|，x∈[0,4π]．
[解析]　(1)首先用五点法作出函数y＝cosx，x∈[0,2π]的图象，再作出y＝cosx关于x轴对称的图象，最后将图象向上平移1个单位．如图(1)所示．(2)首先用五点法作出函数y＝sinx，x∈[0,4π]的图象，再将x轴下方的部分对称到x轴的上方．如图(2)所示．[点评]　函数的图象变换除了平移变换外，还有对称变换．如本例．一般地，函数f(x)的图象与f(－x)的图象关于y轴对称；－f(x)的图象与f(x)的图象关于x轴对称；－f(－x)的图象与f(x)的图象关于原点对称；f(|x|)的图象关于y轴对称．
利用图象变换作出函数y＝sin|x|，x∈[－2π，2π]的简图．一、填空题
1．观察正弦函数的图象可见，y＝sinx的最大值为________，最小值为________，图象关于直线________轴对称，关于点________中心对称．2．观察余弦函数的图象可见y＝cosx的最大值为________，最小值为________，图象关于直线________成轴对称，关于点________成中心对称．3．将y＝cosx的图象向________平移________个单位可以得到y＝sinx的图象．二、解答题
4．在[0,2π]内，作出y＝2sinx的图象．
[解析]　按五个关键点列表：描点并用光滑的曲线连结起来．