正弦函数、余弦函数的图像和性质
文档属性
| 名称 | 正弦函数、余弦函数的图像和性质 |  | |
| 格式 | rar | ||
| 文件大小 | 516.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-29 22:02:00 | ||
图片预览











文档简介
课件61张PPT。一、1.周期函数的定义
一般地,对于函数y=f(x),如果存在一个 的常数T,使得当x取定义域内的每一个值时, 都成立,那么就把函数y=f(x)叫做 ,不为零的常数T叫做这个函数的 .
2.y=sinx,y=cosx都是周期函数,其周期是 ,最小正周期是 .不为零f(x+T)=f(x)周期函数周期2kπ(k∈Z,k≠0)2π3.y=Asin(ωx+φ)(A≠0,ω≠0)的最小正周期为
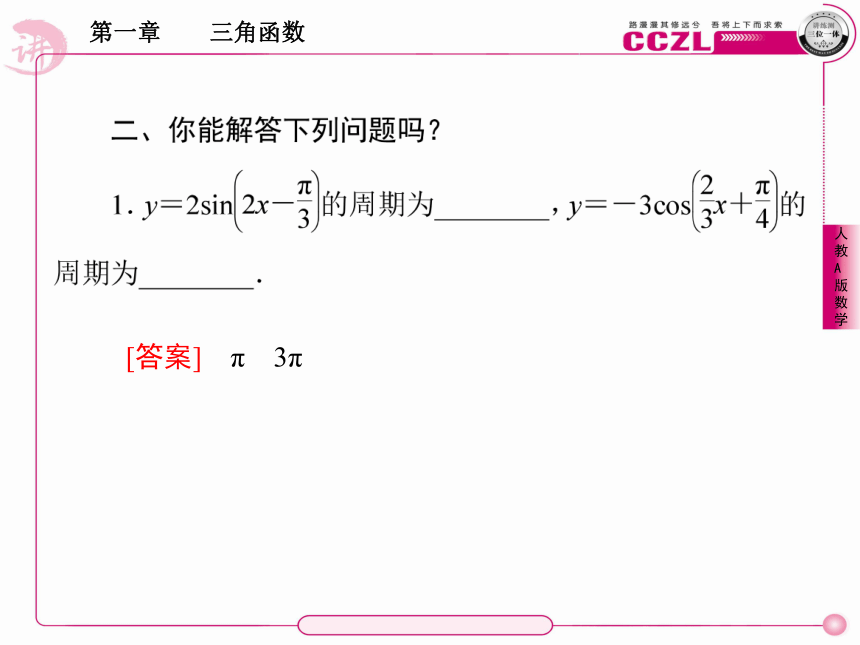
.5.y=cosx(x∈R)的奇偶性为: 函数;单调性为:在每一个区间 上都是增函数,在每一个区间 上都是减函数;图象的对称特征为:关于每一个点 成中心对称,关于每一条直线 成轴对称;当x= 时,y取最大值 ,当x= 时,y取最小值 .偶[2kπ-π,2kπ](k∈Z)[2kπ,2kπ+π](k∈Z)x=kπ(k∈Z)2kπ(k∈Z)12kπ+π(k∈Z)-1[答案] π 3π2.函数y=3sinx的最大值为________,取到最大值时,x的取值集合为________.3.函数y=-2cosx的最小值为________,取到最小值时,x的取值集合为________.
[答案] -2 {x|x=2kπ,k∈Z}[答案] A重点:正弦函数、余弦函数的性质.
难点:①函数周期的理解.
②函数在每一个单调区间上的单调性与在定义域上不单调的特征.
③函数图象的对称性.1.对函数周期的理解需注意以下几点:
(1)一定要注意是对定义域内的每一个值都有f(x+T)=f(x)成立,即x的任意性,否则不能说y=f(x)是周期函数,自然也就没有周期T.
(2)周期T并不唯一,即若T为函数y=f(x)的周期,则2T,3T,…,nT,n∈Z,都为其周期.
(3)由于周期的不唯一性,为了研究的方便,我们需要确定一个可以方便研究的T,于是,若所有的周期中,存在一个最小的正数,我们便称它为最小正周期,以后若没有特别指出,往往指的是最小正周期.(4)并非所有周期函数都有最小正周期.例如,对于常数函数f(x)=c(c为常数,x∈R),所有非零实数T都是它的周期,而最小正数不存在,所以常数函数没有最小正周期.
(5)周期函数的定义域:如果f(x)是周期函数,T为其周期,那么x+kT(k∈Z)也属于其定义域,也就是说,周期函数的定义域是一个无限集.3.正弦函数、余弦函数都有无穷多个单调区间,但在两个单调增(或减)区间的并集上不单调,这一点要特别注意.
4.正弦(余弦)函数的对称轴一定经过图象的最高(或最低)点,对称中心在x轴上.
[分析] 根据函数奇偶性定义进行判断,先检查定义域是否关于原点为对称区间,如果是,再验证f(-x)是否等于-f(x)或f(x),进而判断函数的奇偶性;如果不是,则该函数必为非奇非偶函数.A.奇函数 B.偶函数
C.非奇非偶函数 D.以上都不对
[答案] B[分析] 三角函数值的大小比较,一般考虑应用诱导公式化到同一个单调区间内;有时候也用三角函数线等方法比较其大小,不同名的欲应用单调性,须先化同名.[点评] 比较两个函数值大小时,一般先利用诱导公式把它们化为同名三角函数,再把它们转化到同一单调区间上,利用函数单调性对它们进行比较.[辨析] 解答忽视了以下内容:三角形中的最小角θ的范围不是0°<θ<90°,而是0°<θ≤60°,又∵三角形是不等边三角形,故0°<θ<60°.[答案] D[答案] C[答案] B4.sin1°、sin1、sinπ°的大小顺序是( )
A.sin1°C.sinπ°[答案] B
[解析] 1弧度=57.3°,
∵y=sinx在(0°,90°)上是增函数,且1°<π°<1,
∴sin1°( )
①y=x2sinx; ②y=sinx,x∈[0,2π];
③y=sinx,x∈[-π,π]; ④y=xcosx.
A.1个 B.2个 C.3个 D.4个
[答案] C
[解析] ∵y=sinx,x∈[0,2π]的定义域不关于原点对称,∴②不是奇函数,
①、③、④符合奇函数的概念.6.y=2sinx2的值域是
( )
A.[-2,2] B.[0,2]
C.[-2,0] D.R
[答案] A
[解析] ∵x2≥0,∴sinx2∈[-1,1],
∴y=2sinx2∈[-2,2].8.函数y=asinx-b的最大值为1,最小值为-7,则a=________,b=________.
[答案] ±4 3
一般地,对于函数y=f(x),如果存在一个 的常数T,使得当x取定义域内的每一个值时, 都成立,那么就把函数y=f(x)叫做 ,不为零的常数T叫做这个函数的 .
2.y=sinx,y=cosx都是周期函数,其周期是 ,最小正周期是 .不为零f(x+T)=f(x)周期函数周期2kπ(k∈Z,k≠0)2π3.y=Asin(ωx+φ)(A≠0,ω≠0)的最小正周期为
.5.y=cosx(x∈R)的奇偶性为: 函数;单调性为:在每一个区间 上都是增函数,在每一个区间 上都是减函数;图象的对称特征为:关于每一个点 成中心对称,关于每一条直线 成轴对称;当x= 时,y取最大值 ,当x= 时,y取最小值 .偶[2kπ-π,2kπ](k∈Z)[2kπ,2kπ+π](k∈Z)x=kπ(k∈Z)2kπ(k∈Z)12kπ+π(k∈Z)-1[答案] π 3π2.函数y=3sinx的最大值为________,取到最大值时,x的取值集合为________.3.函数y=-2cosx的最小值为________,取到最小值时,x的取值集合为________.
[答案] -2 {x|x=2kπ,k∈Z}[答案] A重点:正弦函数、余弦函数的性质.
难点:①函数周期的理解.
②函数在每一个单调区间上的单调性与在定义域上不单调的特征.
③函数图象的对称性.1.对函数周期的理解需注意以下几点:
(1)一定要注意是对定义域内的每一个值都有f(x+T)=f(x)成立,即x的任意性,否则不能说y=f(x)是周期函数,自然也就没有周期T.
(2)周期T并不唯一,即若T为函数y=f(x)的周期,则2T,3T,…,nT,n∈Z,都为其周期.
(3)由于周期的不唯一性,为了研究的方便,我们需要确定一个可以方便研究的T,于是,若所有的周期中,存在一个最小的正数,我们便称它为最小正周期,以后若没有特别指出,往往指的是最小正周期.(4)并非所有周期函数都有最小正周期.例如,对于常数函数f(x)=c(c为常数,x∈R),所有非零实数T都是它的周期,而最小正数不存在,所以常数函数没有最小正周期.
(5)周期函数的定义域:如果f(x)是周期函数,T为其周期,那么x+kT(k∈Z)也属于其定义域,也就是说,周期函数的定义域是一个无限集.3.正弦函数、余弦函数都有无穷多个单调区间,但在两个单调增(或减)区间的并集上不单调,这一点要特别注意.
4.正弦(余弦)函数的对称轴一定经过图象的最高(或最低)点,对称中心在x轴上.
[分析] 根据函数奇偶性定义进行判断,先检查定义域是否关于原点为对称区间,如果是,再验证f(-x)是否等于-f(x)或f(x),进而判断函数的奇偶性;如果不是,则该函数必为非奇非偶函数.A.奇函数 B.偶函数
C.非奇非偶函数 D.以上都不对
[答案] B[分析] 三角函数值的大小比较,一般考虑应用诱导公式化到同一个单调区间内;有时候也用三角函数线等方法比较其大小,不同名的欲应用单调性,须先化同名.[点评] 比较两个函数值大小时,一般先利用诱导公式把它们化为同名三角函数,再把它们转化到同一单调区间上,利用函数单调性对它们进行比较.[辨析] 解答忽视了以下内容:三角形中的最小角θ的范围不是0°<θ<90°,而是0°<θ≤60°,又∵三角形是不等边三角形,故0°<θ<60°.[答案] D[答案] C[答案] B4.sin1°、sin1、sinπ°的大小顺序是( )
A.sin1°
[解析] 1弧度=57.3°,
∵y=sinx在(0°,90°)上是增函数,且1°<π°<1,
∴sin1°
①y=x2sinx; ②y=sinx,x∈[0,2π];
③y=sinx,x∈[-π,π]; ④y=xcosx.
A.1个 B.2个 C.3个 D.4个
[答案] C
[解析] ∵y=sinx,x∈[0,2π]的定义域不关于原点对称,∴②不是奇函数,
①、③、④符合奇函数的概念.6.y=2sinx2的值域是
( )
A.[-2,2] B.[0,2]
C.[-2,0] D.R
[答案] A
[解析] ∵x2≥0,∴sinx2∈[-1,1],
∴y=2sinx2∈[-2,2].8.函数y=asinx-b的最大值为1,最小值为-7,则a=________,b=________.
[答案] ±4 3
