高中数学必修3课件:2.2用样本的数据特征估计总体的数据特征(新人教A版)
文档属性
| 名称 | 高中数学必修3课件:2.2用样本的数据特征估计总体的数据特征(新人教A版) |  | |
| 格式 | rar | ||
| 文件大小 | 41.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-30 21:39:00 | ||
图片预览








文档简介
课件20张PPT。2.2.2 用样本的数字特征
估计总体的数字特征第二课时 统 计
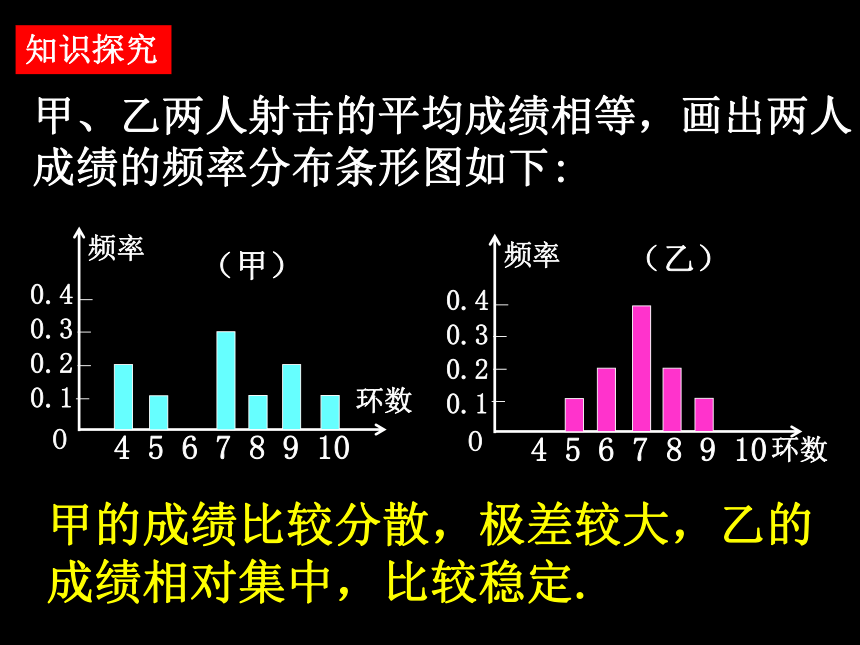
高中数学必修3第二章知识回顾 如何根据样本频率分布直方图,分别估计总体的众数、中位数和平均数?(1)众数:最高矩形下端中点的横坐标.(2)中位数:直方图面积平分线与横轴交点的横坐标.(3)平均数:每个小矩形的面积与小矩形底边中点的横坐标的乘积之和. 在一次射击选拔赛中,甲、乙两名运动员各射击10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
甲、乙两人本次射击的平均成绩分别为多少环?哪一个运动员成绩比较稳定?知识探究甲、乙两人射击的平均成绩相等,画出两人成绩的频率分布条形图如下:甲的成绩比较分散,极差较大,乙的成绩相对集中,比较稳定.知识探究 对于样本数据x1,x2,…,xn,
设想通过各数据到其平均数的平均距离来反映样本数据的分散程度,那么这个平均距离如何计算? 知识探究最常用的统计量是标准差,一般用s表示.知识探究假设样本数据x1,x2,…,xn的平均数为 ,
则标准差的计算公式是:s甲=2,s乙=1.095. 知识探究(1)标准差越大离散程度越大,数据较分
散;标准差越小离散程度越小,数据
较集中在平均数周围. 注意:(2)标准差为0的样本数据都相等. 知识补充方差:标准差的平方就是方差其中样本数据x1,x2,…,xn的平均数为知识补充 方差与标准差都是用来描述一组数据
波动情况的特征数.在实际应用中一般多
采用标准差.例题分析 画出下列四组样本数据的条形图,
说明他们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;例1(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
甲、乙两人同时生产内径为25.40mm的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各随机抽取20件,量得其内径尺寸如下(单位:mm):甲 :
25.46 25.32 25.45 25.39 25.36 25.34 25.42 25.45 25.38 25.42 25.39 25.43 25.39 25.40 25.44 25.40 25.42 25.35 25.41 25.39乙:
25.40 25.43 25.44 25.48 25.48 25.47 25.49 25.49 26.36 25.34 25.33 25.43 25.43 25.32 25.47 25.31 25.32 25.32 25.32 25.48 从生产零件内径的尺寸看,谁生产的零件质量较高? 例2 甲生产的零件内径更接近内径标准,且稳定程度较高,故甲生产的零件质量较高.
生产质量可以从总体的平均数与标准差两个角度来衡量. 用样本的平均数与标准差估计总体的平均数与标准差.典例分析 以往招生统计显示,某所大学录取的新生高考总分的中位数基本稳定在550分,若某同学今年高考得了520分,他想报考这所大学还需收集哪些信息?要点:(1)查往年录取的新生的平均分数.若平均数小于中位数很多,说明最低录取线较低,可以报考;
(2)查往年录取的新生高考总分的标准差.若标准差较大,说明新生的录取分数较分散,最低录取线可能较低,可以考虑报考.例3 有20种不同的零食,它们的热量含量如下:
110 120 123 165 432 190 174 235 428 318 249 280 162 146 210 120 123 120 150 140(1)以上20个数据组成总体,求总体平均数与总体标准差;
(2)设计一个适当的随机抽样方法,从总体中抽取一个容量为7的样本,计算样本的平均数和标准差.例4(1)总体平均数为199.75,总体标准差为95.26.(1)以上20个数据组成总体,求总体平均数与总体标准差;
(2)设计一个适当的随机抽样方法,从总体中抽取一个容量为7的样本,计算样本的平均数和标准差.(2)可以用抽签法抽取样本,样本的平均数和标准差与抽取的样本有关.小结作业1.对同一个总体,可以抽取不同的样本,相应的平均数与标准差都会发生改变.如果样本的代表性差,则对总体所作的估计就会产生偏差;如果样本没有代表性,则对总体作出错误估计的可能性就非常大,由此可见抽样方法的重要性.2.在抽样过程中,抽取的样本是具有随机性的,如从一个包含6个个体的总体中抽取一个容量为3的样本就有20中可能抽样,因此样本的数字特征也有随机性.
用样本的数字特征估计总体的数字特征,是一种统计思想,没有惟一答案.3.在实际应用中,调查统计是一个探究性学习过程,需要做一系列工作,我们可以把学到的知识应用到自主研究性课题中去.作业:
《学海》第7、8课时
估计总体的数字特征第二课时 统 计
高中数学必修3第二章知识回顾 如何根据样本频率分布直方图,分别估计总体的众数、中位数和平均数?(1)众数:最高矩形下端中点的横坐标.(2)中位数:直方图面积平分线与横轴交点的横坐标.(3)平均数:每个小矩形的面积与小矩形底边中点的横坐标的乘积之和. 在一次射击选拔赛中,甲、乙两名运动员各射击10次,每次命中的环数如下:
甲:7 8 7 9 5 4 9 10 7 4
乙:9 5 7 8 7 6 8 6 7 7
甲、乙两人本次射击的平均成绩分别为多少环?哪一个运动员成绩比较稳定?知识探究甲、乙两人射击的平均成绩相等,画出两人成绩的频率分布条形图如下:甲的成绩比较分散,极差较大,乙的成绩相对集中,比较稳定.知识探究 对于样本数据x1,x2,…,xn,
设想通过各数据到其平均数的平均距离来反映样本数据的分散程度,那么这个平均距离如何计算? 知识探究最常用的统计量是标准差,一般用s表示.知识探究假设样本数据x1,x2,…,xn的平均数为 ,
则标准差的计算公式是:s甲=2,s乙=1.095. 知识探究(1)标准差越大离散程度越大,数据较分
散;标准差越小离散程度越小,数据
较集中在平均数周围. 注意:(2)标准差为0的样本数据都相等. 知识补充方差:标准差的平方就是方差其中样本数据x1,x2,…,xn的平均数为知识补充 方差与标准差都是用来描述一组数据
波动情况的特征数.在实际应用中一般多
采用标准差.例题分析 画出下列四组样本数据的条形图,
说明他们的异同点.
(1) 5,5,5,5,5,5,5,5,5;
(2) 4,4,4,5,5,5,6,6,6;例1(3) 3,3,4,4,5,6,6,7,7;
(4) 2,2,2,2,5,8,8,8,8.
甲、乙两人同时生产内径为25.40mm的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各随机抽取20件,量得其内径尺寸如下(单位:mm):甲 :
25.46 25.32 25.45 25.39 25.36 25.34 25.42 25.45 25.38 25.42 25.39 25.43 25.39 25.40 25.44 25.40 25.42 25.35 25.41 25.39乙:
25.40 25.43 25.44 25.48 25.48 25.47 25.49 25.49 26.36 25.34 25.33 25.43 25.43 25.32 25.47 25.31 25.32 25.32 25.32 25.48 从生产零件内径的尺寸看,谁生产的零件质量较高? 例2 甲生产的零件内径更接近内径标准,且稳定程度较高,故甲生产的零件质量较高.
生产质量可以从总体的平均数与标准差两个角度来衡量. 用样本的平均数与标准差估计总体的平均数与标准差.典例分析 以往招生统计显示,某所大学录取的新生高考总分的中位数基本稳定在550分,若某同学今年高考得了520分,他想报考这所大学还需收集哪些信息?要点:(1)查往年录取的新生的平均分数.若平均数小于中位数很多,说明最低录取线较低,可以报考;
(2)查往年录取的新生高考总分的标准差.若标准差较大,说明新生的录取分数较分散,最低录取线可能较低,可以考虑报考.例3 有20种不同的零食,它们的热量含量如下:
110 120 123 165 432 190 174 235 428 318 249 280 162 146 210 120 123 120 150 140(1)以上20个数据组成总体,求总体平均数与总体标准差;
(2)设计一个适当的随机抽样方法,从总体中抽取一个容量为7的样本,计算样本的平均数和标准差.例4(1)总体平均数为199.75,总体标准差为95.26.(1)以上20个数据组成总体,求总体平均数与总体标准差;
(2)设计一个适当的随机抽样方法,从总体中抽取一个容量为7的样本,计算样本的平均数和标准差.(2)可以用抽签法抽取样本,样本的平均数和标准差与抽取的样本有关.小结作业1.对同一个总体,可以抽取不同的样本,相应的平均数与标准差都会发生改变.如果样本的代表性差,则对总体所作的估计就会产生偏差;如果样本没有代表性,则对总体作出错误估计的可能性就非常大,由此可见抽样方法的重要性.2.在抽样过程中,抽取的样本是具有随机性的,如从一个包含6个个体的总体中抽取一个容量为3的样本就有20中可能抽样,因此样本的数字特征也有随机性.
用样本的数字特征估计总体的数字特征,是一种统计思想,没有惟一答案.3.在实际应用中,调查统计是一个探究性学习过程,需要做一系列工作,我们可以把学到的知识应用到自主研究性课题中去.作业:
《学海》第7、8课时
