高中数学必修3课件:3.1.3 概率的基本性质(新人教A版)
文档属性
| 名称 | 高中数学必修3课件:3.1.3 概率的基本性质(新人教A版) |

|
|
| 格式 | rar | ||
| 文件大小 | 66.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-30 00:00:00 | ||
图片预览






文档简介
课件24张PPT。3.1.3 概率的基本性质
高中数学必修3第三章《概率》创设情境 我们可以把一次试验可能出现的结果看成一个集合(如连续抛掷两枚硬币),那么必然事件对应全集,随机事件对应子集,不可能事件对应空集,类比集合的关系与运算,事件之间存在怎样的关系与运算呢?1. 事件的关系与运算 在掷骰子试验中,我们用集合形式定义如下
事件:C1={出现1点},C2={出现2点},
C3={出现3点},C4={出现4点},
C5={出现5点},C6={出现6点},
D1={出现的点数不大于1},
D2={出现的点数大于4},
D3={出现的点数小于6},
E={出现的点数小于7},
F={出现的点数大于6},
G={出现的点数为偶数},
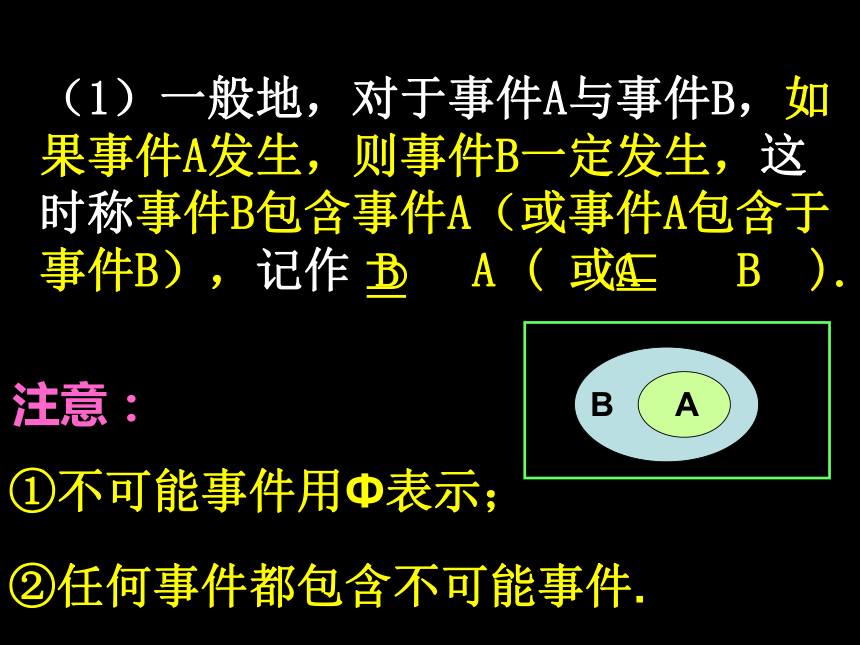
H={出现的点数为奇数}。如果事件C1发生,则一定有哪些事件发生?集合C1与这些集合之间的关系怎样描述? (1)一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或事件A包含于事件B),记作 B A ( 或A B ).②任何事件都包含不可能事件.①不可能事件用Ф表示;注意:分析事件C1={出现1点}
与事件D1={出现的点数不大于1},之间的包含关系,按集合观点这两
个事件之间的关系应怎样描述? (2)一般地,如果事件A发生,则事件B一定发生,反之也成立,这时称这两个事件相等,
记作:A=B . 若B A,且A B,则称事件A与事件B相等,记作A=B. 在掷骰子试验中,我们用集合形式定义如下事件:C1={出现1点},C2={出现2点}
C3={出现3点},C4={出现4点},
C5={出现5点},C6={出现6点},
D1={出现的点数不大于1},
D2={出现的点数大于4},
D3={出现的点数小于6},
E={出现的点数小于7},
F={出现的点数大于6},
G={出现的点数为偶数},
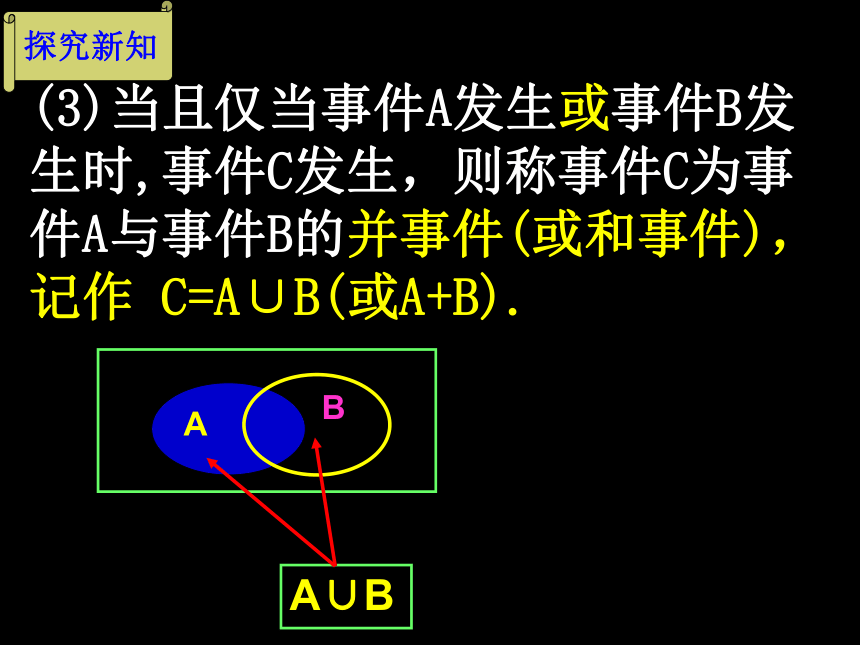
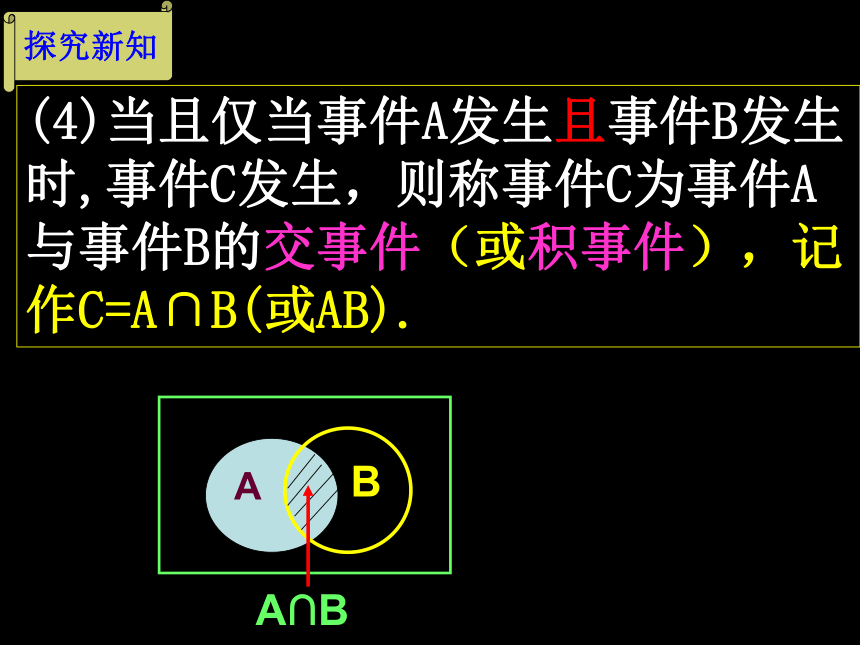
H={出现的点数为奇数},等等.如果事件C5发生或C6发生,就意味着哪个事件发生?反之成立吗? (3)当且仅当事件A发生或事件B发生时,事件C发生,则称事件C为事件A与事件B的并事件(或和事件),记作 C=A∪B(或A+B). 探究新知A∪BAB探究新知(4)当且仅当事件A发生且事件B发生时,事件C发生,则称事件C为事件A与事件B的交事件(或积事件),记作C=A∩B(或AB).A∩BAB探究新知(5)若A∩B为不可能事件(A∩B=Ф)此时,称事件A与事件B互斥.在一次试验中,事件A与事件B不能同时发生.含义:探究新知(6)若A∩B为不可能事件,A∪B为必然事件,则称事件A与事件B互为对立事件.若事件A与事件B不能同时发生,且事件A与事件B必有一个发生.含义:运用新知1.事件A与事件B的和事件、积事件,分别对应两个集合的并、交,那么事件A与事件B互为对立事件,对应的集合A、B是什么关系?集合A与集合B互为补集.2.给定下列命题,判断对错。(1)互斥事件一定对立;(2)对立事件一定互斥;3.一个射手进行一次射击,试判定下列
事件哪些是互斥事件?哪些是对立事件?(1)事件A:命中环数大于7;(2)事件B:命中环数为10环;(3)事件C:命中环数小于6;(4)事件D:命中环数为6、 7、8、9、10.事件C与事件D互斥且对立.事件A与事件C互斥,事件B与事件C互斥2.概率的几个基本性质(1)概率P(A)的取值范围②不可能事件C一定不发生, 则P(C)=0①必然事件B一定发生, 则 P(B)=1③随机事件A发生的概率为0<P(A)<1(2)概率的加法公式如果事件A与事件B互斥,则 P(A∪B)=P(A)+P(B).特别地,若事件A与事件B互为
对立事件,则P(A)+P(B)=1. 运用新知4.一个人打靶时连续射击两次事件“至少有一次中靶”的互斥事件是( )
至多有一次中靶
B.两次都中靶
C. 只有一次中靶
D. 两次都不中靶D5.把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁四人,每人分得一张,那么事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件
B.互斥但不对立事件
C.必然事件
D.不可能事件B运用新知P(C)=P(A∪B)= P(A)+P(B)=0.5, P(D)=1- P(C)=0.5. 6.如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方片(事件B)的概率是 ,问:
(l)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?运用新知运用新知7.袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,已知得到红球的概率是 ,得到黑球或黄球的概率是 ,得到黄球或绿球的概率也是 ,试求得到黑球、黄球、绿球的概率分别是多少?归纳总结概率的基本性质事件的关系与运算包含关系概率的基本性质相等关系并(和)事件交(积)事件互斥事件对立事件必然事件的概率为1不可能事件的概率为0概率的加法公式对立事件计算公式0≤P(A) ≤1作业:P121练习:1,2,3.
P124习题3.1 A组:5,6.
《学海》第3课时课后作业思考题 有人玩掷硬币走跳棋的游戏,已知硬币出现正反面为等可能性事件,棋盘上有第0站,第2站……第100站,一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面向上,棋子向前跳一站,(从K到K+1),若掷出反面向上,棋子向前跳两站(从K到K+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束,设棋子跳到第n站的概率为Pn.
(1)求P0,P1,P2的值.
(2)试寻找Pn,Pn-1,Pn-2三个概率的关系,其中n为整数,2≤n ≤99.
高中数学必修3第三章《概率》创设情境 我们可以把一次试验可能出现的结果看成一个集合(如连续抛掷两枚硬币),那么必然事件对应全集,随机事件对应子集,不可能事件对应空集,类比集合的关系与运算,事件之间存在怎样的关系与运算呢?1. 事件的关系与运算 在掷骰子试验中,我们用集合形式定义如下
事件:C1={出现1点},C2={出现2点},
C3={出现3点},C4={出现4点},
C5={出现5点},C6={出现6点},
D1={出现的点数不大于1},
D2={出现的点数大于4},
D3={出现的点数小于6},
E={出现的点数小于7},
F={出现的点数大于6},
G={出现的点数为偶数},
H={出现的点数为奇数}。如果事件C1发生,则一定有哪些事件发生?集合C1与这些集合之间的关系怎样描述? (1)一般地,对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或事件A包含于事件B),记作 B A ( 或A B ).②任何事件都包含不可能事件.①不可能事件用Ф表示;注意:分析事件C1={出现1点}
与事件D1={出现的点数不大于1},之间的包含关系,按集合观点这两
个事件之间的关系应怎样描述? (2)一般地,如果事件A发生,则事件B一定发生,反之也成立,这时称这两个事件相等,
记作:A=B . 若B A,且A B,则称事件A与事件B相等,记作A=B. 在掷骰子试验中,我们用集合形式定义如下事件:C1={出现1点},C2={出现2点}
C3={出现3点},C4={出现4点},
C5={出现5点},C6={出现6点},
D1={出现的点数不大于1},
D2={出现的点数大于4},
D3={出现的点数小于6},
E={出现的点数小于7},
F={出现的点数大于6},
G={出现的点数为偶数},
H={出现的点数为奇数},等等.如果事件C5发生或C6发生,就意味着哪个事件发生?反之成立吗? (3)当且仅当事件A发生或事件B发生时,事件C发生,则称事件C为事件A与事件B的并事件(或和事件),记作 C=A∪B(或A+B). 探究新知A∪BAB探究新知(4)当且仅当事件A发生且事件B发生时,事件C发生,则称事件C为事件A与事件B的交事件(或积事件),记作C=A∩B(或AB).A∩BAB探究新知(5)若A∩B为不可能事件(A∩B=Ф)此时,称事件A与事件B互斥.在一次试验中,事件A与事件B不能同时发生.含义:探究新知(6)若A∩B为不可能事件,A∪B为必然事件,则称事件A与事件B互为对立事件.若事件A与事件B不能同时发生,且事件A与事件B必有一个发生.含义:运用新知1.事件A与事件B的和事件、积事件,分别对应两个集合的并、交,那么事件A与事件B互为对立事件,对应的集合A、B是什么关系?集合A与集合B互为补集.2.给定下列命题,判断对错。(1)互斥事件一定对立;(2)对立事件一定互斥;3.一个射手进行一次射击,试判定下列
事件哪些是互斥事件?哪些是对立事件?(1)事件A:命中环数大于7;(2)事件B:命中环数为10环;(3)事件C:命中环数小于6;(4)事件D:命中环数为6、 7、8、9、10.事件C与事件D互斥且对立.事件A与事件C互斥,事件B与事件C互斥2.概率的几个基本性质(1)概率P(A)的取值范围②不可能事件C一定不发生, 则P(C)=0①必然事件B一定发生, 则 P(B)=1③随机事件A发生的概率为0<P(A)<1(2)概率的加法公式如果事件A与事件B互斥,则 P(A∪B)=P(A)+P(B).特别地,若事件A与事件B互为
对立事件,则P(A)+P(B)=1. 运用新知4.一个人打靶时连续射击两次事件“至少有一次中靶”的互斥事件是( )
至多有一次中靶
B.两次都中靶
C. 只有一次中靶
D. 两次都不中靶D5.把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁四人,每人分得一张,那么事件“甲分得红牌”与事件“乙分得红牌”是( )
A.对立事件
B.互斥但不对立事件
C.必然事件
D.不可能事件B运用新知P(C)=P(A∪B)= P(A)+P(B)=0.5, P(D)=1- P(C)=0.5. 6.如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方片(事件B)的概率是 ,问:
(l)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?运用新知运用新知7.袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,已知得到红球的概率是 ,得到黑球或黄球的概率是 ,得到黄球或绿球的概率也是 ,试求得到黑球、黄球、绿球的概率分别是多少?归纳总结概率的基本性质事件的关系与运算包含关系概率的基本性质相等关系并(和)事件交(积)事件互斥事件对立事件必然事件的概率为1不可能事件的概率为0概率的加法公式对立事件计算公式0≤P(A) ≤1作业:P121练习:1,2,3.
P124习题3.1 A组:5,6.
《学海》第3课时课后作业思考题 有人玩掷硬币走跳棋的游戏,已知硬币出现正反面为等可能性事件,棋盘上有第0站,第2站……第100站,一枚棋子开始在第0站,棋手每掷一次硬币,棋子向前跳动一次,若掷出正面向上,棋子向前跳一站,(从K到K+1),若掷出反面向上,棋子向前跳两站(从K到K+2),直到棋子跳到第99站(胜利大本营)或跳到第100站(失败集中营)时,该游戏结束,设棋子跳到第n站的概率为Pn.
(1)求P0,P1,P2的值.
(2)试寻找Pn,Pn-1,Pn-2三个概率的关系,其中n为整数,2≤n ≤99.
