高中数学必修1课件:3.2.2 函数模型的应用实例1(新人教A版)
文档属性
| 名称 | 高中数学必修1课件:3.2.2 函数模型的应用实例1(新人教A版) |  | |
| 格式 | rar | ||
| 文件大小 | 208.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-03-30 21:39:00 | ||
图片预览





文档简介
课件24张PPT。新人教A版 数学必修1 第三章 函数的应用3.2.2 函数模型的应用实例
(第一课时)
复习引入1、请同学们说说我们已经学过哪些函数模型? 一次函数、二次函数、指数函数、
对数函数以及幂函数等等.2、交流作业成果:请举出生活中函数模型的应用实例.实例分析 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2010 km,试建立行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象.
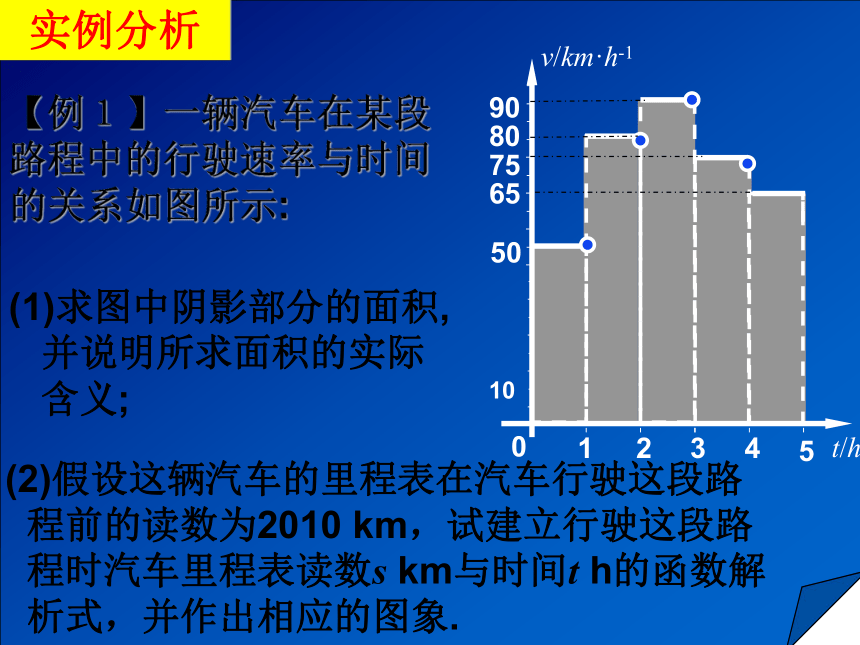
(1)求图中阴影部分的面积,并说明所求面积的实际含义;【例1】一辆汽车在某段路程中的行驶速率与时间的关系如图所示:实例分析t/h5v/km·h-165105075012348090路程(1)求图中阴影部分的面积,并说明所求面积的实际含义;
【例1】矩形面积=长×宽解:
(1)阴影部分的面积为 阴影部分的面积表示汽车在这5小时内行
驶的路程为360km.速率×时间=路程时
间速
率实例分析【例1】 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2010 km,试建立行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象.
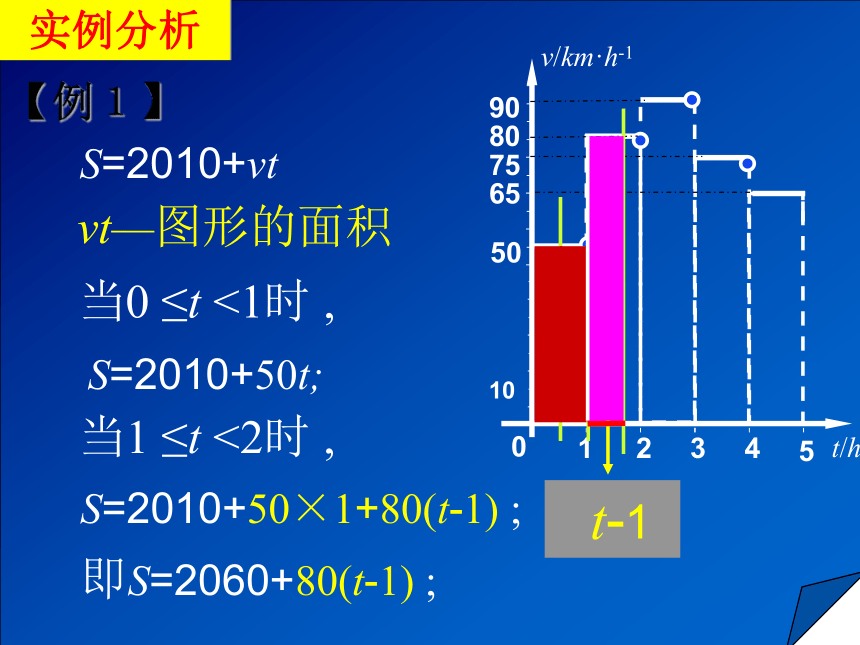
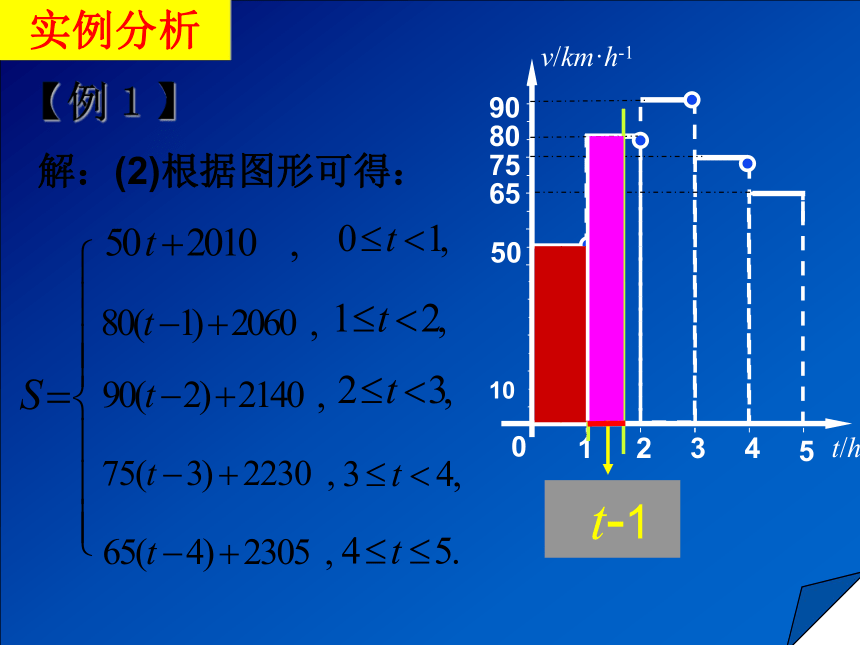
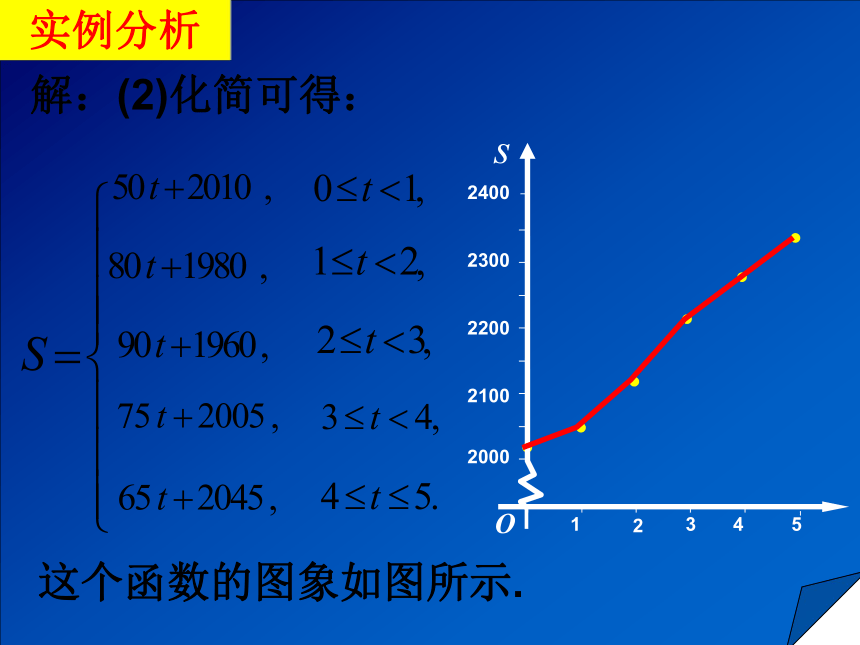
实例分析【例1】 t-1vt—图形的面积 S=2010+vt当0 ≤t <1时 ,S=2010+50t;当1 ≤t <2时 ,S=2010+50×1+80(t-1) ;即S=2060+80(t-1) ;实例分析【例1】解:(2)根据图形可得:解:(2)化简可得:这个函数的图象如图所示.实例分析 【例2 】某桶装水经营部每天的房租、人员工资
等固定成本为200元,每桶水的进价是5元,
销售单价与日均销售量的关系如下表所示: 请根据以上数据作出分析,这个经营部 怎样定价才能获得最大利润?实例分析②分析表格数据,日均销售量随销售单价的变化规律是什么?③当销售单价为x元/桶时,销售量为多少?④销售单价x受哪些条件的制约?条件:固定成本为200元,进价是5元/桶,任务:怎样定价才能获得最大利润?实例分析问题探究:①利润与哪些量有关?试用等式表示出来.【例2 】分析:①利润=日销售量×(售价-进价)-固定成本②销售单价每增加1元,日销售量就减少40桶③当销售单价为x元/桶时,日销售量为:
480-40(x-6)=720-40x(桶)④ x >5且720-40x >0. 因为销售单价每增加1元,日
均销售量就减少40桶,则日均销售量为:
480-40(x-6)=720-40x(桶).
由于x>5且720-40x>0, 即5<x<18, 所以
y=(720-40x)(x-5)-200
=-40x2+920x-3800 (5<x<18)
=-40(x - 11.5)2+1490.
所以,当x=11.5时,y有最大值. 故将销售单价
定为11.5元,就可获得最大的利润.实例分析【例2】解:设每桶水定价为x元时, 日均销
售利润为y元.因为销售单价每增加1元,日均销售量就减少40桶,则日均销售量为:
480-40(x-1)=520-40x(桶).
由于x>0且520-40x>0,即0<x<13,所以
y=(520-40x)x-200
=-40x2+520x-200(0<x<13)
=-40(x - 6.5 )2+1490
所以,当x=6.5时,y有最大值. 故将销售单价
定为11.5元,就可获得最大的利润.实例分析【例2】(解法二)
设在进价基础上增加x元后,日均销售利润为y元.反思归纳 建立(确定性)函数模型,解决实际问题的 一般程序是什么? 弄清题意,分清条件和结论,理顺数量关系; 求解数学模型,得出数学结论; 将文字语言、图表语言化为数学语言,利用数学知识,建立相应的数学模型; 将用数学知识和方法得出的结论,还原为实际问题的意义.①审题:②建模:③解模:④还原: 某支上市股票在30天内每股的日交易均价P(元)与时间t (天)组成有序数对(t,P), 且点(t,P)落在图中的两条线段上. 该股票在 30天内(含30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:反馈练习(1)写出这支股票每股的日交易均价P(元)与时间t (天)所满足的函数关系式; 解:(1) 当时,设由图象得 解得 即 同样的方法可求得当 时, 综上可得, 某支上市股票在30天内每股的日交易均价P(元)与时间t (天)组成有序数对(t,P), 且点(t,P)落在图中的两条线段上. 该股票在 30天内(含30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:反馈练习(2)根据表中数据确定日交易量Q(万股)与时间t (天)的一次函数关系式;反馈练习解:(2)设,由题意知:即,解得所以: 某支上市股票在30天内每股的日交易均价P(元)与时间t (天)组成有序数对(t,P), 且点(t,P)落在图中的两条线段上. 该股票在 30天内(含30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:反馈练习(3)求这30天中第几天的
日交易额最大,最大值为
多少万元?解:(3)设第t天的日交易额为f(t)万元,则
即解:(3)设第t 天的日交易额为f(t)万元,则
所以这30天中第15天的日交易额最大,
最大日交易额为125万元.课堂小结1、建立(确定)函数模型,解决实际问题的基本程序是什么? 实际问题数形结合、 2、在本节课的学习过程中,运用到了哪些
数学思想方法?课堂小结待定系数法、配方法.
化归与转化.分类与整合、作业布置必做题:教材P106练习第1题,
P107习题3.2A组第3,4题.
选做题: P108习题3.2B组第2题.再见 ! 祝各位同学
学习进步! 生活快乐!
(第一课时)
复习引入1、请同学们说说我们已经学过哪些函数模型? 一次函数、二次函数、指数函数、
对数函数以及幂函数等等.2、交流作业成果:请举出生活中函数模型的应用实例.实例分析 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2010 km,试建立行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象.
(1)求图中阴影部分的面积,并说明所求面积的实际含义;【例1】一辆汽车在某段路程中的行驶速率与时间的关系如图所示:实例分析t/h5v/km·h-165105075012348090路程(1)求图中阴影部分的面积,并说明所求面积的实际含义;
【例1】矩形面积=长×宽解:
(1)阴影部分的面积为 阴影部分的面积表示汽车在这5小时内行
驶的路程为360km.速率×时间=路程时
间速
率实例分析【例1】 (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2010 km,试建立行驶这段路程时汽车里程表读数s km与时间t h的函数解析式,并作出相应的图象.
实例分析【例1】 t-1vt—图形的面积 S=2010+vt当0 ≤t <1时 ,S=2010+50t;当1 ≤t <2时 ,S=2010+50×1+80(t-1) ;即S=2060+80(t-1) ;实例分析【例1】解:(2)根据图形可得:解:(2)化简可得:这个函数的图象如图所示.实例分析 【例2 】某桶装水经营部每天的房租、人员工资
等固定成本为200元,每桶水的进价是5元,
销售单价与日均销售量的关系如下表所示: 请根据以上数据作出分析,这个经营部 怎样定价才能获得最大利润?实例分析②分析表格数据,日均销售量随销售单价的变化规律是什么?③当销售单价为x元/桶时,销售量为多少?④销售单价x受哪些条件的制约?条件:固定成本为200元,进价是5元/桶,任务:怎样定价才能获得最大利润?实例分析问题探究:①利润与哪些量有关?试用等式表示出来.【例2 】分析:①利润=日销售量×(售价-进价)-固定成本②销售单价每增加1元,日销售量就减少40桶③当销售单价为x元/桶时,日销售量为:
480-40(x-6)=720-40x(桶)④ x >5且720-40x >0. 因为销售单价每增加1元,日
均销售量就减少40桶,则日均销售量为:
480-40(x-6)=720-40x(桶).
由于x>5且720-40x>0, 即5<x<18, 所以
y=(720-40x)(x-5)-200
=-40x2+920x-3800 (5<x<18)
=-40(x - 11.5)2+1490.
所以,当x=11.5时,y有最大值. 故将销售单价
定为11.5元,就可获得最大的利润.实例分析【例2】解:设每桶水定价为x元时, 日均销
售利润为y元.因为销售单价每增加1元,日均销售量就减少40桶,则日均销售量为:
480-40(x-1)=520-40x(桶).
由于x>0且520-40x>0,即0<x<13,所以
y=(520-40x)x-200
=-40x2+520x-200(0<x<13)
=-40(x - 6.5 )2+1490
所以,当x=6.5时,y有最大值. 故将销售单价
定为11.5元,就可获得最大的利润.实例分析【例2】(解法二)
设在进价基础上增加x元后,日均销售利润为y元.反思归纳 建立(确定性)函数模型,解决实际问题的 一般程序是什么? 弄清题意,分清条件和结论,理顺数量关系; 求解数学模型,得出数学结论; 将文字语言、图表语言化为数学语言,利用数学知识,建立相应的数学模型; 将用数学知识和方法得出的结论,还原为实际问题的意义.①审题:②建模:③解模:④还原: 某支上市股票在30天内每股的日交易均价P(元)与时间t (天)组成有序数对(t,P), 且点(t,P)落在图中的两条线段上. 该股票在 30天内(含30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:反馈练习(1)写出这支股票每股的日交易均价P(元)与时间t (天)所满足的函数关系式; 解:(1) 当时,设由图象得 解得 即 同样的方法可求得当 时, 综上可得, 某支上市股票在30天内每股的日交易均价P(元)与时间t (天)组成有序数对(t,P), 且点(t,P)落在图中的两条线段上. 该股票在 30天内(含30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:反馈练习(2)根据表中数据确定日交易量Q(万股)与时间t (天)的一次函数关系式;反馈练习解:(2)设,由题意知:即,解得所以: 某支上市股票在30天内每股的日交易均价P(元)与时间t (天)组成有序数对(t,P), 且点(t,P)落在图中的两条线段上. 该股票在 30天内(含30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示:反馈练习(3)求这30天中第几天的
日交易额最大,最大值为
多少万元?解:(3)设第t天的日交易额为f(t)万元,则
即解:(3)设第t 天的日交易额为f(t)万元,则
所以这30天中第15天的日交易额最大,
最大日交易额为125万元.课堂小结1、建立(确定)函数模型,解决实际问题的基本程序是什么? 实际问题数形结合、 2、在本节课的学习过程中,运用到了哪些
数学思想方法?课堂小结待定系数法、配方法.
化归与转化.分类与整合、作业布置必做题:教材P106练习第1题,
P107习题3.2A组第3,4题.
选做题: P108习题3.2B组第2题.再见 ! 祝各位同学
学习进步! 生活快乐!
