等比数列的前n项和
图片预览




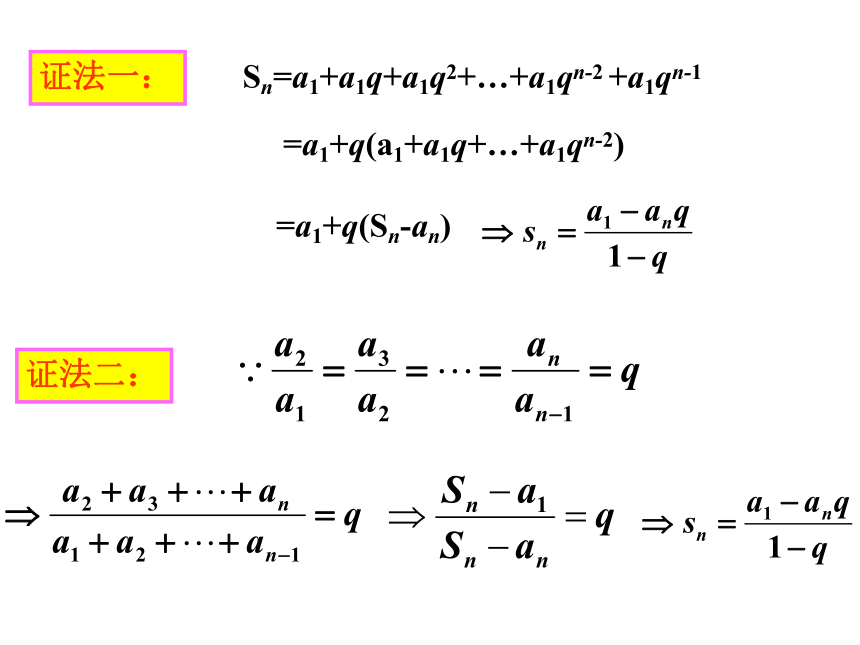
文档简介
课件16张PPT。等比数列的前n项和?分析:这首古诗前三句给大家展现了
一幅美丽的夜景,最后一句把它变成了一个数学问题,你能用今天的知识求出这首古诗的答案吗? 相传,古印度的舍罕王打算重赏国际象棋的发明者
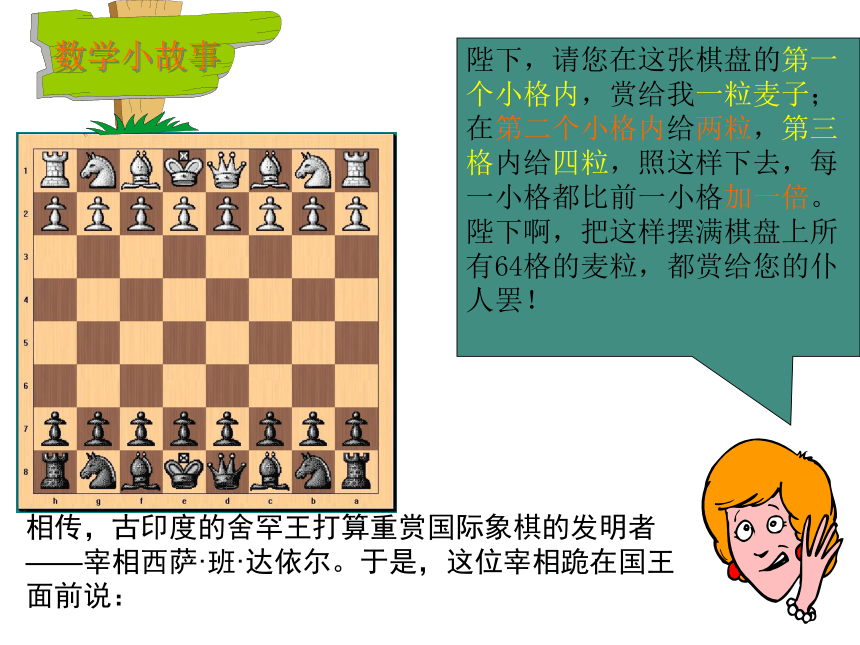
——宰相西萨·班·达依尔。于是,这位宰相跪在国王
面前说:陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子;在第二个小格内给两粒,第三格内给四粒,照这样下去,每一小格都比前一小格加一倍。
陛下啊,把这样摆满棋盘上所
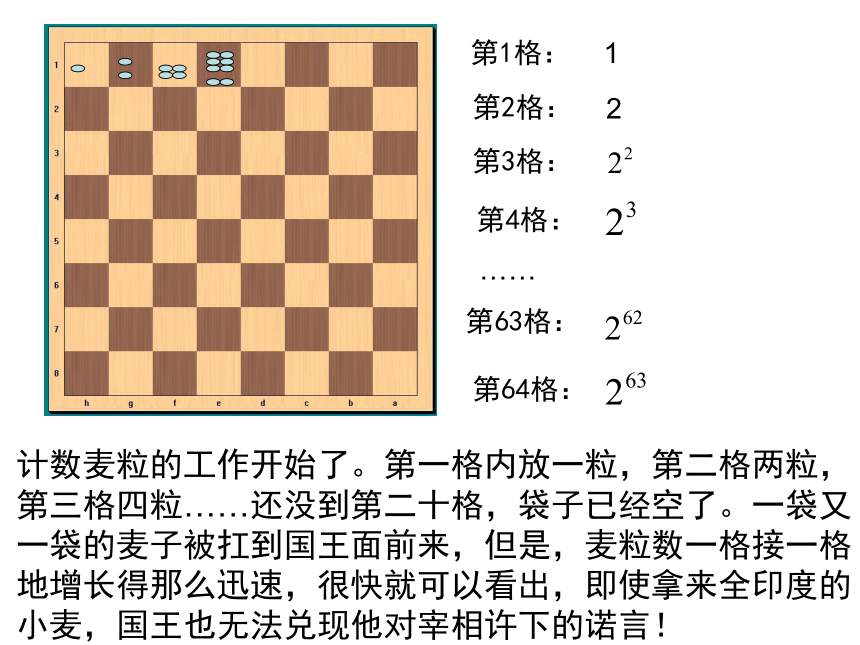
有64格的麦粒,都赏给您的仆人罢!数学小故事计数麦粒的工作开始了。第一格内放一粒,第二格两粒,第三格四粒……还没到第二十格,袋子已经空了。一袋又一袋的麦子被扛到国王面前来,但是,麦粒数一格接一格地增长得那么迅速,很快就可以看出,即使拿来全印度的小麦,国王也无法兑现他对宰相许下的诺言! 第1格:第2格:第4格:第3格:第63格:第64格:12……这位聪明的宰相到底要求的是多少麦粒呢?这实际上是求1为首项,2为公比的等比数列的前64项的和。=18,446,744,073,709,551,615 ?说明: 超过了1 .84 ,假定千粒麦子的质量为 40g,那么麦粒的总质量超过了7000亿吨,相当全世界在两千年内所产的小麦的总和!如果造一个宽四米,高四米的粮仓来储存这些粮食,那么这个粮仓就要长三亿千米,可以绕地球赤道7500圈,或在太阳和地球之间打个来回。所以国王是不可能满足发明者的要求。 ⑴-⑵,得由此得q≠1时,设等比数列它的前n项和是等比数列前n项和公式的推导:错位相减法证法一:Sn=a1+a1q+a1q2+…+a1qn-2 +a1qn-1 =a1+q(a1+a1q+…+a1qn-2)=a1+q(Sn-an)证法二:(1) 和 各已知三个可求第四个。 等比数列的前n项和表述为:例2某商场今年销售计算机5000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今起,大约几年可使总销售量达到30000台(结果保留到个位)?分析:第1年产量为 5000台第2年产量为 5000×(1+10%)=5000×1.1台第3年产量为5000×(1+10%) ×(1+10%)则n年内的总产量为:
解:由题意,从第1年起,每年的销售量组成一个等比数列其中∴即两边取常用
对数,得 例2某商场今年销售计算机5000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今起,大约几年可使总销售量达到30000台(结果保留到个位)??分析:这首古诗前三句给大家展现了
一幅美丽的夜景,最后一句把它变成了一个数学问题,你能用今天的知识求出这首古诗的答案吗? 等差数列 {an}等比数列 {an}定义an+1 - an = d ( 常数 )an+1 / an = q ( 不为零的常数 )通项 an = a1 + ( n – 1 ) d an - am = ( n – m ) d an = a1 qn-1 an / am = qn-m⑴公式⑵推导
方法①归纳猜想验证法②首尾相咬累加法①归纳猜想验证法②首尾相咬累乘法性质若 m+n=p+q , m、n、p、q∈N*则 am + an = ap + aq则 am · an = ap · aq前n项和Sn⑴公式⑵推导
方法若 m+n=p+q , m、n、p、q∈N* = na1 +倒序相加1、等比数列前n项和:小 结错位相减法2、注意选择适当的公式,必要是分情况讨论。3、学会建立等比数列的数学模型,来解决
实际问题。本节课你学习到了新知道识,要努力哦!努力才能放飞你的梦想!
一幅美丽的夜景,最后一句把它变成了一个数学问题,你能用今天的知识求出这首古诗的答案吗? 相传,古印度的舍罕王打算重赏国际象棋的发明者
——宰相西萨·班·达依尔。于是,这位宰相跪在国王
面前说:陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子;在第二个小格内给两粒,第三格内给四粒,照这样下去,每一小格都比前一小格加一倍。
陛下啊,把这样摆满棋盘上所
有64格的麦粒,都赏给您的仆人罢!数学小故事计数麦粒的工作开始了。第一格内放一粒,第二格两粒,第三格四粒……还没到第二十格,袋子已经空了。一袋又一袋的麦子被扛到国王面前来,但是,麦粒数一格接一格地增长得那么迅速,很快就可以看出,即使拿来全印度的小麦,国王也无法兑现他对宰相许下的诺言! 第1格:第2格:第4格:第3格:第63格:第64格:12……这位聪明的宰相到底要求的是多少麦粒呢?这实际上是求1为首项,2为公比的等比数列的前64项的和。=18,446,744,073,709,551,615 ?说明: 超过了1 .84 ,假定千粒麦子的质量为 40g,那么麦粒的总质量超过了7000亿吨,相当全世界在两千年内所产的小麦的总和!如果造一个宽四米,高四米的粮仓来储存这些粮食,那么这个粮仓就要长三亿千米,可以绕地球赤道7500圈,或在太阳和地球之间打个来回。所以国王是不可能满足发明者的要求。 ⑴-⑵,得由此得q≠1时,设等比数列它的前n项和是等比数列前n项和公式的推导:错位相减法证法一:Sn=a1+a1q+a1q2+…+a1qn-2 +a1qn-1 =a1+q(a1+a1q+…+a1qn-2)=a1+q(Sn-an)证法二:(1) 和 各已知三个可求第四个。 等比数列的前n项和表述为:例2某商场今年销售计算机5000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今起,大约几年可使总销售量达到30000台(结果保留到个位)?分析:第1年产量为 5000台第2年产量为 5000×(1+10%)=5000×1.1台第3年产量为5000×(1+10%) ×(1+10%)则n年内的总产量为:
解:由题意,从第1年起,每年的销售量组成一个等比数列其中∴即两边取常用
对数,得 例2某商场今年销售计算机5000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今起,大约几年可使总销售量达到30000台(结果保留到个位)??分析:这首古诗前三句给大家展现了
一幅美丽的夜景,最后一句把它变成了一个数学问题,你能用今天的知识求出这首古诗的答案吗? 等差数列 {an}等比数列 {an}定义an+1 - an = d ( 常数 )an+1 / an = q ( 不为零的常数 )通项 an = a1 + ( n – 1 ) d an - am = ( n – m ) d an = a1 qn-1 an / am = qn-m⑴公式⑵推导
方法①归纳猜想验证法②首尾相咬累加法①归纳猜想验证法②首尾相咬累乘法性质若 m+n=p+q , m、n、p、q∈N*则 am + an = ap + aq则 am · an = ap · aq前n项和Sn⑴公式⑵推导
方法若 m+n=p+q , m、n、p、q∈N* = na1 +倒序相加1、等比数列前n项和:小 结错位相减法2、注意选择适当的公式,必要是分情况讨论。3、学会建立等比数列的数学模型,来解决
实际问题。本节课你学习到了新知道识,要努力哦!努力才能放飞你的梦想!
