等比数列性质

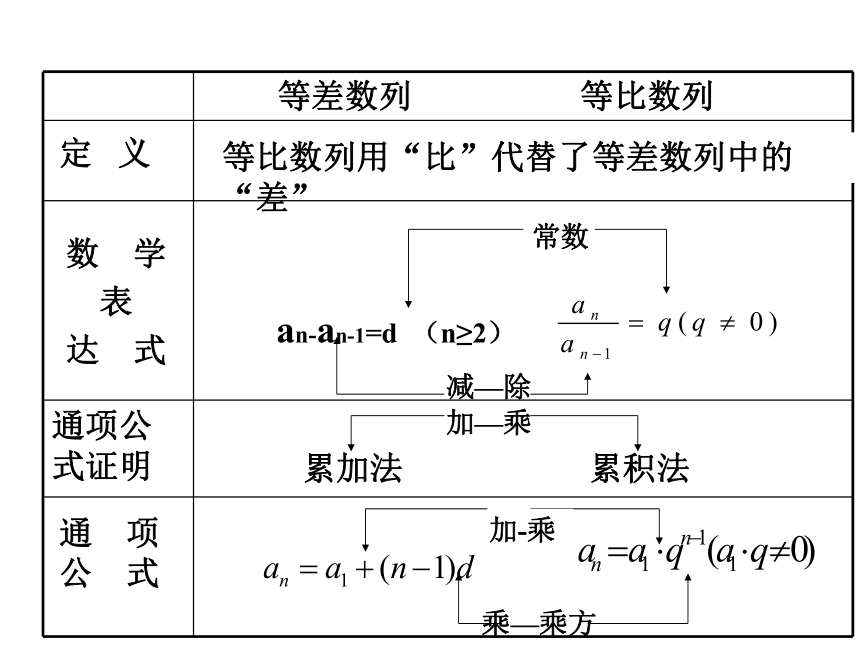
课件10张PPT。Welcome to our classroom2010年3月15日常数减—除加—乘加-乘
乘—乘方 累加法累积法等比数列用“比”代替了等差数列中的“差”定 义
数 学
表
达 式通项公式证明
通 项 公 式an-an-1=d （n≥2）
通过观察，我们发现： 等差数列中的减法、加法、乘法， 在等比数列中升级为除法、乘法、乘方. 练习:⒈在等差数列{an}中，a2=-2,a5=54，求a8=_____.
⒉在等差数列{an}中，若a3+a4+a5+a6+a7=450，则a2+a8的值为_________.
⒊在等差数列{an}中， a15 =10, a45=90,则 a60 =__________.

⒋在等差数列{an}中，a1+a2 =30, a3+a4 =120, 则a5+a6=_____ .
110运用性质： an=am+(n-m)d或等差中项运用性质： 若n+m=p+q则am+an=ap+aq
运用性质：从原数列中取出偶数项组成的新数列公差为2d.(可推广)
运用性质：若{an}是公差为d的等差数列 {cn}是公差为d′的等差数列，则数列{an+cn}是公差为d+d′的等差数列。180130210由等差数列的性质，猜想等比数列的性质猜想1： 若bn-k,bn,bn+k
是{bn}中的三项
则
猜想3：若n+m=p+q
则bn·bm=bp·bq
由等差数列的性质，猜想等比数列的性质猜想４：从原数列中取出偶数项，组成的新数列公比为 .
(可推广)
猜想５：若{dn}是公比为q′的等比数列,则数列{bn?dn}是公比为q·q′的等比数列.
试试看 ⒈在等比数列{an}中，a2=-2,a5=54，a8= .
⒉在等比数列{an}中，且an＞0，
a2 a4+2a3a5+a4a6=36,那么a3+a5= _ .
⒊在等比数列{an}中， a15 =10, a45=90,则 a60 =__________.
⒋在等比数列{an}中，a1+a2 =30, a3+a4 =120, 则a5+a6=_____ .
思考：
在等比数列{an}中，a1+a2 =30, a3+a4 =120, 则a5+a6=_____ .
-14586270480480或-270解题技巧的类比应用：三个数成等比数列，它们的和等于14，它们的积等于64.求这三个数。 分析：若三个数成等差数列，则设这三个数
为a-d,a,a+d.由类比思想的应用可得，
若三个数成等比数列，则设这三个数
为：，

a,a ? q.再由方程组可得：q=2 或既这三个数为2，4，8或8，4，2。
再 见