9.4解直角三角形学案1

9.4解直角三角形学案
山东省单县终兴中学 编写人 王敏 吴新峰 审阅人 吴吉杰
一 学习目标：
1理解解直角三角形的概念，会选择正确的方法解直角三角形。
2能运用锐角三角比解直角三角形。
二知识回顾：
在Rt△ABC中，∠C＝900，a，b，c，分别为∠A,∠B,∠C所对的边，
则边之间的关系为 ，角之间的关系为 ，
角与边之间的关系为 ，
三自主预习：
1解直角三角的概念：
有直角三角形中 求出 元素的过程，叫做解直角三角形。
2解直角三角形的两种情况。
（1）已知 ，求第三边及两锐角。
（2）已知 和一个 ，求其它两边及另一锐角。
四 导学探究：
在Rr△ABC中，共有六个量，三条边a，b，c，三个角∠A，∠B，∠C，其中∠C是已知的，其它的五个量都是未知的。
（1） 已知∠A，∠B，能求出其它的三个量a，b，c吗？
（2） 已知两条边的长，能求出其它的三个量吗？
（3） 已知一角和一边，能求出其它的三个量吗？
你有什么发现？
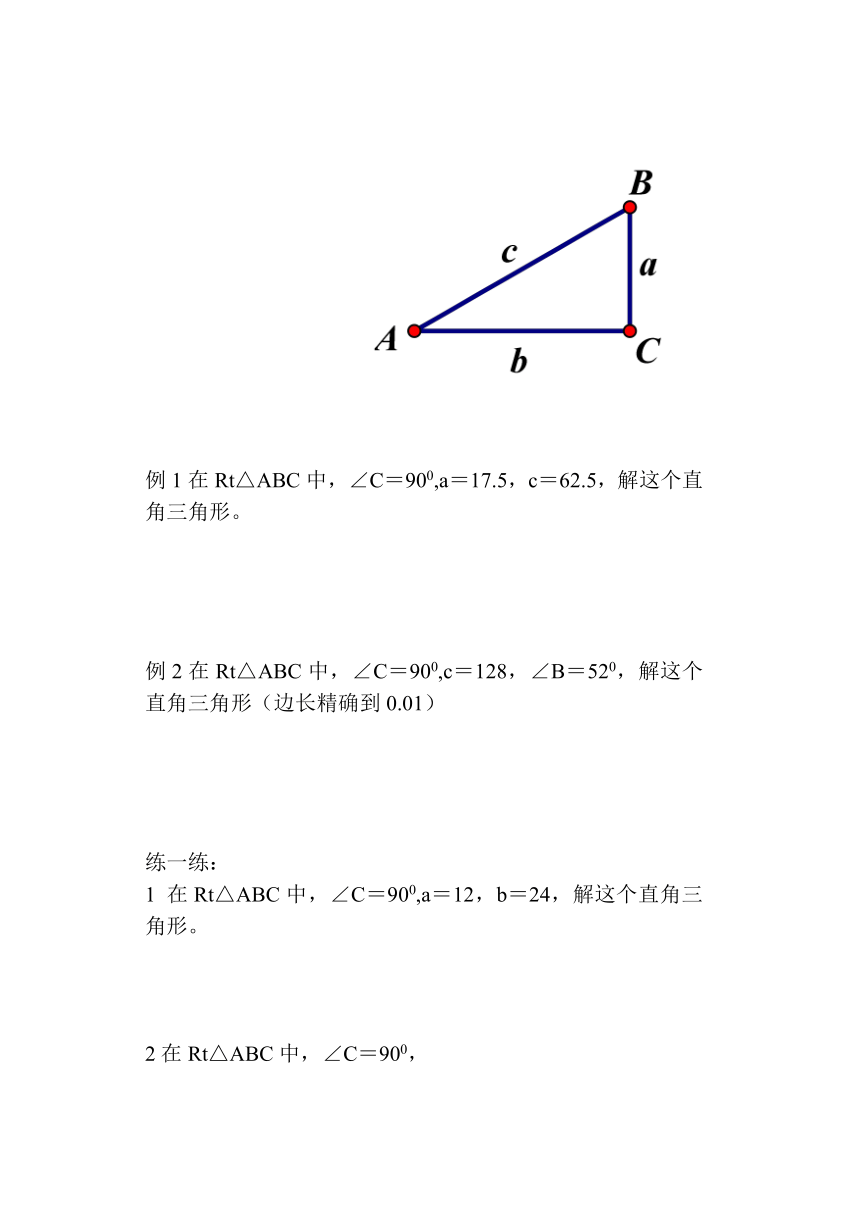
例1在Rt△ABC中，∠C＝900,a＝17.5，c＝62.5，解这个直角三角形。
例2在Rt△ABC中，∠C＝900,c＝128，∠B＝520，解这个直角三角形（边长精确到0.01）
练一练：
1 在Rt△ABC中，∠C＝900,a＝12，b＝24，解这个直角三角形。
2在Rt△ABC中，∠C＝900，
（1） 已知c＝15，∠B＝600，求a；
（2） 已知∠A＝350，a＝24，求b，c
五 当堂达标；
1在Rt△ABC中，∠C＝900，BC＝a，AC＝b，且3 a＝4b，则∠A的度数是 （ ）
A 53.70 B 53.130 C 53013′ D 53048′
2已知Rt△ABC中，∠C＝900，∠A＝300，斜边上的高为1，则△ABC三边的长分别为（ ）
A a＝2 ，b＝2， c＝4，
B a＝， b＝2， c ＝
C a＝，b＝2，c＝，
D a＝2,b＝,c＝
2已知在Rt△ABC中，∠C＝900，a，b，c，分别为∠A,∠B,∠C所对的边，由下列条件解直角三角形。
（1）已知a＝6，b＝6，求c，
（2）已知a＝20,c＝20，求∠B；
（3）已知c＝30，∠A,600，求a；
六 课后提升
3 如图，已知Rt⊿ABC中，斜边BC上的高AD=4，cosB=,则AC=
4 如图，⊿ABC中，∠C=900，∠B=300，AD是⊿ABC的角平分线，若AC=,求线段AD的长。