抛物线几何性质
图片预览






文档简介
课件21张PPT。2.3.2抛物线的简单几何性质1、抛物线的定义: 我们把平面内与一个定点 和一条定直线 的距离相等的点的轨迹叫做抛物线,点 叫做抛物线的焦点,直线 叫做抛物线的准线.复习与巩固: 你还知道抛物线的标准方程
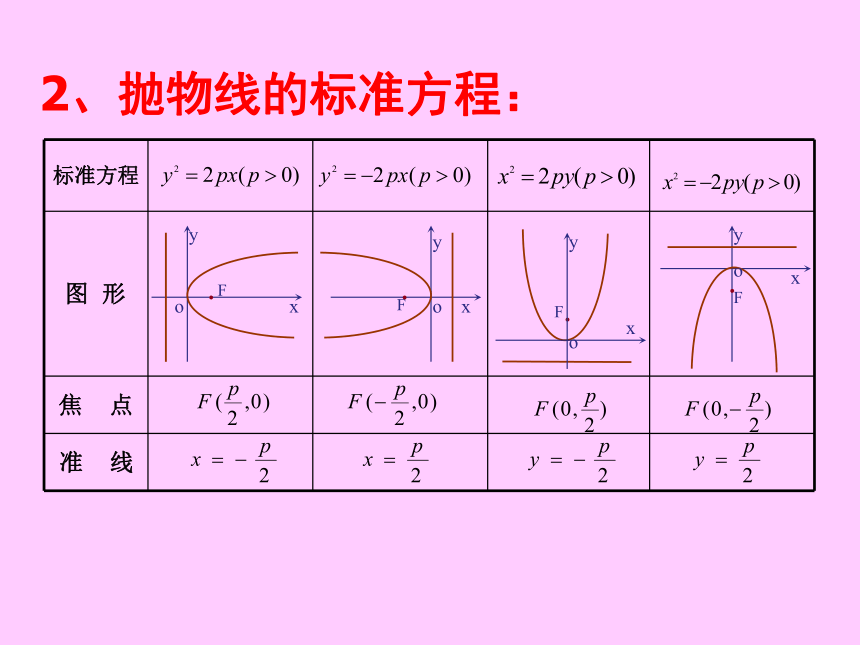
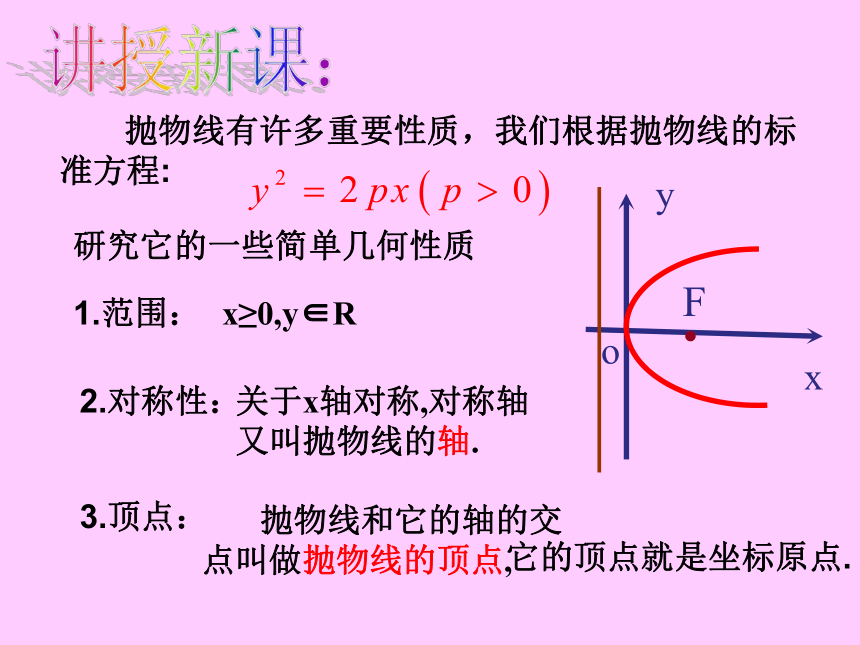
还有哪些不同的形式吗?2、抛物线的标准方程:x≥0,y∈R关于x轴对称,对称轴又叫抛物线的轴.讲授新课:1.范围:2.对称性:3.顶点:e=1|PF|=x0+p/2通径的长度:2P4.离心率:抛物线上的点M到焦点的距离和它到准线的距离之比,叫做抛物线的离心率.用e表示:5.焦半径:6.通径:其他各种形式类比可得,见下表:y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的e=1;5.抛物线标准方程中的p对抛物线开口的影响. P越大,开口越开阔.特别注意:例题讲解: 例1. 已知抛物线关于 轴对称,它的顶点在坐标原点, 并且过点M ,求它的标准方程. 想一想方法探究:具体步骤有同学们给出.答案:变式练习:答:这时,直线 与抛物线只有一个公共点.解得 于是,当 且 时,方程(Ⅰ)有2
个解,从而,方程组(Ⅰ)有两个解,这时,直线
与抛物线有2个公共点.③由 即解得 于是,当 时,方程没有实数解,从而方程组(Ⅰ)没有解,这时,直线 与抛物线没有公共点.综上可得: 当 时 ,直线 与抛物线只有一个公共点;
当 时,直线 与抛物线有两个公共点; 当 时,直线 与抛物线没有公共点.判断直线与抛物线位置关系的操作程序:把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
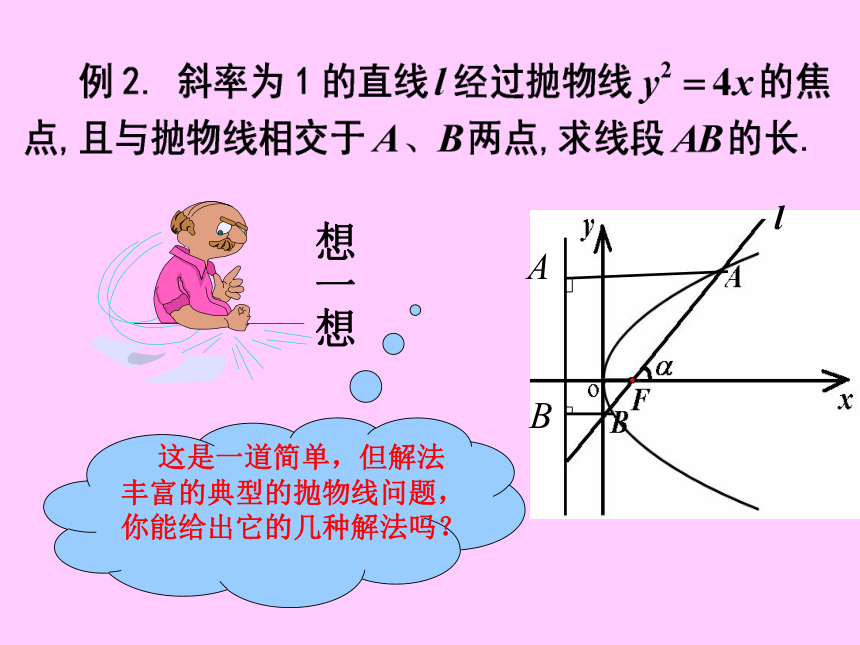
对称轴平行相交(一个交点) 计 算 判 别 式总结:巩固与练习: 1)过抛物线 的焦点,作倾斜角为 的直线,则被抛物线截得的弦长为 ; 3)抛物线 上的点到直线
的距离的最小值是( )16 下面是最近两年几个省份的高考试题,请同学们做一下看看你的实力吧. 1.(2009年山东卷(文)10)设斜率为2的直线
过抛物线 的焦点 ,且和 轴交于点 若 的面积为4,则抛物线方程为( ) A 高考欣赏:A 3.(2008年山东卷(理)22)如图,设抛物线方程为
为直线 上任意一点,过 引抛物线的切线,切点
分别为 (1)求证: 三点的横坐标成等差数列; (2)已知当 点的坐标为 时,
求此时抛物线的方程; (3)是否存在点 ,使得点C关直线 的对称点 在抛物线
上,其中,点C满足
( 为坐标原点),若存在,求出所有适合题意的点 的坐标;若不存在,请说明理由。(1)略;(2)(3)仅存在一点 适合题意再见谢谢收看
还有哪些不同的形式吗?2、抛物线的标准方程:x≥0,y∈R关于x轴对称,对称轴又叫抛物线的轴.讲授新课:1.范围:2.对称性:3.顶点:e=1|PF|=x0+p/2通径的长度:2P4.离心率:抛物线上的点M到焦点的距离和它到准线的距离之比,叫做抛物线的离心率.用e表示:5.焦半径:6.通径:其他各种形式类比可得,见下表:y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)关于x轴对称 关于x轴对称 关于y轴对称 关于y轴对称(0,0)(0,0)(0,0)(0,0)1.抛物线只位于半个坐标平面内,虽然它可以无限延伸,但它没有渐近线;2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的e=1;5.抛物线标准方程中的p对抛物线开口的影响. P越大,开口越开阔.特别注意:例题讲解: 例1. 已知抛物线关于 轴对称,它的顶点在坐标原点, 并且过点M ,求它的标准方程. 想一想方法探究:具体步骤有同学们给出.答案:变式练习:答:这时,直线 与抛物线只有一个公共点.解得 于是,当 且 时,方程(Ⅰ)有2
个解,从而,方程组(Ⅰ)有两个解,这时,直线
与抛物线有2个公共点.③由 即解得 于是,当 时,方程没有实数解,从而方程组(Ⅰ)没有解,这时,直线 与抛物线没有公共点.综上可得: 当 时 ,直线 与抛物线只有一个公共点;
当 时,直线 与抛物线有两个公共点; 当 时,直线 与抛物线没有公共点.判断直线与抛物线位置关系的操作程序:把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线的
对称轴平行相交(一个交点) 计 算 判 别 式总结:巩固与练习: 1)过抛物线 的焦点,作倾斜角为 的直线,则被抛物线截得的弦长为 ; 3)抛物线 上的点到直线
的距离的最小值是( )16 下面是最近两年几个省份的高考试题,请同学们做一下看看你的实力吧. 1.(2009年山东卷(文)10)设斜率为2的直线
过抛物线 的焦点 ,且和 轴交于点 若 的面积为4,则抛物线方程为( ) A 高考欣赏:A 3.(2008年山东卷(理)22)如图,设抛物线方程为
为直线 上任意一点,过 引抛物线的切线,切点
分别为 (1)求证: 三点的横坐标成等差数列; (2)已知当 点的坐标为 时,
求此时抛物线的方程; (3)是否存在点 ,使得点C关直线 的对称点 在抛物线
上,其中,点C满足
( 为坐标原点),若存在,求出所有适合题意的点 的坐标;若不存在,请说明理由。(1)略;(2)(3)仅存在一点 适合题意再见谢谢收看
