2.2 平面向量的线性运算
图片预览










文档简介
课件40张PPT。2.2 平面向量的线性运算 2.运算性质
a+b=b+a(交换律);
(a+b)+c=a+(b+c)(结合律);
a+0=0+a=a.
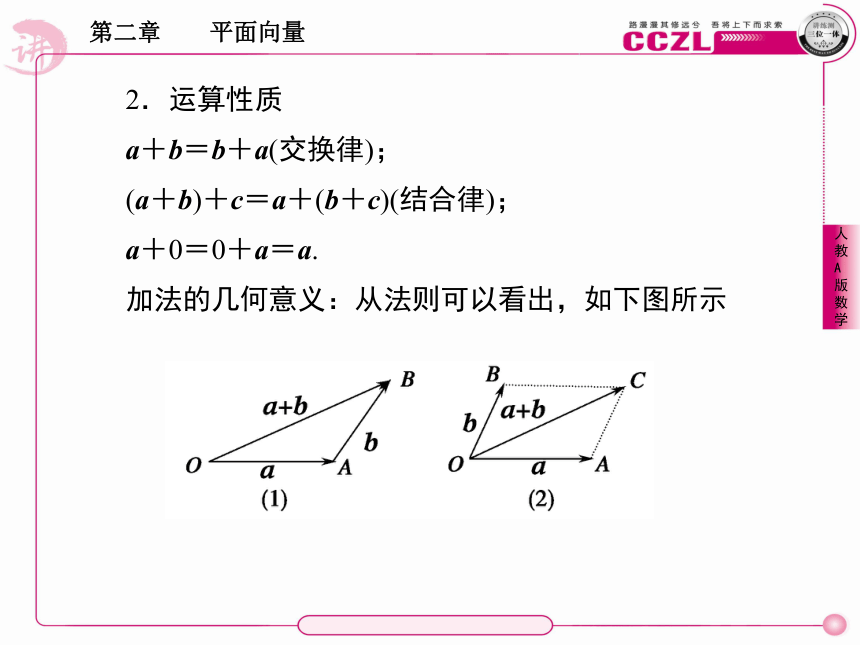
加法的几何意义:从法则可以看出,如下图所示3.向量加法的模
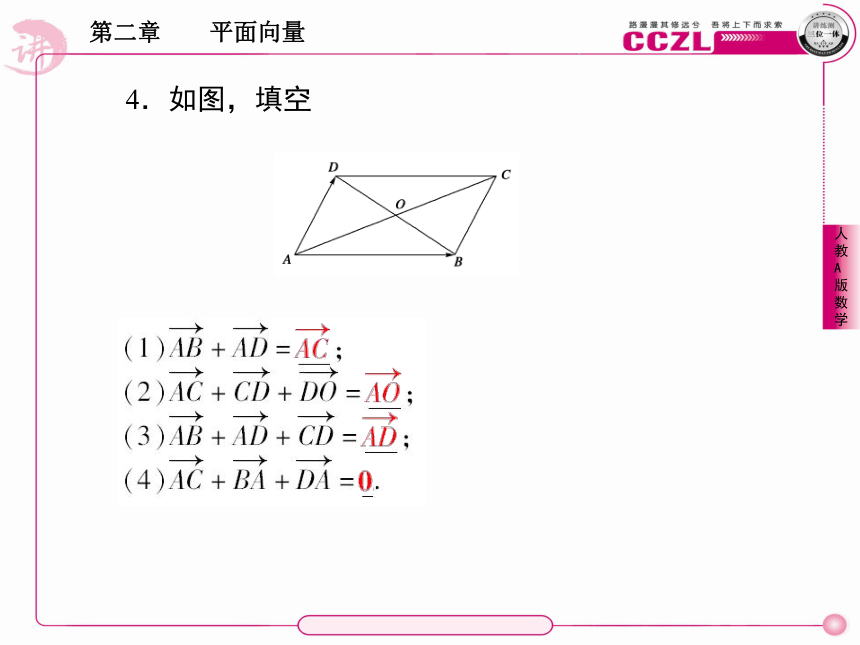
对于两个共线向量a,b,当a与b方向相同时,向量a+b与向量a的方向相同,且|a+b|= .当a与b方向相反时,若|a|>|b|,则向量a+b与 的方向相同,且|a+b|= ;若|a|<|b|,则向量a+b与 的方向相同,且|a+b|= .一般地,|a+b|≤|a|+|b|,当a与b方向 时,取等号.|a|+|b|a|a|-|b|b|b|-|a|相同4.如图,填空重点:向量加法运算及其几何意义.
难点:对向量加法法则的理解和应用.1.应注意向量相加与向量的模相加的区别,两向量的和仍然是一个向量.
2.向量和的三角形法则对所有向量都适用,但平行四边形法则在两向量共线时不适用.
[例1] 如下图中(1)、(2)所示,试作出向量a与b的和.
[分析] 依据向量加法的三角形法则,在平面上任取一点O,以O为起点作出一个向量等于a,再以终点为起点作下一个向量等于b,可得出a+b.[解析] 如下图中(1)、(2)所示,
(1)如图,已知a、b,求作a+b.
(2)如图所示,已知向量a、b、c,求作和向量a+b+c.[解析] (1)[答案] (1)2a+b,2a+2b,a+2b (2)0
[解析] (1)如图,连结FC交AD于点O,连结OB,由平面几何知识得四边形ABOF,四边形ABCO均为平行四边形.
[例3] 证明:对角线互相平分的四边形是平行四边形.[点评] 用向量解决平面几何问题,关键是将所要解决的问题和已知条件向量化,然后通过向量知识加以解决.
[例4] 在小船过河时,小船沿垂直河岸方向行驶,速度为v1=3.46km/h,河水流动的速度v2=2.0km/h,试求小船过河实际行驶速度的大小和方向.[例5] 试证,对于任意给定向量a,b,均有||a|-|b||≤|a+b|≤|a|+|b|.[辨析] 错解没有考虑a、b的所有可能情形,只就a与b不共线时,用三角形的性质得出结论.以偏概全致误.一、选择题
1.下列等式中不正确的是
( )
A.a+0=a
B.a+b=b+a
C.|a+b|=|a|+|b|
[答案] C
[解析] 当a与b方向不同时,|a+b|≠|a|+|b|.[答案] B [答案] D [答案] D
a+b=b+a(交换律);
(a+b)+c=a+(b+c)(结合律);
a+0=0+a=a.
加法的几何意义:从法则可以看出,如下图所示3.向量加法的模
对于两个共线向量a,b,当a与b方向相同时,向量a+b与向量a的方向相同,且|a+b|= .当a与b方向相反时,若|a|>|b|,则向量a+b与 的方向相同,且|a+b|= ;若|a|<|b|,则向量a+b与 的方向相同,且|a+b|= .一般地,|a+b|≤|a|+|b|,当a与b方向 时,取等号.|a|+|b|a|a|-|b|b|b|-|a|相同4.如图,填空重点:向量加法运算及其几何意义.
难点:对向量加法法则的理解和应用.1.应注意向量相加与向量的模相加的区别,两向量的和仍然是一个向量.
2.向量和的三角形法则对所有向量都适用,但平行四边形法则在两向量共线时不适用.
[例1] 如下图中(1)、(2)所示,试作出向量a与b的和.
[分析] 依据向量加法的三角形法则,在平面上任取一点O,以O为起点作出一个向量等于a,再以终点为起点作下一个向量等于b,可得出a+b.[解析] 如下图中(1)、(2)所示,
(1)如图,已知a、b,求作a+b.
(2)如图所示,已知向量a、b、c,求作和向量a+b+c.[解析] (1)[答案] (1)2a+b,2a+2b,a+2b (2)0
[解析] (1)如图,连结FC交AD于点O,连结OB,由平面几何知识得四边形ABOF,四边形ABCO均为平行四边形.
[例3] 证明:对角线互相平分的四边形是平行四边形.[点评] 用向量解决平面几何问题,关键是将所要解决的问题和已知条件向量化,然后通过向量知识加以解决.
[例4] 在小船过河时,小船沿垂直河岸方向行驶,速度为v1=3.46km/h,河水流动的速度v2=2.0km/h,试求小船过河实际行驶速度的大小和方向.[例5] 试证,对于任意给定向量a,b,均有||a|-|b||≤|a+b|≤|a|+|b|.[辨析] 错解没有考虑a、b的所有可能情形,只就a与b不共线时,用三角形的性质得出结论.以偏概全致误.一、选择题
1.下列等式中不正确的是
( )
A.a+0=a
B.a+b=b+a
C.|a+b|=|a|+|b|
[答案] C
[解析] 当a与b方向不同时,|a+b|≠|a|+|b|.[答案] B [答案] D [答案] D
