向量减法、数乘及几何意义
图片预览








文档简介
课件51张PPT。1.相反向量
我们规定,与a长度 ,方向 的向量,叫做a的相反向量,记作-a,零向量的相反向量仍是 .
关于相反向量有以下结论
①-(-a)= ;
②a+(-a)=(-a)+a= ;
③若a、b是互为相反的向量,则b=-a,a+b= .相等相反零向量a002.向量减法
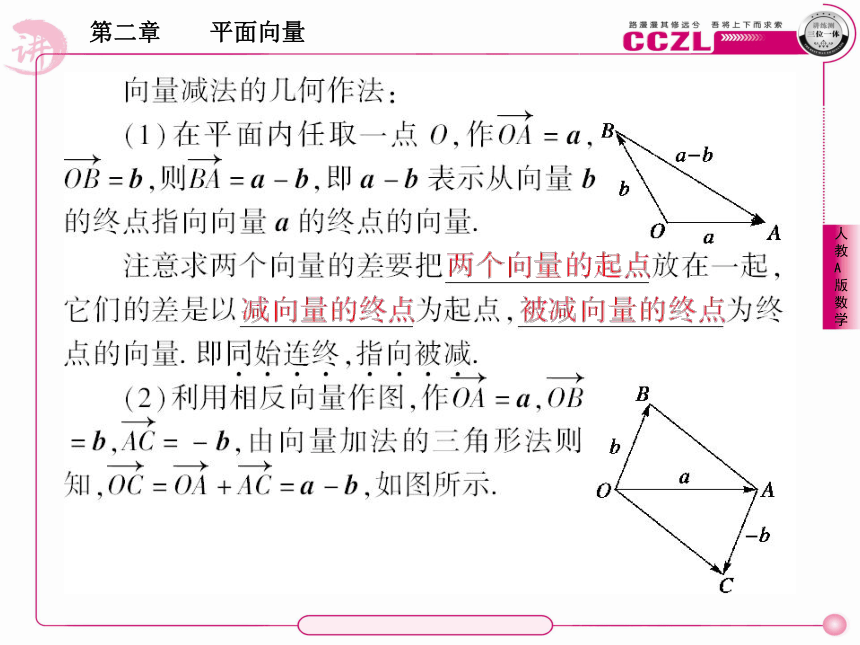
(1)定义
我们定义a-b=a+ ,即减去一个向量等于加上这个向量的 .
(2)向量减法的作图
因为(a-b)+b=a+[(-b)+b]=a+0=a,所以求a-b就是求这样一个向量,它与b的和等于a,从而得到a-b的作图法.相反向量(-b)3.向量数乘
一般地,我们规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作λa.它的长度及方向规定如下:
(1)|λa|= ;
(2)λ>0时,λa的方向与a的方向 ;λ<0时,λa的方向与a的方向 ;
(3)当λ=0时,λa= .
注意向量数乘的结果仍是一个向量.
向量数乘满足下列运算律,设λ、μ为实数|λ|·|a|相同相反0(1)λ(μa)= .
(2)(λ+μ)a= .
(3)λ(a+b)= .
向量的加、减、数乘运算统称为 .
向量数乘的几何意义
向量数乘的几何意义就是把 .当λ>0时,沿着a的方向扩大(λ>1)或缩小(0<λ<1)λ倍;当λ<0时,沿着a的反方向扩大(|λ|>1)或缩小(|λ|<1)|λ|倍.λuaλa+μaλa+λb向量的线性运算向量a沿着a的方向或a的反方向扩大或缩小4.共线向量定理
非零向量a与向量b共线,当且仅当存在唯一一个实数λ,使b=λa.重点:1.向量减法运算的应用.
2.向量的数乘运算及其几何意义.
难点:1.向量减法的几何意义.
2.向量数乘的几何意义及线性运算.1.应注意向量减法与加法的区别.作向量减法时,一是移到同一起点,二是转化为加法,要深刻领会其几何意义,千万不要弄错向量的方向.a-b与b-a的方向恰好相反.(4)注意a∥b与a=λb并不等价,若a=λb,则a与b一定共线,若a∥b,只有在b≠0时,才存在实数λ,使a=λb.
3.若a与b不共线,λa=μb,则λ=μ=0.[例1] 已知a,b,c,求作向量a-b+c(如图).[答案] 0
[例3] 计算:
①(-5)×4a;
②5(a+b)-4(a-b)-3a;
③(3a-5b+2c)-4(2a-b+3c).
[解析] ①原式=(-5×4)a=-20a.
②原式=5a+5b-4a+4b-3a=-2a+9b.
③原式=3a-5b+2c-8a+4b-12c=-5a-b-10c.[分析] 依据向量加法、减法的定义和数乘向量的几何意义,将待求向量逐步向已知条件过渡.[答案] B (2)∵ka+b与a+kb共线,
∴存在实数λ,使ka+b=λ(a+kb)
即ka+b=λa+λkb,∴(k-λ)a=(λk-1)b,
∵a、b是不共线的两个非零向量,
∴k-λ=λk-1=0,∴k2-1=0.∴k=±1.一、选择题
1.化简 [2(2a+8b)-4(4a-2b)]的结果为
( )
A.2a-b B.2b-a
C.a-b D.b-a
[答案] B[答案] A 3.设a、b是两个非零向量,e1、e2分别是a、b方向上的单位向量,则下列命题正确的是 ( )
A.若a∥b,则e1=e2
B.若a∥b,则|e1-e2|=2
C.若|a|=1,则a=e1
D.若|a|=|b|=1,则e1=e2或e1=-e2
[答案] C
[解析] 若a∥b,则a与b同向或反向,∴e1与e2同向或反向.∴选项A,B不对.
若|a|=|b|=1,可知a=e1,b=e2,但不一定有e1=e2或e1=-e2,∴选项D不对,故选C.[答案] D [答案] C [答案] 13 9.若向量a与b共线,且|a|=|b|=1,则|a-b|=______.
[答案] 0或2
[解析] 当a与b同向时,|a-b|=0,
当a与b反向时,|a-b|=2.
我们规定,与a长度 ,方向 的向量,叫做a的相反向量,记作-a,零向量的相反向量仍是 .
关于相反向量有以下结论
①-(-a)= ;
②a+(-a)=(-a)+a= ;
③若a、b是互为相反的向量,则b=-a,a+b= .相等相反零向量a002.向量减法
(1)定义
我们定义a-b=a+ ,即减去一个向量等于加上这个向量的 .
(2)向量减法的作图
因为(a-b)+b=a+[(-b)+b]=a+0=a,所以求a-b就是求这样一个向量,它与b的和等于a,从而得到a-b的作图法.相反向量(-b)3.向量数乘
一般地,我们规定实数λ与向量a的积是一个向量,这种运算叫做向量的数乘,记作λa.它的长度及方向规定如下:
(1)|λa|= ;
(2)λ>0时,λa的方向与a的方向 ;λ<0时,λa的方向与a的方向 ;
(3)当λ=0时,λa= .
注意向量数乘的结果仍是一个向量.
向量数乘满足下列运算律,设λ、μ为实数|λ|·|a|相同相反0(1)λ(μa)= .
(2)(λ+μ)a= .
(3)λ(a+b)= .
向量的加、减、数乘运算统称为 .
向量数乘的几何意义
向量数乘的几何意义就是把 .当λ>0时,沿着a的方向扩大(λ>1)或缩小(0<λ<1)λ倍;当λ<0时,沿着a的反方向扩大(|λ|>1)或缩小(|λ|<1)|λ|倍.λuaλa+μaλa+λb向量的线性运算向量a沿着a的方向或a的反方向扩大或缩小4.共线向量定理
非零向量a与向量b共线,当且仅当存在唯一一个实数λ,使b=λa.重点:1.向量减法运算的应用.
2.向量的数乘运算及其几何意义.
难点:1.向量减法的几何意义.
2.向量数乘的几何意义及线性运算.1.应注意向量减法与加法的区别.作向量减法时,一是移到同一起点,二是转化为加法,要深刻领会其几何意义,千万不要弄错向量的方向.a-b与b-a的方向恰好相反.(4)注意a∥b与a=λb并不等价,若a=λb,则a与b一定共线,若a∥b,只有在b≠0时,才存在实数λ,使a=λb.
3.若a与b不共线,λa=μb,则λ=μ=0.[例1] 已知a,b,c,求作向量a-b+c(如图).[答案] 0
[例3] 计算:
①(-5)×4a;
②5(a+b)-4(a-b)-3a;
③(3a-5b+2c)-4(2a-b+3c).
[解析] ①原式=(-5×4)a=-20a.
②原式=5a+5b-4a+4b-3a=-2a+9b.
③原式=3a-5b+2c-8a+4b-12c=-5a-b-10c.[分析] 依据向量加法、减法的定义和数乘向量的几何意义,将待求向量逐步向已知条件过渡.[答案] B (2)∵ka+b与a+kb共线,
∴存在实数λ,使ka+b=λ(a+kb)
即ka+b=λa+λkb,∴(k-λ)a=(λk-1)b,
∵a、b是不共线的两个非零向量,
∴k-λ=λk-1=0,∴k2-1=0.∴k=±1.一、选择题
1.化简 [2(2a+8b)-4(4a-2b)]的结果为
( )
A.2a-b B.2b-a
C.a-b D.b-a
[答案] B[答案] A 3.设a、b是两个非零向量,e1、e2分别是a、b方向上的单位向量,则下列命题正确的是 ( )
A.若a∥b,则e1=e2
B.若a∥b,则|e1-e2|=2
C.若|a|=1,则a=e1
D.若|a|=|b|=1,则e1=e2或e1=-e2
[答案] C
[解析] 若a∥b,则a与b同向或反向,∴e1与e2同向或反向.∴选项A,B不对.
若|a|=|b|=1,可知a=e1,b=e2,但不一定有e1=e2或e1=-e2,∴选项D不对,故选C.[答案] D [答案] C [答案] 13 9.若向量a与b共线,且|a|=|b|=1,则|a-b|=______.
[答案] 0或2
[解析] 当a与b同向时,|a-b|=0,
当a与b反向时,|a-b|=2.
