1.平面向量的正交分解
图片预览











文档简介
课件51张PPT。1.平面向量的正交分解
如果e1、e2是平面内两个不共线向量,则对平面内任一向量a,由平面向量基本定理知,存在唯一一对实数λ,μ,使a=λe1+μe2,特别地,当e1 e2时,由e1与e2构成的基底称为正交基底.
把一个向量分解为 的向量,叫做把向量正交分解.
当正交基底的基向量e1与e2都是 向量时,是一种重要的情形.它能与平面直角坐标系建立联系,为我们研究问题带来方便.⊥两个互相垂直单位2.平面向量的坐标表示
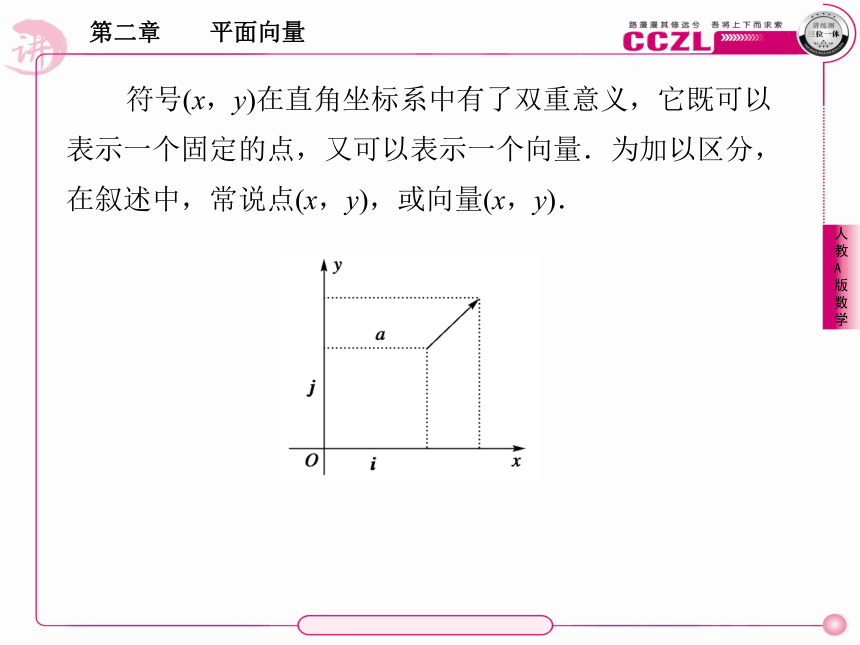
如图所示,在平面直角坐标系内,分别取与x轴、y轴方向相同的两个单位向量 作为基底,对于平面内任意一个向量a,由平面向量基本定理可知,有且只有一对实数x、y,使得a=xi+yj.这样,平面内的任一向量a都可由 唯一确定,我们把 叫做向量a的坐标,记作a=(x,y),x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.i,jx、y有序数对(x,y)符号(x,y)在直角坐标系中有了双重意义,它既可以表示一个固定的点,又可以表示一个向量.为加以区分,在叙述中,常说点(x,y),或向量(x,y).3.平面向量的坐标运算
(1)若a=(x1,y1),b=(x2,y2),
则a+b= ;
a-b= ;λa= .
(2)若A(x1,y1),B(x2,y2),则 = . (x1+x2,y1+y2)(x1-x2,y1-y2)(λx1,λy1)(x2-x1,y2-y1)4.完成下列各题
(1)已知m=(1,2),n=(-2,1),则3m-2n等于
( )
A.(7,4) B.(7,1)
C.(3,4) D.(3,-2)
(2)已知A(3,1),B(2,-1),则 的坐标是
( )
A.(-2,-1) B.(2,1)
C.(1,2) D.(-1,-2)(3)已知 =(3,4),A=(-2,-1),则B点的坐标为
( )
A.(5,5) B.(-5,-5)
C.(1,3) D.(-5,5)
(4)若a=(4,6),且a=2b,则b的坐标为
( )
A.(3,2) B.(2,3)
C.(-3,-2) D.(-2,-3)
[答案] (1)A (2)C (3)C (4)B重点:平面向量的正交分解,坐标运算.
难点:对平面向量的正交分解及坐标表示的理解和应用.1.点的坐标与向量的坐标是有区别的,平面向量的坐标与该向量的起点、终点坐标有关,只有起点在原点时,向量的坐标才与点的坐标相同.相等向量的坐标是相同的,但起点、终点的坐标却不一定相同.
2.用坐标表示的平面向量的线性运算,其推导可依据向量坐标的意义和向量线性运算的运算律进行.请自己写出推导过程.
3.向量的坐标运算为我们研究问题带来了方便,为我们用数形结合方法研究问题拓展了空间.要很好的体会总结,如何将几何问题向量化,并由向量运算的结果解释几何意义.[分析] 根据三角函数的定义,可求点A的坐标,即可得出 的坐标.[点评] 本题体现了三角函数在向量中的应用,随着学习的深入,不断总结相关知识的联系,形成有机的整体.
在上例中,其它条件不变,若∠xOA=150°,225°,300°,则向量 的坐标依次为________、________、________.[分析] 的坐标等于终点B的坐标减去起点A的坐标.[点评] 要搞清点的坐标,向量坐标的意义. [答案] (2,4),(-3,9),(-5,5)
已知点O(0,0)、A(1,2)、B(4,5),向量
(1)t为何值时,点P在x轴上?
(2)t为何值时,点P在第二象限?
(3)四边形ABPO能否为平行四边形?若能,求出t的值;若不能,说明理由.[例5] 已知平行四边形的三个顶点坐标为A(0,0),B(0,b),C(a,c).求第四个顶点D的坐标.[辨析] 平行四边形四个顶点按逆时针顺序排列有三种可能,即ACDB、ACBD、ADCB.而错解只考虑了ACDB一种情形,而疏漏了另两种情况.[点评] 注意本例与教材97页例5的区别,你能找出这两例有何不同吗?[答案] A 2.已知a=(-1,2),b=(-1,1),c=(3,-2),用a、b作基底,可将向量c表示为c=pa+qb,则
( )
A.p=4,q=1 B.p=1,q=-4
C.p=0,q=4 D.p=1,q=4
[答案] B
[解析] ∵c=pa+qb=(-p-q,2p+q),[答案] C [答案] (-18,18),(-3,-3) 6.以a=(1,1),b=(-2,3)为一组基底,表示c=(2,1),则c=________.
如果e1、e2是平面内两个不共线向量,则对平面内任一向量a,由平面向量基本定理知,存在唯一一对实数λ,μ,使a=λe1+μe2,特别地,当e1 e2时,由e1与e2构成的基底称为正交基底.
把一个向量分解为 的向量,叫做把向量正交分解.
当正交基底的基向量e1与e2都是 向量时,是一种重要的情形.它能与平面直角坐标系建立联系,为我们研究问题带来方便.⊥两个互相垂直单位2.平面向量的坐标表示
如图所示,在平面直角坐标系内,分别取与x轴、y轴方向相同的两个单位向量 作为基底,对于平面内任意一个向量a,由平面向量基本定理可知,有且只有一对实数x、y,使得a=xi+yj.这样,平面内的任一向量a都可由 唯一确定,我们把 叫做向量a的坐标,记作a=(x,y),x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.i,jx、y有序数对(x,y)符号(x,y)在直角坐标系中有了双重意义,它既可以表示一个固定的点,又可以表示一个向量.为加以区分,在叙述中,常说点(x,y),或向量(x,y).3.平面向量的坐标运算
(1)若a=(x1,y1),b=(x2,y2),
则a+b= ;
a-b= ;λa= .
(2)若A(x1,y1),B(x2,y2),则 = . (x1+x2,y1+y2)(x1-x2,y1-y2)(λx1,λy1)(x2-x1,y2-y1)4.完成下列各题
(1)已知m=(1,2),n=(-2,1),则3m-2n等于
( )
A.(7,4) B.(7,1)
C.(3,4) D.(3,-2)
(2)已知A(3,1),B(2,-1),则 的坐标是
( )
A.(-2,-1) B.(2,1)
C.(1,2) D.(-1,-2)(3)已知 =(3,4),A=(-2,-1),则B点的坐标为
( )
A.(5,5) B.(-5,-5)
C.(1,3) D.(-5,5)
(4)若a=(4,6),且a=2b,则b的坐标为
( )
A.(3,2) B.(2,3)
C.(-3,-2) D.(-2,-3)
[答案] (1)A (2)C (3)C (4)B重点:平面向量的正交分解,坐标运算.
难点:对平面向量的正交分解及坐标表示的理解和应用.1.点的坐标与向量的坐标是有区别的,平面向量的坐标与该向量的起点、终点坐标有关,只有起点在原点时,向量的坐标才与点的坐标相同.相等向量的坐标是相同的,但起点、终点的坐标却不一定相同.
2.用坐标表示的平面向量的线性运算,其推导可依据向量坐标的意义和向量线性运算的运算律进行.请自己写出推导过程.
3.向量的坐标运算为我们研究问题带来了方便,为我们用数形结合方法研究问题拓展了空间.要很好的体会总结,如何将几何问题向量化,并由向量运算的结果解释几何意义.[分析] 根据三角函数的定义,可求点A的坐标,即可得出 的坐标.[点评] 本题体现了三角函数在向量中的应用,随着学习的深入,不断总结相关知识的联系,形成有机的整体.
在上例中,其它条件不变,若∠xOA=150°,225°,300°,则向量 的坐标依次为________、________、________.[分析] 的坐标等于终点B的坐标减去起点A的坐标.[点评] 要搞清点的坐标,向量坐标的意义. [答案] (2,4),(-3,9),(-5,5)
已知点O(0,0)、A(1,2)、B(4,5),向量
(1)t为何值时,点P在x轴上?
(2)t为何值时,点P在第二象限?
(3)四边形ABPO能否为平行四边形?若能,求出t的值;若不能,说明理由.[例5] 已知平行四边形的三个顶点坐标为A(0,0),B(0,b),C(a,c).求第四个顶点D的坐标.[辨析] 平行四边形四个顶点按逆时针顺序排列有三种可能,即ACDB、ACBD、ADCB.而错解只考虑了ACDB一种情形,而疏漏了另两种情况.[点评] 注意本例与教材97页例5的区别,你能找出这两例有何不同吗?[答案] A 2.已知a=(-1,2),b=(-1,1),c=(3,-2),用a、b作基底,可将向量c表示为c=pa+qb,则
( )
A.p=4,q=1 B.p=1,q=-4
C.p=0,q=4 D.p=1,q=4
[答案] B
[解析] ∵c=pa+qb=(-p-q,2p+q),[答案] C [答案] (-18,18),(-3,-3) 6.以a=(1,1),b=(-2,3)为一组基底,表示c=(2,1),则c=________.
