2.5 平面向量应用举例
图片预览









文档简介
课件66张PPT。2.5 平面向量应用举例 1.平面几何中的许多问题:如线段长度(距离)、夹角、平行、垂直、点共线等都可以通过向量的 及 表示出来.线性运算数量积2.用向量方法解决平面几何问题的“三步曲”
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系;
(3)把运算结果“翻译”成几何关系.3.向量的物理背景
(1)向量是既有大小又有方向的量,物理中有许多量,比如力、速度、加速度、位移等都是向量.
(2)物理学中相关知识与向量的联系
①力、速度、加速度、位移的合成与分解就是向量的加减法,运动的叠加亦用到向量的合成;
②动量mv是数乘向量;
③功W是力F与所产生位移s的数量积.重点:用向量方法解决实际问题的基本方法;用向量法解决几何问题的“三步曲”.
难点:实际问题转化为向量问题.1.力向量
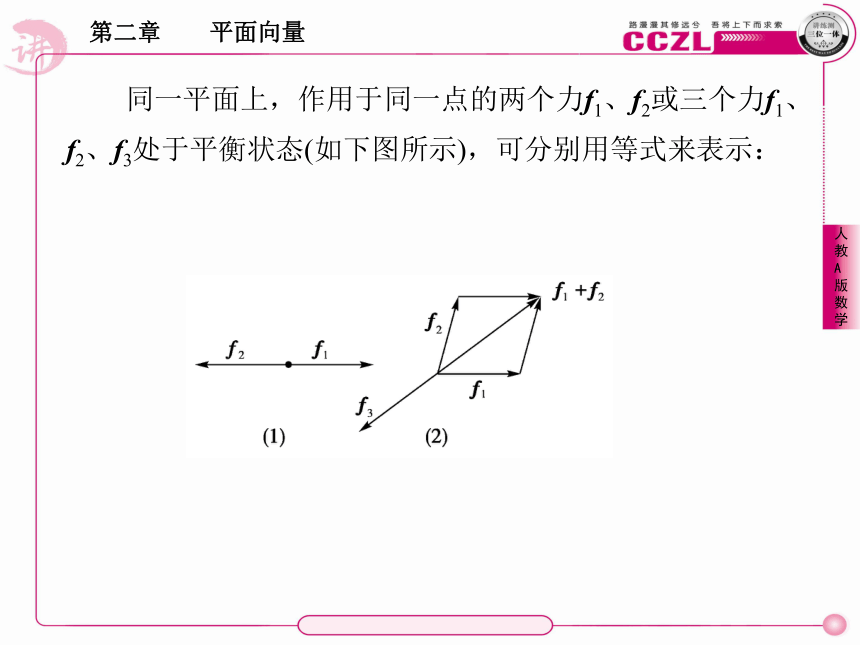
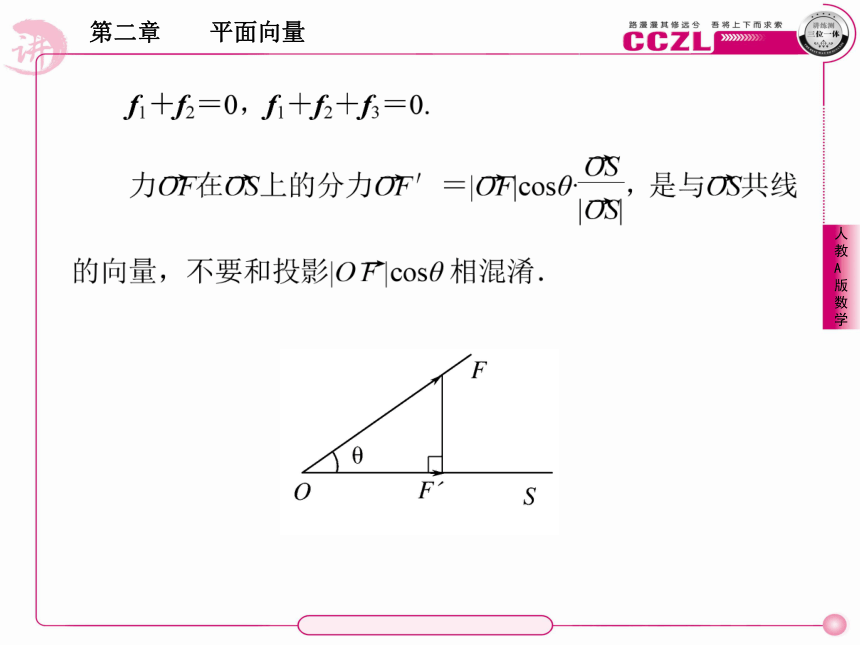
力向量与前面学过的自由向量有些不同,它不仅包括大小、方向两个要素,而且还有作用点.大小和方向相同的两个力,如果作用点不同,那么它们是不相等的.但力是具有大小和方向的量,在不计作用点的情况下,可利用向量法则进行计算.例如,求作用于同一点的两个力的合力,可用向量求和的平行四边形法则(如图所示).同一平面上,作用于同一点的两个力f1、f2或三个力f1、f2、f3处于平衡状态(如下图所示),可分别用等式来表示:2.速度向量
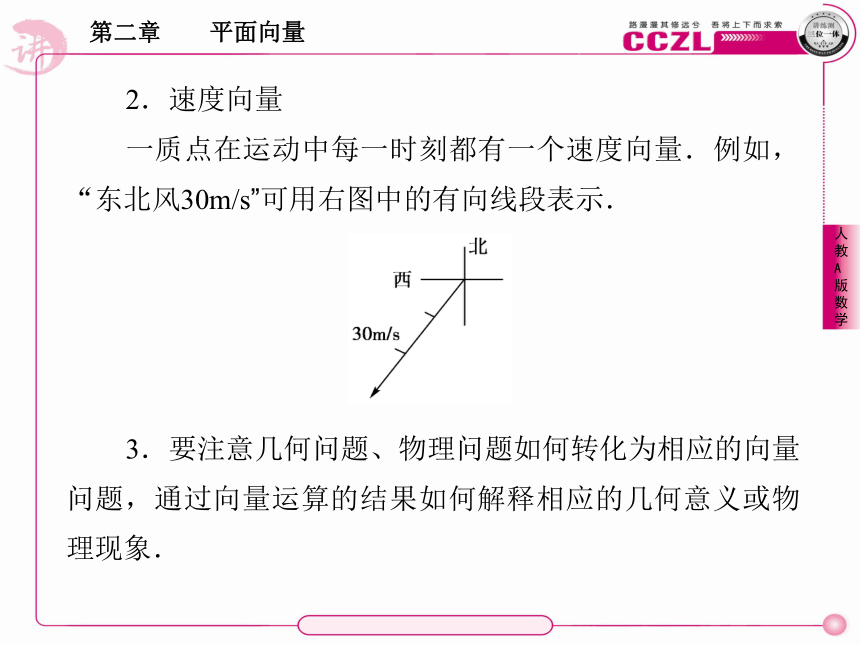
一质点在运动中每一时刻都有一个速度向量.例如,“东北风30m/s”可用右图中的有向线段表示.
3.要注意几何问题、物理问题如何转化为相应的向量问题,通过向量运算的结果如何解释相应的几何意义或物理现象.
[例1] 已知△ABC中,a=2,b=3,C=60°,试用向量法求c.
[分析] 一般地求两点间距离(线段长度)的问题,可转化为求向量的模,利用|a|2=a·a解决.
如图所示,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2.则对角线AC的长为________.
[例2] 已知:AD、BE、CF是△ABC的三条高,O为三条高线的交点,DG⊥BE于G,DH⊥CF于H,如图所示.
求证:HG∥EF.
平行四边形ABCD中,E、F分别为AB、CD上的点,AE=CF,P、Q分别为AD、BC上的点,AP=CQ,求证四边形PEQF为平行四边形.
[例3] 如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2.
求证:AD⊥BC.
[例4] 如图所示,在细绳l上作用着一个400N的力,与水平方向的夹角为60°,细绳上挂着一个重物,使细绳的另一段处于水平状态,求物体所受重力G是多少?
[例5] 已知两恒力F1=(3,4)、F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),试求:(1)F1,F2分别对质点所做的功;(2)F1,F2的合力F对质点所做的功.(力的单位:N 位移单位:m)
[分析] 设物体在力F作用下的位移为s,则所做的功为W=F·s.[点评] 物理上力做功的实质是力在物体前进方向上的分力与物体位移距离的乘积,它的实质是向量的数量积.
两个力F1=i+j,F2=4i-5j,作用于同一质点,使该质点从A(20,15)移动到B(7,0),其中i,j是x轴、y轴正方向上的单位向量.则:
(1)F1,F2对该质点做的功分别为______,________.
(2)F1,F2的合力F对该质点做的功为________.
(力的单位:N 位移单位:m)
[答案] (1)-28J 23J (2)-5J
[例6] 已知一只蚂蚁在地面上的一个三角形区域ABC内爬行,试问当蚂蚁爬到这个三角形区域的什么位置时,它到这个三角形的三个顶点间的距离的平方和最小?
求证:(ac+bd)2≤(a2+b2)(c2+d2).[点评] 待解决的代数、几何、三角、物理等问题,只要其表达式能用向量运算来表示,就可以考虑使用向量方法去试着解决.
本例中a2+b2,c2+d2与向量的模有联系,而ac+bd与向量的数量积有联系,故可尝试能否设出向量来表示.[例7] 质量为2kg的木块,在平行于斜面向上的拉力F=10N的作用下,沿倾斜角θ=30°的光滑斜面向上滑行2m的距离(如图)
(1)分别求物体所受各力在这一过程中对物体做的功;
(2)在这一过程中,物体所受各力对物体做的功的代数和是多少?
(3)求物体所受合外力对物体所做的功,并指出它与物体所受各个力对物体做功的代数和之间有什么关系.
(取g=9.8m/s2)[解析] (1)木块受三个力的作用,重力G,拉力F和支持力FN,如图所示.拉力F与位移s方向相同,所以拉力对木块所做的功为:
WF=F·s=|F||s|cos0°=20(J).
支持力FN与位移方向垂直,不做功,所以
WN=FN·s=0.
重力G对物体所做的功为:
WG=G·s=|G||s|cos(90°+θ)(2)物体所受各力对物体做功的代数和为:
W=WF+WN+WG=0.4(J).
(3)物体所受合外力的大小为:
|F合|=|F|-|G|sin30°=0.2(N).
所以,合外力对物体所做的功为:W=F合·s=0.4(J).
所以,物体所受合外力对物体所做的功,与物体所受各力对物体做功的代数和相等.一、选择题
1.已知A(2,1),B(3,2),C(-1,4),则△ABC是
( )
A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
[答案] C2.如图所示,一力作用在小车上,其中力F的大小为10N,方向与水平面成60°,当小车向前运动10米,则力F做的功为
( )
A.100焦耳 B.50焦耳
C.50 焦耳 D.200焦耳
[答案] B
[解析] 依题意有W=F·s=|F||s|·cos60°=10×10×
=50J,故选B.[答案] B 二、填空题
4.(08·上海理)若向量a、b满足|a|=1,|b|=2,且a与b的夹角为 ,则|a+b|=________.[答案] 等腰 [答案] 3 7.用两条成120°角的等长绳子悬挂一个灯具,已知灯具重量为10N,则每根绳子的拉力大小为________.
[答案] 10N8.三个力F1、F2、F3同时作用于O点且处于平衡状态,已知F1与F3的夹角为120°,又|F1|=|F2|=20N,则|F3|=________.
[答案] 20N
[解析] ∵F1+F2+F3=0,∴F3=-(F1+F2),
∴|F3|2=(F1+F2)2=(20)2+(20)2+2·20·20cos120°=400,∴|F3|=20.三、解答题
9.如图所示,在平行四边形ABCD的对角线DB的延长线及反向延长线上分别取E、F两点,使BE=DF,求证:四边形AECF也是平行四边形.11.如图所示,已知D、E为△ABC的边AB、AC的中点,延长CD到M使DM=CD,延长BE至N使EN=BE,求证:M、A、N三点共线.
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系;
(3)把运算结果“翻译”成几何关系.3.向量的物理背景
(1)向量是既有大小又有方向的量,物理中有许多量,比如力、速度、加速度、位移等都是向量.
(2)物理学中相关知识与向量的联系
①力、速度、加速度、位移的合成与分解就是向量的加减法,运动的叠加亦用到向量的合成;
②动量mv是数乘向量;
③功W是力F与所产生位移s的数量积.重点:用向量方法解决实际问题的基本方法;用向量法解决几何问题的“三步曲”.
难点:实际问题转化为向量问题.1.力向量
力向量与前面学过的自由向量有些不同,它不仅包括大小、方向两个要素,而且还有作用点.大小和方向相同的两个力,如果作用点不同,那么它们是不相等的.但力是具有大小和方向的量,在不计作用点的情况下,可利用向量法则进行计算.例如,求作用于同一点的两个力的合力,可用向量求和的平行四边形法则(如图所示).同一平面上,作用于同一点的两个力f1、f2或三个力f1、f2、f3处于平衡状态(如下图所示),可分别用等式来表示:2.速度向量
一质点在运动中每一时刻都有一个速度向量.例如,“东北风30m/s”可用右图中的有向线段表示.
3.要注意几何问题、物理问题如何转化为相应的向量问题,通过向量运算的结果如何解释相应的几何意义或物理现象.
[例1] 已知△ABC中,a=2,b=3,C=60°,试用向量法求c.
[分析] 一般地求两点间距离(线段长度)的问题,可转化为求向量的模,利用|a|2=a·a解决.
如图所示,平行四边形ABCD中,已知AD=1,AB=2,对角线BD=2.则对角线AC的长为________.
[例2] 已知:AD、BE、CF是△ABC的三条高,O为三条高线的交点,DG⊥BE于G,DH⊥CF于H,如图所示.
求证:HG∥EF.
平行四边形ABCD中,E、F分别为AB、CD上的点,AE=CF,P、Q分别为AD、BC上的点,AP=CQ,求证四边形PEQF为平行四边形.
[例3] 如图所示,若D是△ABC内的一点,且AB2-AC2=DB2-DC2.
求证:AD⊥BC.
[例4] 如图所示,在细绳l上作用着一个400N的力,与水平方向的夹角为60°,细绳上挂着一个重物,使细绳的另一段处于水平状态,求物体所受重力G是多少?
[例5] 已知两恒力F1=(3,4)、F2=(6,-5)作用于同一质点,使之由点A(20,15)移动到点B(7,0),试求:(1)F1,F2分别对质点所做的功;(2)F1,F2的合力F对质点所做的功.(力的单位:N 位移单位:m)
[分析] 设物体在力F作用下的位移为s,则所做的功为W=F·s.[点评] 物理上力做功的实质是力在物体前进方向上的分力与物体位移距离的乘积,它的实质是向量的数量积.
两个力F1=i+j,F2=4i-5j,作用于同一质点,使该质点从A(20,15)移动到B(7,0),其中i,j是x轴、y轴正方向上的单位向量.则:
(1)F1,F2对该质点做的功分别为______,________.
(2)F1,F2的合力F对该质点做的功为________.
(力的单位:N 位移单位:m)
[答案] (1)-28J 23J (2)-5J
[例6] 已知一只蚂蚁在地面上的一个三角形区域ABC内爬行,试问当蚂蚁爬到这个三角形区域的什么位置时,它到这个三角形的三个顶点间的距离的平方和最小?
求证:(ac+bd)2≤(a2+b2)(c2+d2).[点评] 待解决的代数、几何、三角、物理等问题,只要其表达式能用向量运算来表示,就可以考虑使用向量方法去试着解决.
本例中a2+b2,c2+d2与向量的模有联系,而ac+bd与向量的数量积有联系,故可尝试能否设出向量来表示.[例7] 质量为2kg的木块,在平行于斜面向上的拉力F=10N的作用下,沿倾斜角θ=30°的光滑斜面向上滑行2m的距离(如图)
(1)分别求物体所受各力在这一过程中对物体做的功;
(2)在这一过程中,物体所受各力对物体做的功的代数和是多少?
(3)求物体所受合外力对物体所做的功,并指出它与物体所受各个力对物体做功的代数和之间有什么关系.
(取g=9.8m/s2)[解析] (1)木块受三个力的作用,重力G,拉力F和支持力FN,如图所示.拉力F与位移s方向相同,所以拉力对木块所做的功为:
WF=F·s=|F||s|cos0°=20(J).
支持力FN与位移方向垂直,不做功,所以
WN=FN·s=0.
重力G对物体所做的功为:
WG=G·s=|G||s|cos(90°+θ)(2)物体所受各力对物体做功的代数和为:
W=WF+WN+WG=0.4(J).
(3)物体所受合外力的大小为:
|F合|=|F|-|G|sin30°=0.2(N).
所以,合外力对物体所做的功为:W=F合·s=0.4(J).
所以,物体所受合外力对物体所做的功,与物体所受各力对物体做功的代数和相等.一、选择题
1.已知A(2,1),B(3,2),C(-1,4),则△ABC是
( )
A.等边三角形 B.钝角三角形
C.直角三角形 D.锐角三角形
[答案] C2.如图所示,一力作用在小车上,其中力F的大小为10N,方向与水平面成60°,当小车向前运动10米,则力F做的功为
( )
A.100焦耳 B.50焦耳
C.50 焦耳 D.200焦耳
[答案] B
[解析] 依题意有W=F·s=|F||s|·cos60°=10×10×
=50J,故选B.[答案] B 二、填空题
4.(08·上海理)若向量a、b满足|a|=1,|b|=2,且a与b的夹角为 ,则|a+b|=________.[答案] 等腰 [答案] 3 7.用两条成120°角的等长绳子悬挂一个灯具,已知灯具重量为10N,则每根绳子的拉力大小为________.
[答案] 10N8.三个力F1、F2、F3同时作用于O点且处于平衡状态,已知F1与F3的夹角为120°,又|F1|=|F2|=20N,则|F3|=________.
[答案] 20N
[解析] ∵F1+F2+F3=0,∴F3=-(F1+F2),
∴|F3|2=(F1+F2)2=(20)2+(20)2+2·20·20cos120°=400,∴|F3|=20.三、解答题
9.如图所示,在平行四边形ABCD的对角线DB的延长线及反向延长线上分别取E、F两点,使BE=DF,求证:四边形AECF也是平行四边形.11.如图所示,已知D、E为△ABC的边AB、AC的中点,延长CD到M使DM=CD,延长BE至N使EN=BE,求证:M、A、N三点共线.
