数系的扩充和复数的概念

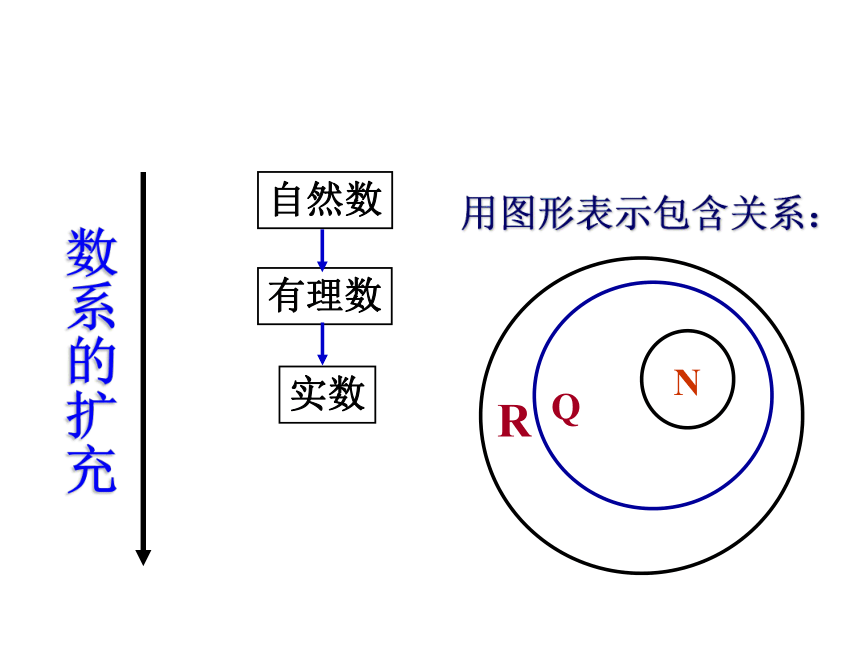
课件18张PPT。3.1.1 数系的扩充与复数的概念2019年3月9日阅读教材81—82页 回答下列问题1 数系（数集）扩充的轨迹是什么？2 数系扩充的原动力是什么？数系的扩充自然数用图形表示包含关系：引入一个新数： 现在我们就引入这样一个数 i ，把 i 叫做虚数单位，并且规定：

（2）实数可以与 i 进行四则运算，在进行四则运算时，原有的加法与乘法的运算率(包括交换率、结合率和分配率)仍然成立。 解下列方程
(1)x2+15=0；
(2)x2-x+1=0； (3)ax2+bx+c=0； 设a,b都是实数
形如a+bi(a,b∈R)的数叫做复数. 全体复数所形成的集合叫做复数集，
一般用字母C表示 .复数定义复数的代数形式：复数通常用字母 z表示，即其中 称为虚数单位。复数a+bi复数集虚数集实数集纯虚数集复数集、实数集、虚数集、纯虚数集之间的关系两个复数可否比较大小？思考练一练：1.说明下列数中，那些是实数，哪些是虚数，哪些是纯虚数，并指出复数的实部与虚部。5 +8，0 如果两个复数的实部和虚部分别相等，那么我们就说这两个复数相等．复数相等例1: 实数x取什么值时，复数

（1）是实数？（2）是虚数？（3）是纯虚数？解: （1）当 ，即 时，复数z 是实数．（2）当 ，即 时，复数z 是虚数．（3）当即 时，复数z 是
纯虚数．练习:当m为何实数时，复数
（1）实数 （2）虚数 （3）纯虚数(3)m=-2(1)m=(2)m解：根据复数相等的定义，得方程组巩固提高
完成学案课时检测小结:1.虚数单位i的引入；