3.2.1复数的加法和减法
图片预览


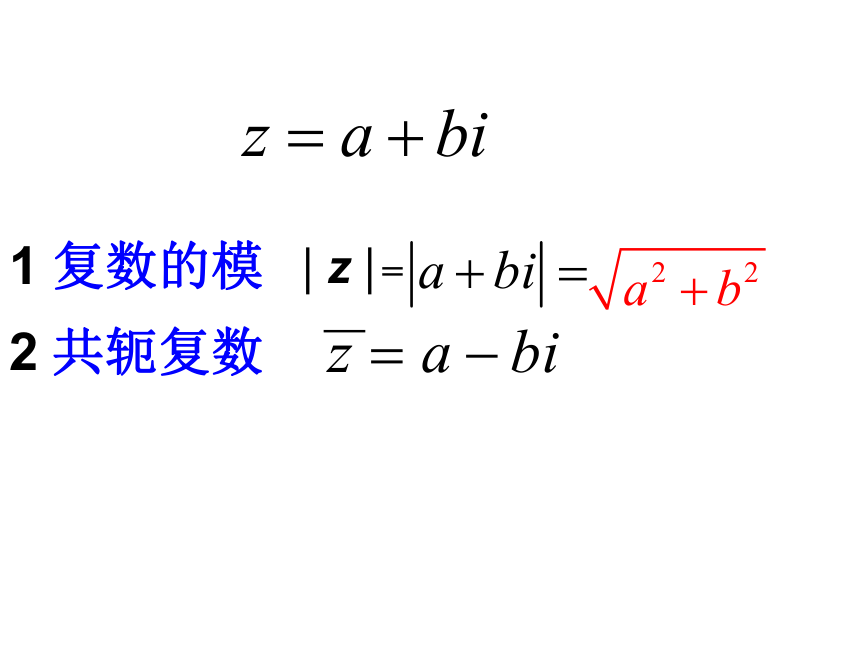



文档简介
课件13张PPT。3.2 复数的运算2019年3月9日3.2.1复数的加法和减法复数z=a+bi直角坐标系中的点Z(a,b)一一对应平面向量一一对应一一对应复数的几何意义?xyobaZ(a,b)z=a+bi复习2 共轭复数=| z | 1 复数的模设z1=a+bi,z2=c+di (a、b、c、d∈R) 那么它们的和:(a+bi)+(c+di)=(a+c)+(b+d)i点评:(1)复数的加法运算法则是一种规定。(2)很明显,两个复数的和仍 然是一个复数。1、复数的加法法则: 两个复数相加就是把实部与实部、虚部与虚部分别相加。证:设Z1=a1+b1i,Z2=a2+b2i,Z3=a3+b3i 则Z1+Z2=(a1+a2)+(b1+b2)i,Z2+Z1=(a2+a1)+(b2+b1)i显然 Z1+Z2=Z2+Z1同理可得 (Z1+Z2)+Z3=Z1+(Z2+Z3)点评:实数加法运算的交换律、结合律在复数集C中依然成立。运算律探究?复数的加法满足交换律,结合律吗?思考?复数是否有减法? 两个复数相减就是把实部与实部、虚部与虚部分别相减。设z1=a+bi,z2=c+di (a、b、c、d∈R)
那么它们的差:复数的减法 两个复数相减就是把实部与实部、虚部与虚部分别相减。设z1=a+bi,z2=c+di (a、b、c、d∈R)
那么它们的差:基础题型一
例题1例题2xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)1.复数加法运算的几何意义?问题探索结论:复数的加法可以按照向量的加法来进行 复数的和对应向量的和。 xoyZ1(a,b)Z2(c,d)2.复数减法运算的几何意义?问题探索结论:复数的减法可以按照向量的减法来进行 复数的和对应向量的和。 xoyZ1(a,b)Z2(c,d)复数z1-z2向量Z2Z12.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离转化推广(1)|z-(1+2i)|(2)|z+(1+2i)|已知复数z对应点A,说明下列各式所表示的几何意义.点Z到点(1,2)的距离点Z到点(-1, -2)的距离(3)|z+2i|点Z到点(0, -2)的距离复数减法的几何意义的运用 设复数z=x+yi,(x,y∈R),在下列条件下求动点Z(x,y)的轨迹.
|z-2|= 1
2. |z-i|+ |z+i|=4
3. |z-2|= |z+4|
那么它们的差:复数的减法 两个复数相减就是把实部与实部、虚部与虚部分别相减。设z1=a+bi,z2=c+di (a、b、c、d∈R)
那么它们的差:基础题型一
例题1例题2xoyZ1(a,b)Z2(c,d)Z(a+c,b+d)1.复数加法运算的几何意义?问题探索结论:复数的加法可以按照向量的加法来进行 复数的和对应向量的和。 xoyZ1(a,b)Z2(c,d)2.复数减法运算的几何意义?问题探索结论:复数的减法可以按照向量的减法来进行 复数的和对应向量的和。 xoyZ1(a,b)Z2(c,d)复数z1-z2向量Z2Z12.复数减法运算的几何意义?|z1-z2|表示什么?表示复平面上两点Z1 ,Z2的距离转化推广(1)|z-(1+2i)|(2)|z+(1+2i)|已知复数z对应点A,说明下列各式所表示的几何意义.点Z到点(1,2)的距离点Z到点(-1, -2)的距离(3)|z+2i|点Z到点(0, -2)的距离复数减法的几何意义的运用 设复数z=x+yi,(x,y∈R),在下列条件下求动点Z(x,y)的轨迹.
|z-2|= 1
2. |z-i|+ |z+i|=4
3. |z-2|= |z+4|
