弧、弦圆心角

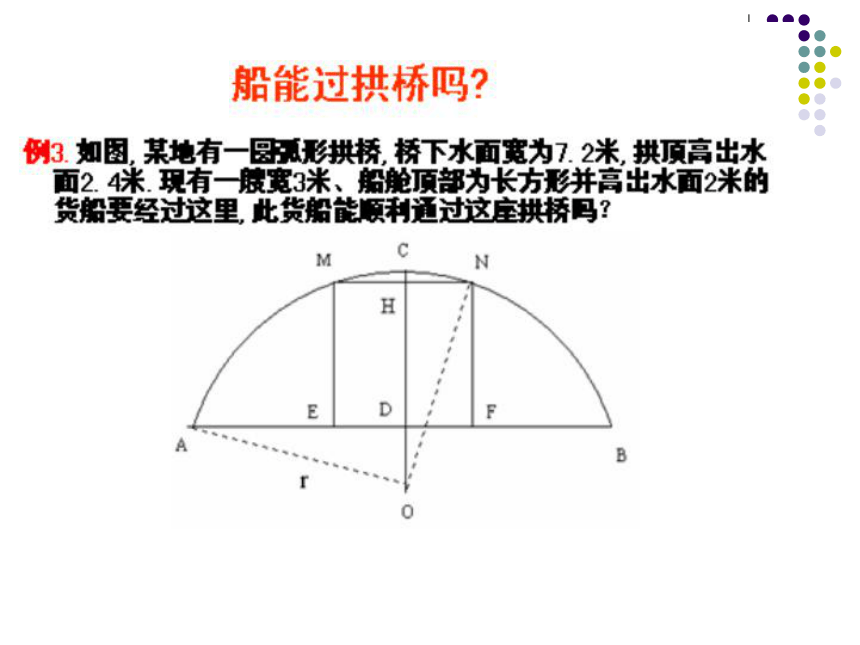
课件21张PPT。24.1.3 弧、弦、圆心角船能过拱桥吗解:如图,用 表示桥拱, 所在圆的圆心为O,半径为Rm,
经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C.根
据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.
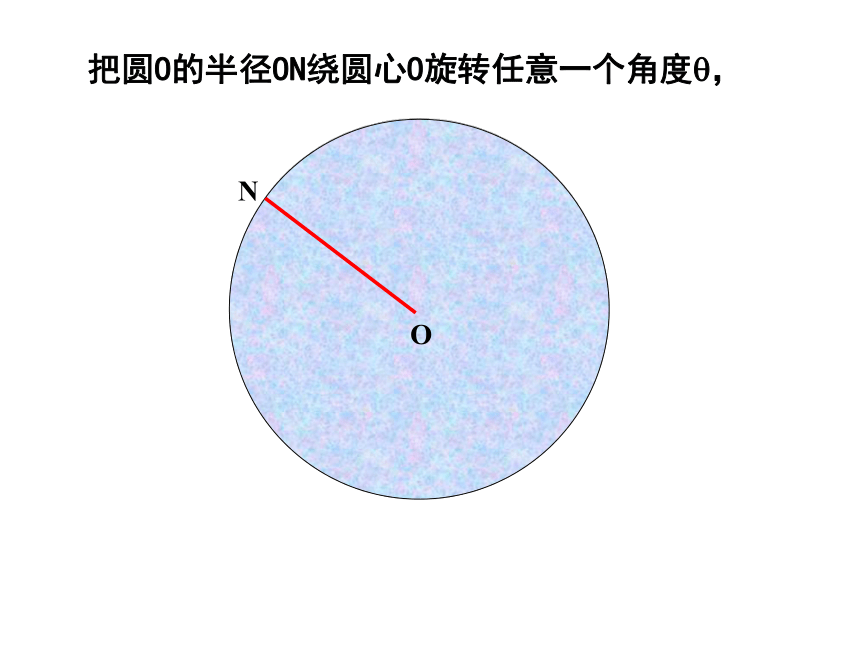
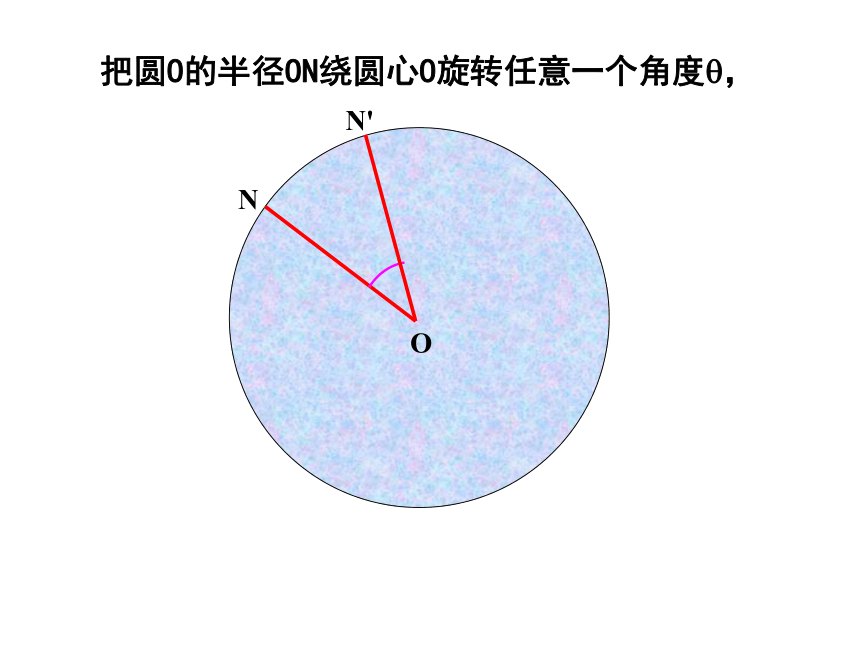
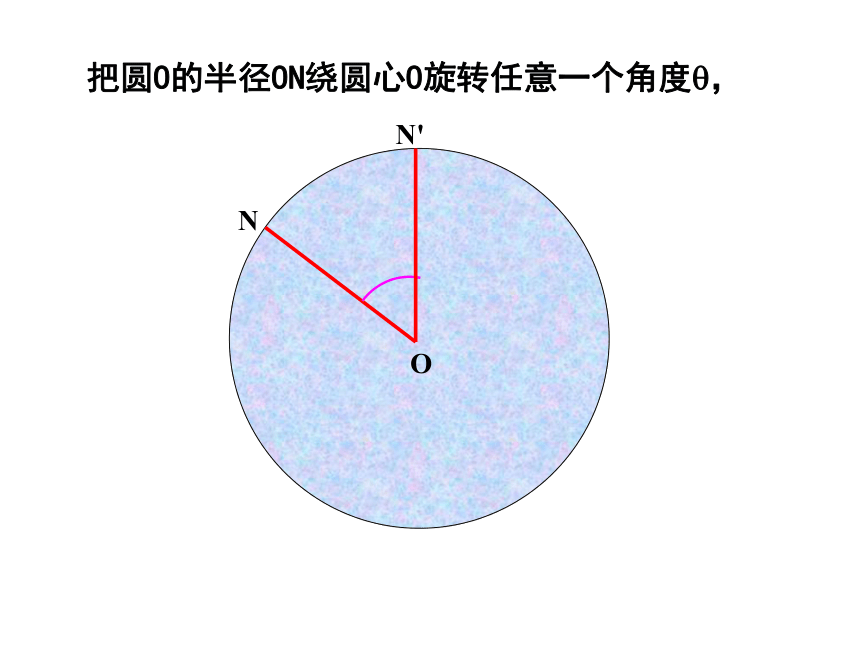
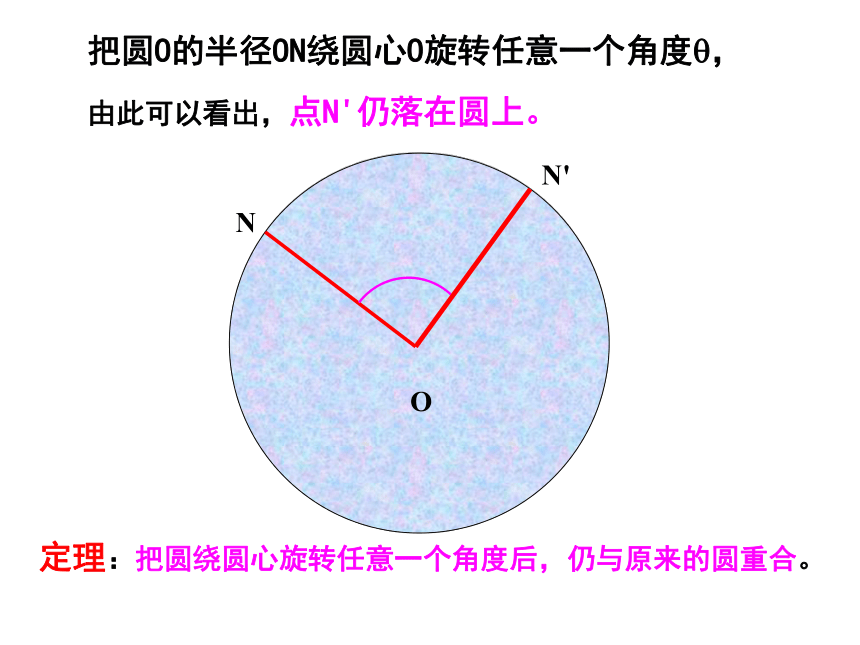
由题设得在Rt△OAD中，由勾股定理，得解得 R≈3.9（m）.在Rt△ONH中，由勾股定理，得∴此货船能顺利通过这座拱桥.圆是中心对称图形吗?它的对称中心在哪里?·一、思考圆是中心对称图形，它的对称中心是圆心.NO把圆O的半径ON绕圆心O旋转任意一个角度?，NON'?把圆O的半径ON绕圆心O旋转任意一个角度?，NON'?把圆O的半径ON绕圆心O旋转任意一个角度?，NON'?把圆O的半径ON绕圆心O旋转任意一个角度?，NON'?定理：把圆绕圆心旋转任意一个角度后，仍与原来的圆重合。把圆O的半径ON绕圆心O旋转任意一个角度?，由此可以看出，点N'仍落在圆上。· 圆心角：我们把顶点在圆心的角叫做圆心角.O二、概念如图中所示， ∠AOB就是一个圆心角。 如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时，显然∠AOB＝∠A′OB′，射线OA与OA′重合，OB与OB′重合．而同圆的半径相等，OA=OA′，OB=OB′，从而点A与A′重合，B与B′重合．·OAB·OABA′B′A′B′三、探究因此，弧AB与弧A1B1 重合，AB与A′B′重合．同样，还可以得到：
在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角_____， 所对的弦________；
在同圆或等圆中，如果两条弦相等，那么他们所对的圆心角______，所对的弧_________．这样，我们就得到下面的定理：相等相等相等相等四、定理证明：∵AB=AC∴ AB=AC, △ABC 等腰三角形．又∠ACB=60°，∴ △ABC是等边三角形，AB=BC=CA.∴ ∠AOB＝∠BOC＝∠AOC.·ABCO五、例题例1 如图在⊙O中，AB=AC ，∠ACB=60°，
求证:∠AOB=∠BOC=∠AOC.⌒⌒⌒⌒1.如图，AB、CD是⊙O的两条弦．
（1）如果AB=CD，那么___________，_________________．
（2）如果 = ，那么____________，______________．
（3）如果∠AOB=∠COD，那么_____________，____________．
（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？AB=CDAB=CD相 等 因为AB=CD ，所以∠AOB=∠COD. 又因为AO=CO，BO=DO， 所以△AOB ≌ △COD. 又因为OE 、OF是AB与CD对应边上的高，所以 OE = OF.六、练习2.如图，AB是⊙O的直径， , ∠COD=35°，
求∠AOE的度数．解：∵把圆心角等分成360份,则每一份的圆心角是1o.同时整个圆也被分成了360份.则每一份这样的弧叫做1o的弧.这样,1o的圆心角对着1o的弧,
1o的弧对着1o的圆心角.
n o的圆心角对着no的弧,
n o的弧对着no的圆心角.性质:弧的度数和它所对圆心角的度数相等.小结（2） 所对的圆心角和 所对的圆 心角相等在两个圆中，分别有 , 若 的度数和 相等，则有 （1） 和 相等判断结束试一试例2：如图，在⊙O中，弦AB所对的劣弧为圆的
，圆的半径为4cm，求AB的长C点此继续知识延伸弧的度数圆心角定理的应用圆心角定理圆心角的定义
学生练习圆的旋转不变性小结