二项式定理邢台州高中数学优质课课件
文档属性
| 名称 | 二项式定理邢台州高中数学优质课课件 |  | |
| 格式 | rar | ||
| 文件大小 | 359.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-08 13:52:00 | ||
图片预览






文档简介
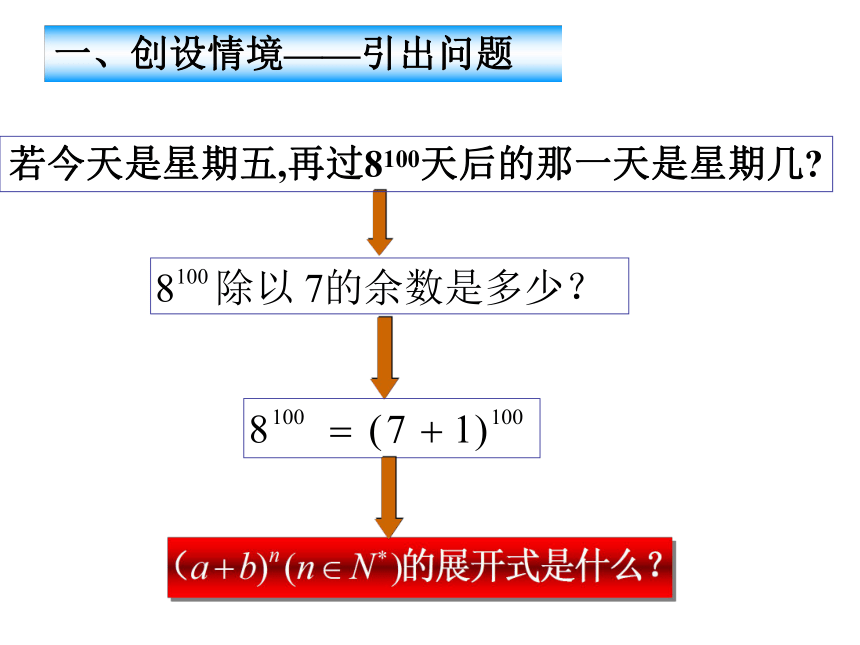
课件14张PPT。路桥中学 吴丽霞1.3.1二项式定理一、创设情境——引出问题 若今天是星期五,再过8100天后的那一天是星期几?①推陈出新= ?= ?……二、存疑设问——突破难点对 展开式的分析(a+b)2是2个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后, 才能得
到展开式的一项。由分步乘法计数原理, 在合并同类
项之前,(a+b)2的展开式共有22项,a2-kbk(k=0,1,2)对 展开式的分析(a+b)2是2个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有22项,而且每一项都是 的形式.
a2-kbk(k=0,1,2)思考:你能仿照上述过程,自己推导出 ,
的展开式吗?猜想:②初步归纳(a+b)n是n个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后, 才能得
到展开式的一项。由分步乘法计数原理, 在合并同类
项之前,(a+b)n的展开式共有2n项,an-kbk(k=0,1,2,…,n)证明:对于某个k (k∈{ }),0,1,2,…,n对应的项an-kbk是由n-k个(a+b)中选a,k个(a+b)中选b得到的.由于b选定后,a的选法也随之确定,因此, an-kbk出现的次数相当于从n个(a+b)中取k个b的组合数 ,这样,(a+b)n的展开式中,将它们合并同类项,就得到二项展开式:1.展开式共有n+1个项二项式定理(binomial theorem)公式特征:2.各项的次数都等于二项式的次数n;3.字母a的次数由n递减到0,字母b的次数由0递增到n.
特别地:若今天是星期五,再过8100天后的那一天是星期几?例题1:练习:必做题:P36 1,2,3作业 布置:小结:知识方面:方法方面:选做题:推导 的展开式。
到展开式的一项。由分步乘法计数原理, 在合并同类
项之前,(a+b)2的展开式共有22项,a2-kbk(k=0,1,2)对 展开式的分析(a+b)2是2个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有22项,而且每一项都是 的形式.
a2-kbk(k=0,1,2)思考:你能仿照上述过程,自己推导出 ,
的展开式吗?猜想:②初步归纳(a+b)n是n个(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后, 才能得
到展开式的一项。由分步乘法计数原理, 在合并同类
项之前,(a+b)n的展开式共有2n项,an-kbk(k=0,1,2,…,n)证明:对于某个k (k∈{ }),0,1,2,…,n对应的项an-kbk是由n-k个(a+b)中选a,k个(a+b)中选b得到的.由于b选定后,a的选法也随之确定,因此, an-kbk出现的次数相当于从n个(a+b)中取k个b的组合数 ,这样,(a+b)n的展开式中,将它们合并同类项,就得到二项展开式:1.展开式共有n+1个项二项式定理(binomial theorem)公式特征:2.各项的次数都等于二项式的次数n;3.字母a的次数由n递减到0,字母b的次数由0递增到n.
特别地:若今天是星期五,再过8100天后的那一天是星期几?例题1:练习:必做题:P36 1,2,3作业 布置:小结:知识方面:方法方面:选做题:推导 的展开式。
