解析几何中的最值问题

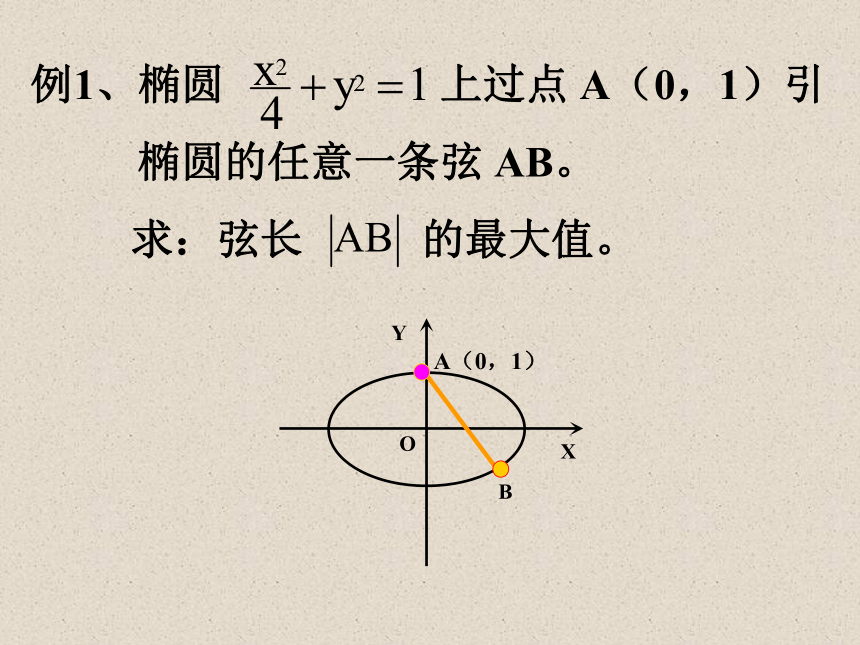
课件20张PPT。解析几何中的最值问题解析几何中求最值问题的基本方法 函数的思想方法 判别式法 利用基本不等式 数形结合 参数法 建立几何模型例1、椭圆 上过点 A（0，1）引
椭圆的任意一条弦 AB。求：弦长 的最大值。设 B（x，y）为椭圆上的一点。设 B（x，y），则 。∵ B（x，y）在椭圆上，代入得：解题思路:把 代入,得出关于 y 的二次函数，
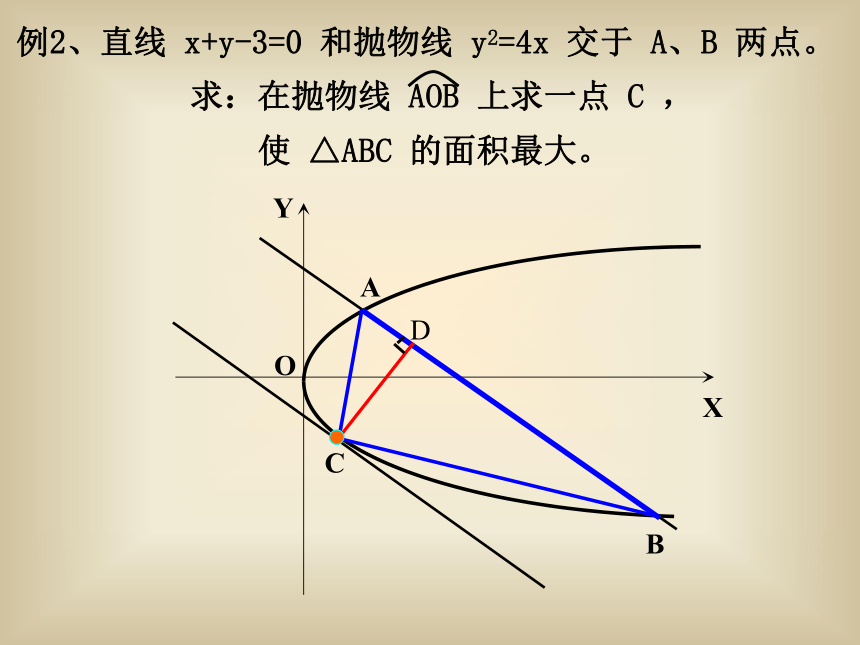
配方后求出的最大值。 解：函数的思想方法例2、直线 x+y-3=0 和抛物线 y2=4x 交于 A、B 两点。
求：在抛物线 AOB 上求一点 C ，
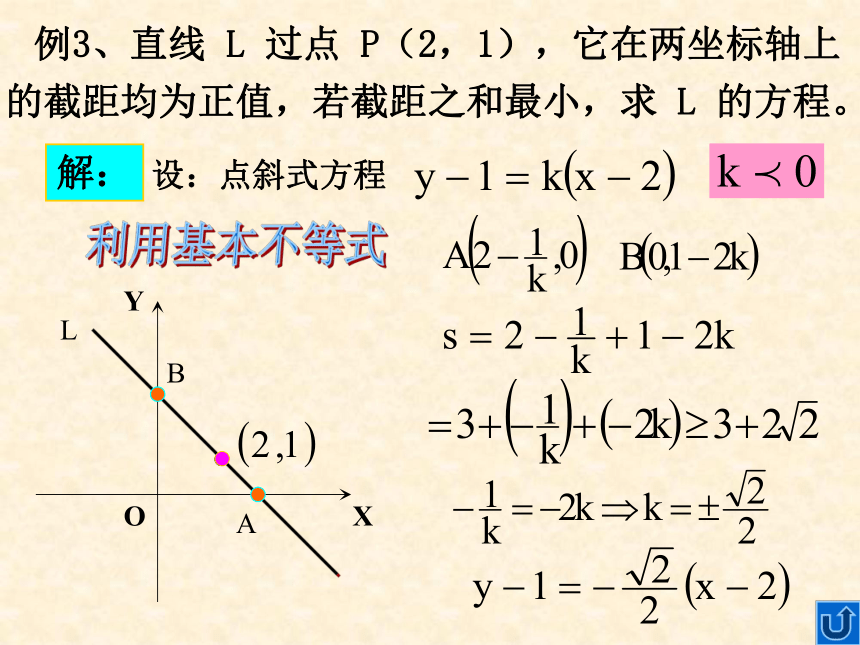
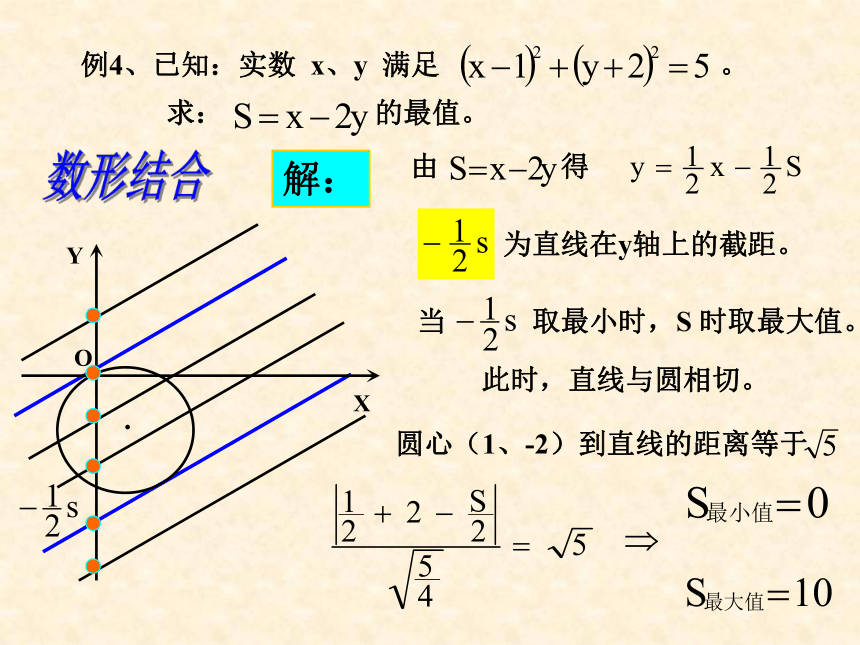
使 △ABC 的面积最大。解方程组解： 判别式法把 m=1 代入得：例3、直线 L 过点 P（2，1），它在两坐标轴上的截距均为正值，若截距之和最小，求 L 的方程。设：点斜式方程解：利用基本不等式例4、已知：实数 x、y 满足 。
求： 的最值。此时，直线与圆相切。由 得
当 取最小时，S 时取最大值。为直线在y轴上的截距。圆心（1、-2）到直线的距离等于解：数形结合例4、已知：实数 x、y 满足 。
求： 的最值。解：将之代入 得：∵Θ∈[0，2π）参数法例5、在直线 x-y+1=0 上找一点 p ，使 p 点到
点 A（1，0）， B（3，0）的距离之和最小。 例5、在直线 x-y+1=0 上找一点 p ，使 p 点到
点 A（1，0）， B（3，0）的距离之和最小。 如图，设 A1（x，y）是点 A 关于直线 x-y+1=0 的对称点。易知：要在直线上找一点 p 到点 A1，B 的距离之和最小，此点应是直线 A1B 与直线的交点。例6、求：使 S 最小的 x 与 y 的值。可设：四个根号的几何意义分别为点P（x，y）到点O（0，0）、A（1、0）、C（0，1）、B（1，1）四点的距离。原来的问题化归为：求到正方形四个顶点距离之和最小的点。分析：由题设的代数结构，联想到平面上两点间的距离。建立几何模型：解：2、已知方程:
求：满足这个方程的实数对（x，y）中， 的最值。练习：用代数方法讨论几何问题是解析几何的特点和手段。对于解析几何中的极值问题的解决首先应注意函数方法（参数法）的运用，将所求对象表示成某个变量的函数，利用代数方法来解决。作为几何中的最值问题，往往利用平面几何知识或图形意义，采取数形结合或不等式的方法求解，可以避开代数形式的复杂运算。反过来，通过建立坐标系，构造图形也可使某些不易处理的代数极值问题得到解决。小结注意！谢谢指导！2、已知方程:
求：满足这个方程的实数对（x，y）中， 的最值。当直线与圆相切时，斜率取到最值。设：解:提示：例、求函数 的最大值。设 y=x2 时 （为抛物线）“抛物线 y=x2 上的动点M（x，y）
到两个定点A（4，3）、B（0，2）
的距离之差的最大值。”易知：思考：建立几何模型：