【必修4课件】2.6平面向量的基本定理及坐标表示
文档属性
| 名称 | 【必修4课件】2.6平面向量的基本定理及坐标表示 |  | |
| 格式 | rar | ||
| 文件大小 | 326.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-10 15:41:00 | ||
图片预览




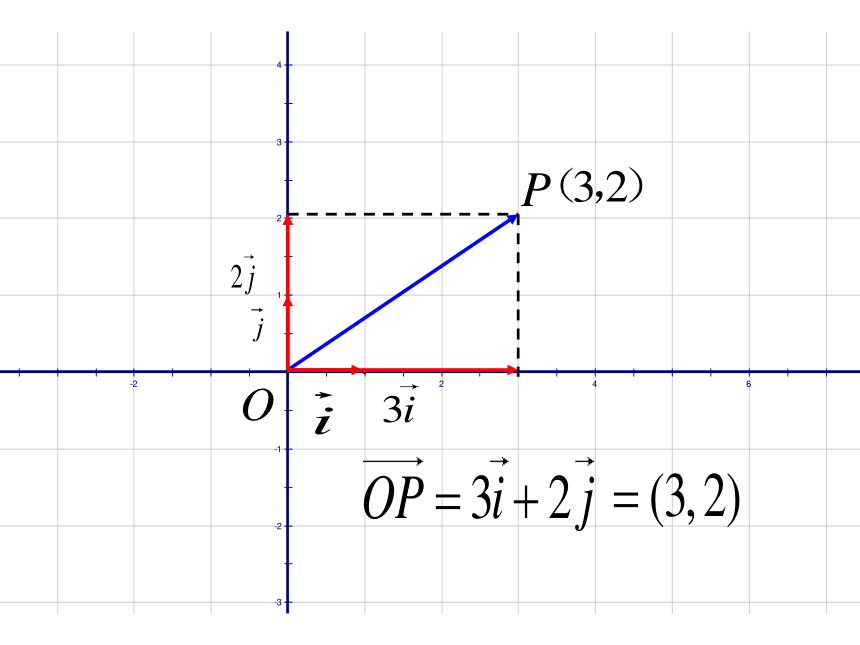
文档简介
课件15张PPT。平面向量的正交分解及坐标表示(可以不同,也可以相同)(有无数对)1.平面向量基本定理 若 e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数 λ1,λ2,使
a=λ1e1+λ2e2.不共线向量e1,e2叫做表示这一平面内所有向量的一组基底. 1.同一平面内可以作基底的向量有多少组?2.不同基底对应向量 a 的表示式是否相同?问题:探究2.平面向量的正交分解及坐标表示 [0°,180°] 1.对于两个非零向量 a 和 b,作OA= a,OB= b,称
∠AOB为向量a与b的夹角.2.如果向量a与b的夹角是90°,则称向量a与b 垂直,记作 a⊥b. 3.把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.4.直角坐标系中,点A的
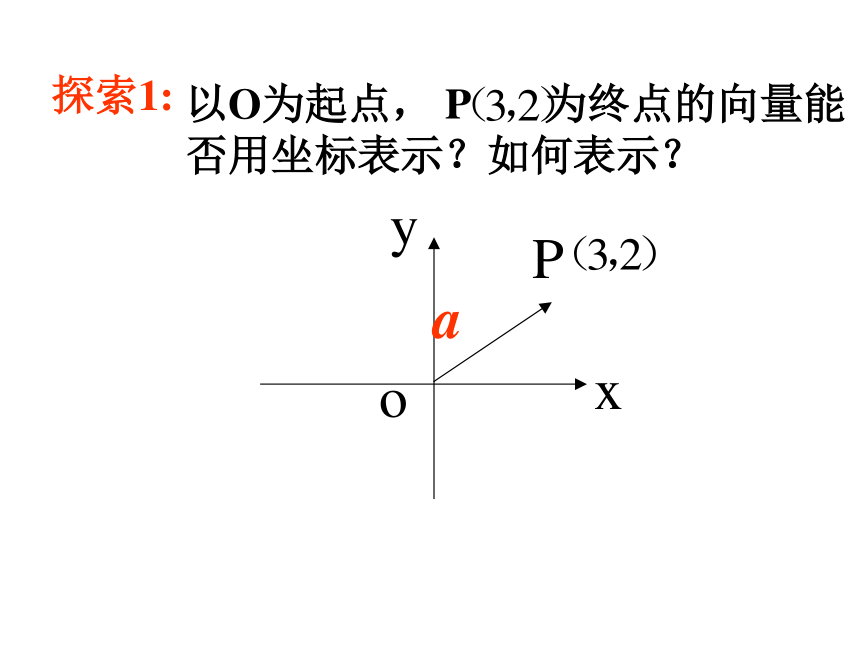
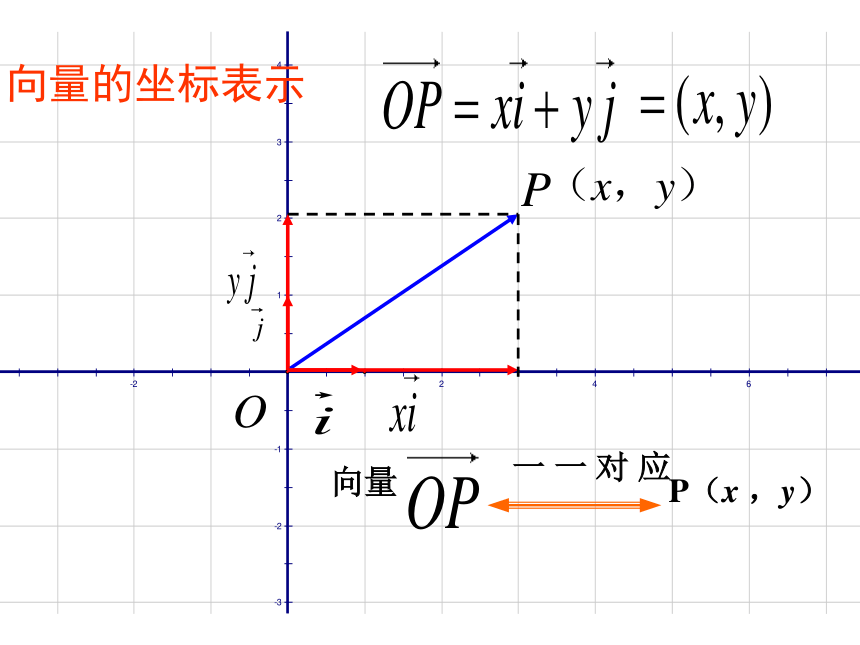
坐标(x ,y)的含义是什么?OM=x,ON=y思考:互相垂直的两个向量能否作为平面内所有向量的一组基底?探索1:以O为起点, P 为终点的向量能否用坐标表示?如何表示?向量的坐标表示4.向量的坐标表示 在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得
a=xi+yj.
有序数对(x,y)叫做向量a的坐标,记作a=(x,y).
其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.平面向量的坐标表示OxyA 在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?探索2: Aoxy 可通过向量的平移,将向量的起点移到坐标的原点O处. 解决方案:例1.如图,分别用基底 , 表示向量 、 、 、 ,并求出
它们的坐标。AA1A2解:如图可知同理 例题报纸 随堂练习 6报纸 随堂练习 2创新 基础测评 1,4创新 课后智能测评 3报纸 同步检测 5
a=λ1e1+λ2e2.不共线向量e1,e2叫做表示这一平面内所有向量的一组基底. 1.同一平面内可以作基底的向量有多少组?2.不同基底对应向量 a 的表示式是否相同?问题:探究2.平面向量的正交分解及坐标表示 [0°,180°] 1.对于两个非零向量 a 和 b,作OA= a,OB= b,称
∠AOB为向量a与b的夹角.2.如果向量a与b的夹角是90°,则称向量a与b 垂直,记作 a⊥b. 3.把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.4.直角坐标系中,点A的
坐标(x ,y)的含义是什么?OM=x,ON=y思考:互相垂直的两个向量能否作为平面内所有向量的一组基底?探索1:以O为起点, P 为终点的向量能否用坐标表示?如何表示?向量的坐标表示4.向量的坐标表示 在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得
a=xi+yj.
有序数对(x,y)叫做向量a的坐标,记作a=(x,y).
其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标.平面向量的坐标表示OxyA 在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?探索2: Aoxy 可通过向量的平移,将向量的起点移到坐标的原点O处. 解决方案:例1.如图,分别用基底 , 表示向量 、 、 、 ,并求出
它们的坐标。AA1A2解:如图可知同理 例题报纸 随堂练习 6报纸 随堂练习 2创新 基础测评 1,4创新 课后智能测评 3报纸 同步检测 5
