(苏忠诚)1.1.3导数的几何意义(2011年3月6日)
文档属性
| 名称 | (苏忠诚)1.1.3导数的几何意义(2011年3月6日) |
|
|
| 格式 | rar | ||
| 文件大小 | 147.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-10 00:00:00 | ||
图片预览





文档简介
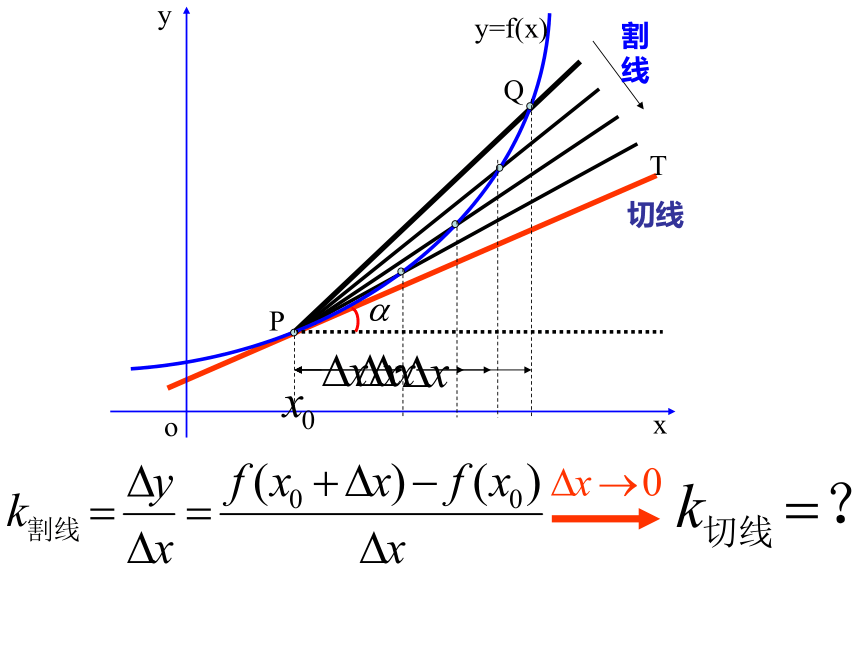
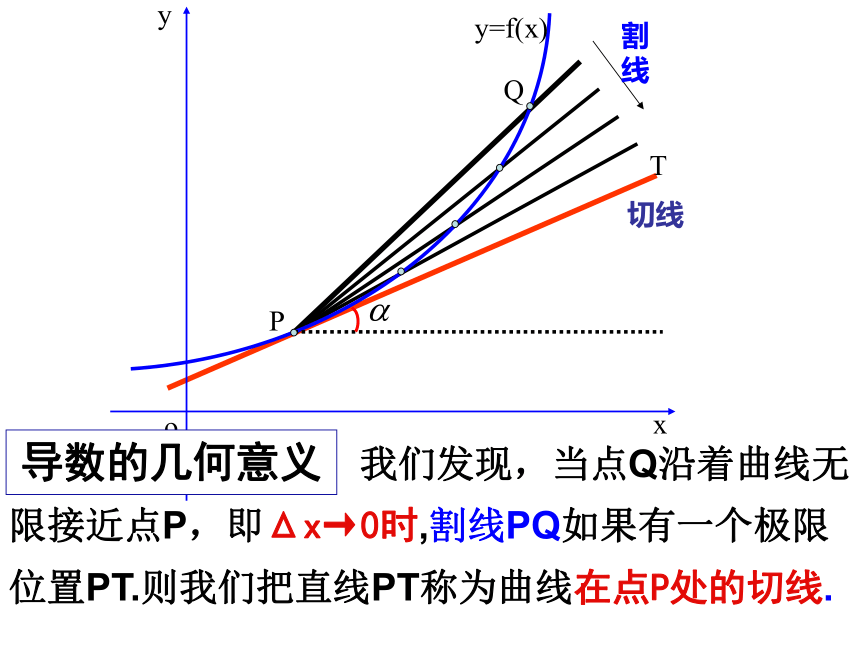
课件18张PPT。1.1.1变化率与导数的概念平均变化率瞬时变化率直线斜率平均速度切线斜率瞬时速度复习:设函数f(x) ,求其在x=x 0 处的导数步骤:注意:这里的增量不是一般意义上的增量,它可正也可负. 自变量的增量Δx的形式是多样的,但不论Δx选择 哪种形式, Δy也必须选择与之相对应的形式.1.1.3导数的几何意义函数f(x)在 处的瞬时变化率。我们知道:导数 表示:反映了函数f(x)在 附近的变化情况。那么:导数 的几何意义是什么呢?PQ割线切线TPQ割线切线T导数的几何意义 我们发现,当点Q沿着曲线无限接近点P,即Δx→0时,割线PQ如果有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.PQoxyy=f(x)割线切线T这个概念:
①提供了求曲线上某点切线的斜率的一种方法; ②切线斜率的本质——函数在x=x0处的导数.要注意,曲线在某点处的切线:
1) 与该点的位置有关;
要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.例题讲解:关注用导数本质及其几何意义解决问题 从求函数f(x)在x=x0处导数的过程可以看到:当x=x0时, 是一个确定的数。即:思考题小结1. 导数的实质: 就是 瞬时变化率;2. 导数的几何意义: 切线的斜率;3. 导数表示了现实生活中事物的发展在某一时刻的瞬时变化发展情况,它的符号刻划变化的增减,它的绝对值反映了变化的快慢;4. 求导数最基本的方法: 由定义求导数.再见
①提供了求曲线上某点切线的斜率的一种方法; ②切线斜率的本质——函数在x=x0处的导数.要注意,曲线在某点处的切线:
1) 与该点的位置有关;
要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;
3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多个.例题讲解:关注用导数本质及其几何意义解决问题 从求函数f(x)在x=x0处导数的过程可以看到:当x=x0时, 是一个确定的数。即:思考题小结1. 导数的实质: 就是 瞬时变化率;2. 导数的几何意义: 切线的斜率;3. 导数表示了现实生活中事物的发展在某一时刻的瞬时变化发展情况,它的符号刻划变化的增减,它的绝对值反映了变化的快慢;4. 求导数最基本的方法: 由定义求导数.再见
