(苏忠诚)1.2.1几个常用函数的导函数(2011年3月8日)
文档属性
| 名称 | (苏忠诚)1.2.1几个常用函数的导函数(2011年3月8日) | 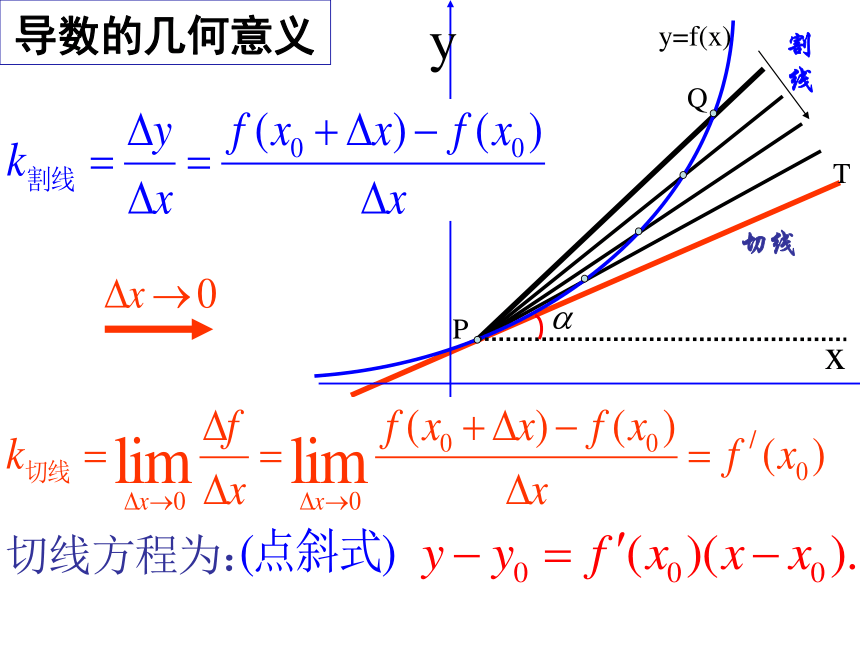 | |
| 格式 | rar | ||
| 文件大小 | 243.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-04-10 15:47:00 | ||
图片预览







文档简介
课件19张PPT。PQoxyy=f(x)割线切线T导数的几何意义设函数f(x) ,求其导函数步骤:二、新课——几种常见函数的导数根据导数的定义可以得出一些常见函数的导数公式.公式1: .1) 函数y=f(x)=c的导数.这说明什么?
请同学们求下列函数的导数:达标训练一1.求下列函数的导数:我们今后可以直接使用的 基本初等函数的导数公式思考回答:达标训练二写出下列函数的导数
y=cosx, y=sinx, y=2x, y=lnx, y=ex新课 导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:巩固性训练求下列函数的导数:
(1)f(x)=a0xn+ a1xn-1+…+an-1x+an
(2)f(x)=x+x-1
(3)f(x)=x2+2cosx
某函数的导函数为 ,则原函数为 。例1.求函数y=x4+2xcosx的导数.例4.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均 相切,求l的方程.解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).对于 则与S1相切于P点的切线方程为y-x12
=2x1(x-x1),即y=2x1x-x12.①对于 与S2相切于Q点的切线方程为y+
(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4.②因为两切线重合,若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.所以所求l的方程为:y=0或y=4x-4..我们今后可以直接使用的 基本初等函数的导数公式小结:导数的四则运算
请同学们求下列函数的导数:达标训练一1.求下列函数的导数:我们今后可以直接使用的 基本初等函数的导数公式思考回答:达标训练二写出下列函数的导数
y=cosx, y=sinx, y=2x, y=lnx, y=ex新课 导数的运算法则:法则1:两个函数的和(差)的导数,等于这两个函数的导数的和(差),即:法则2:两个函数的积的导数,等于第一个函数的导数乘第二个函数,加上第一个函数乘第二个函数的导数 ,即:法则3:两个函数的商的导数,等于第一个函数的导数乘第二个函数,减去第一个函数乘第二个函数的导数 ,再除以第二个函数的平方.即:巩固性训练求下列函数的导数:
(1)f(x)=a0xn+ a1xn-1+…+an-1x+an
(2)f(x)=x+x-1
(3)f(x)=x2+2cosx
某函数的导函数为 ,则原函数为 。例1.求函数y=x4+2xcosx的导数.例4.已知曲线S1:y=x2与S2:y=-(x-2)2,若直线l与S1,S2均 相切,求l的方程.解:设l与S1相切于P(x1,x12),l与S2相切于Q(x2,-(x2-2)2).对于 则与S1相切于P点的切线方程为y-x12
=2x1(x-x1),即y=2x1x-x12.①对于 与S2相切于Q点的切线方程为y+
(x2-2)2=-2(x2-2)(x-x2),即y=-2(x2-2)x+x22-4.②因为两切线重合,若x1=0,x2=2,则l为y=0;若x1=2,x2=0,则l为y=4x-4.所以所求l的方程为:y=0或y=4x-4..我们今后可以直接使用的 基本初等函数的导数公式小结:导数的四则运算
