2.2.2平面与平面平行的判定

课件11张PPT。　　三角板有一条边与平面平行，当三角板怎么放置时，三角板所在的平面与桌面平行？思考：如果平面内有一条直线与平面平行，那么平面是否与平面平行？为什么？ 思考：如果平面内有两条直线与平面平行，那么平面与平面平行吗？为什么？ 两个图形：一个是有两条平行直线与平面平行，
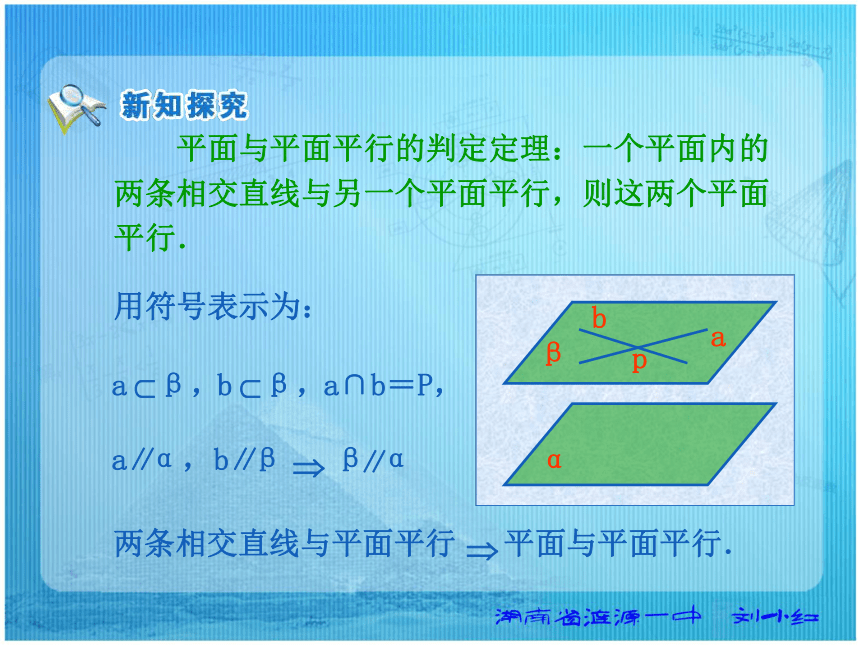
一个是相交直线与平面平行．　　平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行． 用符号表示为：a∩b＝P，T　　判定定理证明两个平面平行，必须满足两个条件：(1)有两条直线平行于同
　 一个平面;(2)这两条直线必须相交．已知正方体ABCD-A1B1C1D1，证明:因为ABCD-A1B1C1D1是正方体， 所以D1C1∥A1B1，又AB∥A1B1，所以D1C1∥AB，所以D1C1BA为平行四边形D1C1=A1B1．AB=A1B1， D1C1=AB．所以D1A∥C1B， 由直线与平面平行的判定定理得： D1A∥平面C1BD，同理：D1B1平面C1BD，又因为D1A∩D1B1=D1，所以平面AB1D1∥平面C1BD． 求证：平面AB1D1∥平面C1BD．　　如图：正方体ABCD-A1B1C1D1中，M，N，E，F
分别是棱A1B1，A1D1，B1C1，C1D1的中点．求证：
平面AMN∥平面EFDB．证明：∵MN∥EF，NA∥EB ∴平面AMN∥平面EFDB平面与平面平行的条件可以是（ ）．A：α内有无穷多条直线都与β平行．B：直线a∥α，a∥β，且直线a不在α内，也　
不在β内． D：α内的任何直线都与β平行． D　　我们现在学习的几何学，是由古
希腊数学家 欧几里德(公无前330—
前275)创立的．他在公元前300年编
写的《几何原本》，2000多年来都被
看作学习几何的标准课本，所以称欧
几里德为几何之父．　　欧几里德汇集了前人的成果，采用前所未有
的独特编写方式，先提出定义、公理、公设，然
后由简到繁地证明了一系列定理，讨论了平面图
形和立体图形，还讨论了整数、分数、比例等等，
完成了《几何原本》这部巨著．