3.2.1直线的点斜式方程
图片预览



文档简介
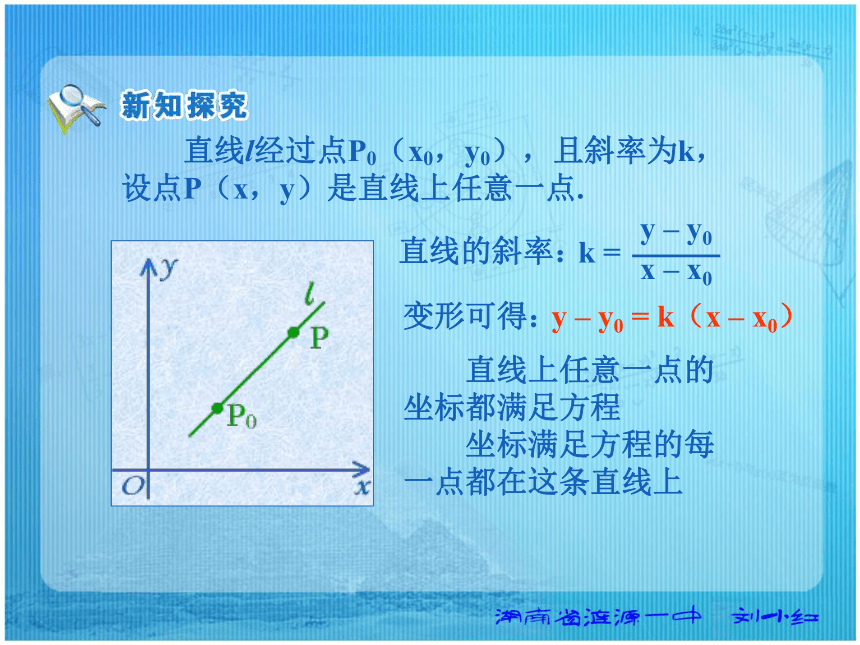
课件19张PPT。 在直角坐标系中,给定一个点P0(x0,y0)
和斜率k,我们能否将直线上所有点的坐标
P(x,y)满足的关系表示出来? 直线l经过点P0(x0,y0),且斜率为k,设点P(x,y)是直线上任意一点.k =直线的斜率:变形可得:y – y0 = k(x – x0) 直线上任意一点的
坐标都满足方程
坐标满足方程的每
一点都在这条直线上 方程y – y0 = k(x – x0)由直线上的一定点及
其斜率确定, 我们把方程y – y0 = k(x – x0)叫做
直线的点斜式方程, 简称点斜式(point slope form) 讨论:直线的点斜式方程能否表示坐标平面
内的所有直线呢?
有斜率的直线才能写成点斜式方程,斜率不
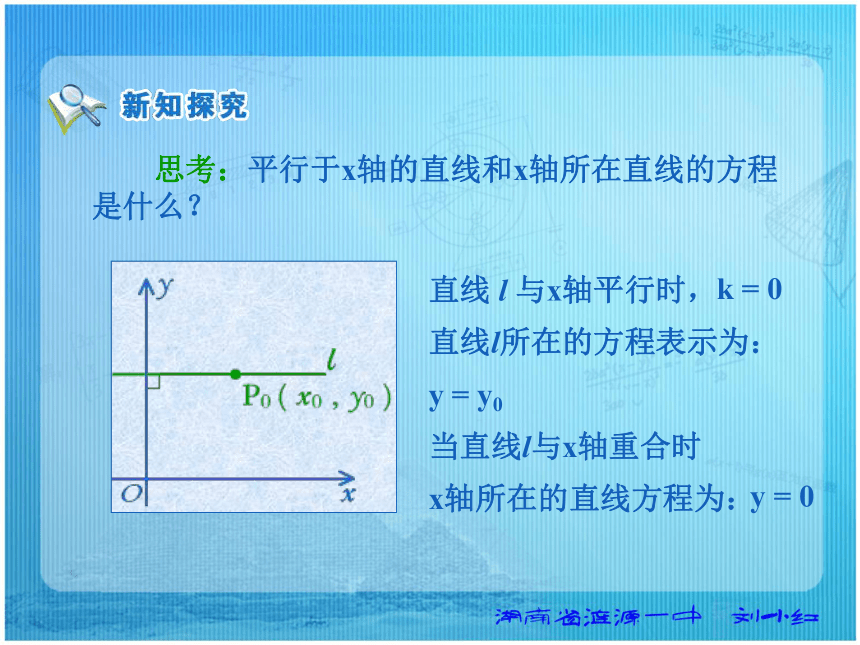
存在的直线,其方程不能用点斜式表示 . 思考:平行于x轴的直线和x轴所在直线的方程是什么? 直线 l 与x轴平行时,
直线l所在的方程表示为:
y = y0
当直线l与x轴重合时
x轴所在的直线方程为:k = 0y = 0 思考:平行于y轴的直线和y轴所在直线的方程
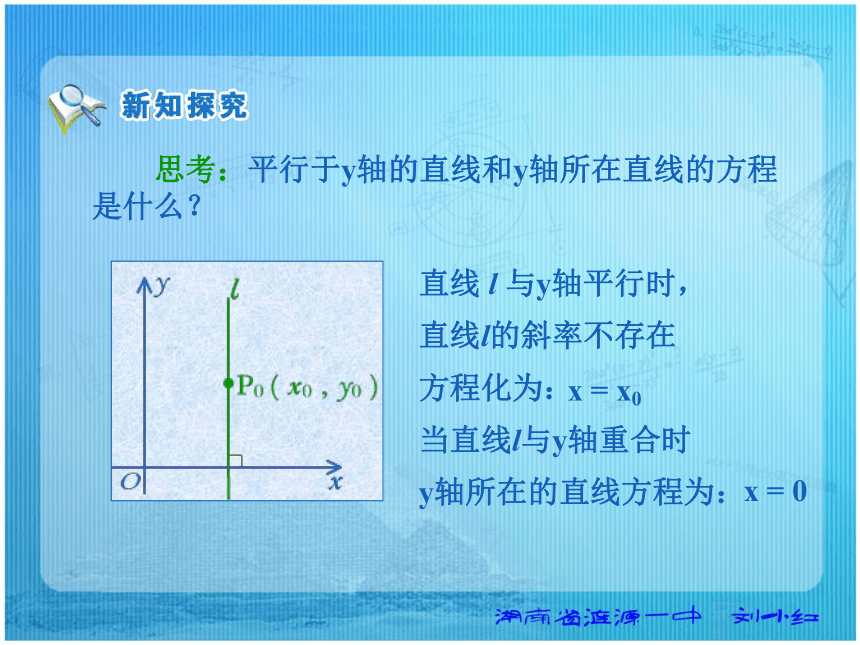
是什么? 直线 l 与y轴平行时,
直线l的斜率不存在
方程化为:
当直线l与y轴重合时
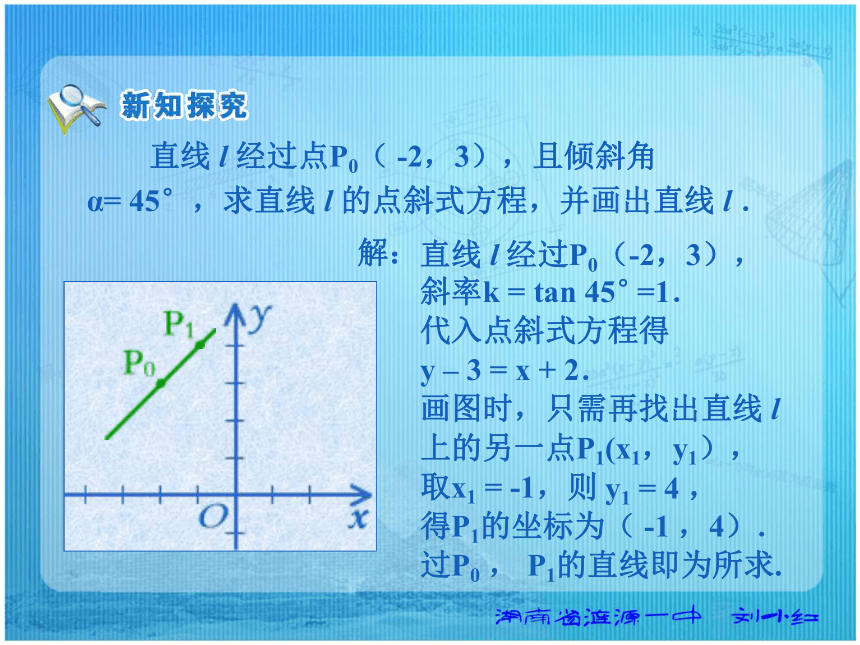
y轴所在的直线方程为:x = x0x = 0 直线 l 经过点P0( -2,3),且倾斜角
α= 45°,求直线 l 的点斜式方程,并画出直线 l .解:
斜率k =
代入点斜式方程得
y – 3 = x + 2.
画图时,只需再找出直线 l
上的另一点P1(x1,y1),
取x1 = -1,则
得P1的坐标为( -1 ,4).
过P0 , P1的直线即为所求.直线 l 经过P0(-2,3),tan 45°=1.y1 = 4 , 直线 l 的斜率为 k,与 y 轴的交点坐标为
(0,b),则直线 l 的方程是什么?代入点斜式方程得:
变形为:y – b = k(x - 0)y = k x + b 我们把直线 l 与 y 轴交点(0,b)的纵坐
标b叫做直线 l 在 y 轴上的截距(intercept)
方程 y = k x + b 叫做直线的斜截式方程,
简称斜截式(slope intercept form) 思考:截距是距离吗?直线在x轴上的截距是
什么? 直线在 y 轴上的截距就是直线与 y 轴交点的纵
坐标.
直线在x轴上的截距是直线与x轴交点的横坐标.
讨论:观察方程 y = x + b ,它的形式具有什么
特点?
方程y = x + b 由直线的斜率与它在 y 轴上的截
距 b确定
y 的系数恒为1, k 为直线的斜率,k 和 b 都有特定的几何意义,b 是直线在y轴上的截距. 已知直线 l1:y = k1 x + b1, l2:y = k2 x + b2;
(1)l1 // l2 的条件是什么?
(2)l1⊥l2的条件是什么? (1)若 l1 // l2,
反之,
(2)若l1⊥l2 ,
反之,
于是我们得到,对于直线:
l1:y = k1 x + b1, l2:y = k2 x + b2,
l1 // l2 ?
l1⊥l2 ? 试讨论:解:则 k1 = k2, 此时 l1,l2 与
y 轴的交点不同,即 b1 ≠ b2 ;k1 = k2,且 b1 ≠ b2 时,l1 // l2 .则k1k2 = - 1 ;k1k2 = - 1 时,l1⊥l2 .k1 = k2 ,且 b1 ≠ b2 ;k1k2= - 1. 写出下列直线的点斜式方程 (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;直线过点(3,-1)解:所以所求直线方程为: 写出下列直线的点斜式方程 (1)经过点A(3,-1),斜率是 ; (2)经过点B(- ,2),倾斜角是30°; (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;解:所以所求直线方程为: 写出下列直线的点斜式方程 (1)经过点A(3,-1),斜率是 ; (2)经过点B(- ,2),倾斜角是30°; (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;解:y - 3 = 0. (3)tan 0°= 0,又因为直线过点(0,3) 即k = 0 所以所求直线方程为: 又因为直线过点(- 4,- 2) 写出下列直线的点斜式方程 (1)经过点A(3,-1),斜率是 ; (2)经过点B(- ,2),倾斜角是30°; (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;解:所以所求直线方程为: (1)已知直线的点斜式方程是y – 2 = x – 1,
那么此直线的斜率是____,倾斜角是____.
(2)已知直线的点斜式方程是
那么此直线的斜率是____,倾斜角是____.145°60°写出下列直线的斜截式方程,并画出直线.(1)斜率是 ,在y轴上的截距是 – 2 ;代入斜截式方程得:b = – 2 ;写出下列直线的斜截式方程,并画出直线.(2)斜率是 – 2 ,在y轴上的截距是 4 .解:(2)由题可知 k = – 2 ,代入斜截式方程得:y = –2 x + 4 b = 4 ;判断下列各对直线是否平行或垂直解:(1)直线 l1 的斜率k1 直线 l2 的斜率k2因为k1 = k2 且 b1 ≠ b2 ;解:(2)直线 l1 的斜率k1 直线 l2 的斜率k2因为k1·k2= – 1,所以 l1 // l2.所以 l1⊥l2. 国庆庆典活动的中心广场有数万名学生手持鲜花组成大型图案方阵,方阵前排距观礼台120米,方阵纵列95人,每列长度192米,问第一、二排间距多大能达到满意的观礼效果
和斜率k,我们能否将直线上所有点的坐标
P(x,y)满足的关系表示出来? 直线l经过点P0(x0,y0),且斜率为k,设点P(x,y)是直线上任意一点.k =直线的斜率:变形可得:y – y0 = k(x – x0) 直线上任意一点的
坐标都满足方程
坐标满足方程的每
一点都在这条直线上 方程y – y0 = k(x – x0)由直线上的一定点及
其斜率确定, 我们把方程y – y0 = k(x – x0)叫做
直线的点斜式方程, 简称点斜式(point slope form) 讨论:直线的点斜式方程能否表示坐标平面
内的所有直线呢?
有斜率的直线才能写成点斜式方程,斜率不
存在的直线,其方程不能用点斜式表示 . 思考:平行于x轴的直线和x轴所在直线的方程是什么? 直线 l 与x轴平行时,
直线l所在的方程表示为:
y = y0
当直线l与x轴重合时
x轴所在的直线方程为:k = 0y = 0 思考:平行于y轴的直线和y轴所在直线的方程
是什么? 直线 l 与y轴平行时,
直线l的斜率不存在
方程化为:
当直线l与y轴重合时
y轴所在的直线方程为:x = x0x = 0 直线 l 经过点P0( -2,3),且倾斜角
α= 45°,求直线 l 的点斜式方程,并画出直线 l .解:
斜率k =
代入点斜式方程得
y – 3 = x + 2.
画图时,只需再找出直线 l
上的另一点P1(x1,y1),
取x1 = -1,则
得P1的坐标为( -1 ,4).
过P0 , P1的直线即为所求.直线 l 经过P0(-2,3),tan 45°=1.y1 = 4 , 直线 l 的斜率为 k,与 y 轴的交点坐标为
(0,b),则直线 l 的方程是什么?代入点斜式方程得:
变形为:y – b = k(x - 0)y = k x + b 我们把直线 l 与 y 轴交点(0,b)的纵坐
标b叫做直线 l 在 y 轴上的截距(intercept)
方程 y = k x + b 叫做直线的斜截式方程,
简称斜截式(slope intercept form) 思考:截距是距离吗?直线在x轴上的截距是
什么? 直线在 y 轴上的截距就是直线与 y 轴交点的纵
坐标.
直线在x轴上的截距是直线与x轴交点的横坐标.
讨论:观察方程 y = x + b ,它的形式具有什么
特点?
方程y = x + b 由直线的斜率与它在 y 轴上的截
距 b确定
y 的系数恒为1, k 为直线的斜率,k 和 b 都有特定的几何意义,b 是直线在y轴上的截距. 已知直线 l1:y = k1 x + b1, l2:y = k2 x + b2;
(1)l1 // l2 的条件是什么?
(2)l1⊥l2的条件是什么? (1)若 l1 // l2,
反之,
(2)若l1⊥l2 ,
反之,
于是我们得到,对于直线:
l1:y = k1 x + b1, l2:y = k2 x + b2,
l1 // l2 ?
l1⊥l2 ? 试讨论:解:则 k1 = k2, 此时 l1,l2 与
y 轴的交点不同,即 b1 ≠ b2 ;k1 = k2,且 b1 ≠ b2 时,l1 // l2 .则k1k2 = - 1 ;k1k2 = - 1 时,l1⊥l2 .k1 = k2 ,且 b1 ≠ b2 ;k1k2= - 1. 写出下列直线的点斜式方程 (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;直线过点(3,-1)解:所以所求直线方程为: 写出下列直线的点斜式方程 (1)经过点A(3,-1),斜率是 ; (2)经过点B(- ,2),倾斜角是30°; (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;解:所以所求直线方程为: 写出下列直线的点斜式方程 (1)经过点A(3,-1),斜率是 ; (2)经过点B(- ,2),倾斜角是30°; (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;解:y - 3 = 0. (3)tan 0°= 0,又因为直线过点(0,3) 即k = 0 所以所求直线方程为: 又因为直线过点(- 4,- 2) 写出下列直线的点斜式方程 (1)经过点A(3,-1),斜率是 ; (2)经过点B(- ,2),倾斜角是30°; (3)经过点C(0,3),倾斜角是0°; (4)经过点D(- 4,- 2),倾斜角是120°;解:所以所求直线方程为: (1)已知直线的点斜式方程是y – 2 = x – 1,
那么此直线的斜率是____,倾斜角是____.
(2)已知直线的点斜式方程是
那么此直线的斜率是____,倾斜角是____.145°60°写出下列直线的斜截式方程,并画出直线.(1)斜率是 ,在y轴上的截距是 – 2 ;代入斜截式方程得:b = – 2 ;写出下列直线的斜截式方程,并画出直线.(2)斜率是 – 2 ,在y轴上的截距是 4 .解:(2)由题可知 k = – 2 ,代入斜截式方程得:y = –2 x + 4 b = 4 ;判断下列各对直线是否平行或垂直解:(1)直线 l1 的斜率k1 直线 l2 的斜率k2因为k1 = k2 且 b1 ≠ b2 ;解:(2)直线 l1 的斜率k1 直线 l2 的斜率k2因为k1·k2= – 1,所以 l1 // l2.所以 l1⊥l2. 国庆庆典活动的中心广场有数万名学生手持鲜花组成大型图案方阵,方阵前排距观礼台120米,方阵纵列95人,每列长度192米,问第一、二排间距多大能达到满意的观礼效果
